Difference between revisions of "Fretting fatigue case"
(→The effect of bulk stress) |
E6WikiAdmin (talk | contribs) |
||
| (20 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| + | {{Box-round|title= Related papers | | ||
| + | [https://e6.ijs.si/ParallelAndDistributedSystems/publications/32424999.pdf G. Kosec, J. Slak, M. Depolli, R. Trobec, K. Pereira, S. Tomar, T. Jacquemin, S. Bordas, M. Wahab; Weak and strong from meshless methods for linear elastic problem under fretting contact conditions, Tribology international, vol. 138, 2019] | ||
| + | |||
| + | [https://e6.ijs.si/ParallelAndDistributedSystems/publications/32230439.pdf J. Slak, G. Kosec; Adaptive radial basis function-generated finite differences method for contact problems, International journal for numerical methods in engineering, vol. 119, 2019 [DOI: 10.1002/nme.6067]] | ||
| + | }} | ||
| + | |||
| + | __TOC__ | ||
| + | |||
Click on [[Solid Mechanics]] to go back. | Click on [[Solid Mechanics]] to go back. | ||
| Line 6: | Line 14: | ||
initiation and propagation lifetime for cylindrical contact configuration, Tribol. Int. 76 (2014) 73–91, doi:10.1016/j.triboint.2014.02.017. </ref> | initiation and propagation lifetime for cylindrical contact configuration, Tribol. Int. 76 (2014) 73–91, doi:10.1016/j.triboint.2014.02.017. </ref> | ||
| + | It is considered within the [http://e6.ijs.si/ParallelAndDistributedSystems/FWO/#home ''' Multi-analysis of fretting fatigue using physical and virtual experiments '''] project | ||
== Contact of cylinders under partial slip == | == Contact of cylinders under partial slip == | ||
| Line 47: | Line 56: | ||
= MLSM numerical solution for FWO case = | = MLSM numerical solution for FWO case = | ||
| − | We replicate the numerical solution described in <ref name="Pereira"></ref> | + | We replicate the numerical solution described in Pereira et al. (2016) <ref name="Pereira"></ref> |
== Case definition == | == Case definition == | ||
We are solving the equation $$(\lambda + \mu) \nabla (\nabla \cdot \b{u}) + \mu \nabla^2 \b{u} = 0$$ | We are solving the equation $$(\lambda + \mu) \nabla (\nabla \cdot \b{u}) + \mu \nabla^2 \b{u} = 0$$ | ||
| − | on the domain $D = [-L/2, L/2] \times [- | + | on the domain $D = [-L/2, L/2] \times [-W/2, 0]$. Componentwise $\b{u} = [u; v]$. |
The boundary conditions are: | The boundary conditions are: | ||
* top: $\vec{t}(x) = (q(x), -p(x))$ or componentwise $\mu \frac{\partial u}{\partial y}(x, 0) + \mu \frac{\partial v}{\partial x}(x, 0) = q(x)$ and $(2 \mu+\lambda) \frac{\partial u}{\partial x}(x, 0) + \lambda \frac{\partial v}{\partial y}(x, 0) = -p(x)$ . | * top: $\vec{t}(x) = (q(x), -p(x))$ or componentwise $\mu \frac{\partial u}{\partial y}(x, 0) + \mu \frac{\partial v}{\partial x}(x, 0) = q(x)$ and $(2 \mu+\lambda) \frac{\partial u}{\partial x}(x, 0) + \lambda \frac{\partial v}{\partial y}(x, 0) = -p(x)$ . | ||
* left: $\b{u} = 0$ or componentwise $u(-L/2, y) = v(-L/2, y) = 0$. | * left: $\b{u} = 0$ or componentwise $u(-L/2, y) = v(-L/2, y) = 0$. | ||
| − | * bottom: up-down symmetry conditions: componentwise $\frac{\partial u}{\partial y}(x, - | + | * bottom: up-down symmetry conditions: componentwise $\frac{\partial u}{\partial y}(x, -W/2) = 0, v(x, -W/2) = 0$. |
| − | * right: this part | + | * right: this part has traction $\sigma_{ax}$, ie. $\vec{t}(y) = \sigma_{ax}\vec{\imath}$ or componentwise $(2 \mu+\lambda) \frac{\partial v}{\partial y}(L/2, y) + \lambda \frac{\partial u}{\partial x}(L/2, y) = 0$ and $\mu \frac{\partial u}{\partial y}(L/2, y) + \mu \frac{\partial v}{\partial x}(L/2, y) = \sigma_{ax}$. |
Illustration of the computational domain is presented below. | Illustration of the computational domain is presented below. | ||
| − | [[File:fwo_bc.png| | + | [[File:fwo_bc.png|800px]] |
| + | |||
| + | <!-- [[File:Screenshot_20171003_083231.png|800px]] --> | ||
== Phsyical parameters == | == Phsyical parameters == | ||
| Line 67: | Line 78: | ||
* $E = \unit{72.1}{GPa}$, Youngs modulus | * $E = \unit{72.1}{GPa}$, Youngs modulus | ||
* $\nu = 0.33$, Poissons ratio | * $\nu = 0.33$, Poissons ratio | ||
| − | * $L = \unit{40}{mm}$, length, width of the pad | + | * $L = \unit{40}{mm}$, length of the pad |
| − | * $ | + | * $W = \unit{10}{mm}$, width of the pad |
| + | * $t = \unit{4}{mm}$, thickness of the pad | ||
* $\sigma_{ax} = \unit{100}{MPa}$, axial pressure | * $\sigma_{ax} = \unit{100}{MPa}$, axial pressure | ||
* $F = \unit{543}{N}$, normal force | * $F = \unit{543}{N}$, normal force | ||
| Line 77: | Line 89: | ||
Derived parameters are, for choice of $R = \unit{10}{mm}$ and $\mu = 0.3$: | Derived parameters are, for choice of $R = \unit{10}{mm}$ and $\mu = 0.3$: | ||
* $E^\ast = \frac{E}{2(1-\nu^2)} = \unit{40.4}{GPa}$, combined Young's modulus | * $E^\ast = \frac{E}{2(1-\nu^2)} = \unit{40.4}{GPa}$, combined Young's modulus | ||
| − | * $p_{max} = p_0 = \sqrt{\frac{FE^\ast}{ | + | * $p_{max} = p_0 = \sqrt{\frac{FE^\ast}{t R \pi}} = \unit{418.10407}{MPa}$, maximal normal pressure |
| − | * $a = 2 \sqrt{\frac{FR}{ | + | * $a = 2 \sqrt{\frac{FR}{t E^\ast \pi}} = \unit{0.2067}{mm}$, semi contact width, contact region is $[-a, a] \times \{0\}$ |
* $c = a \sqrt{1 - \frac{Q}{\mu F}} = \unit{0.04504}{mm}$, stick zone semi width | * $c = a \sqrt{1 - \frac{Q}{\mu F}} = \unit{0.04504}{mm}$, stick zone semi width | ||
* $e = \frac{a \sigma_{ax}}{4 \mu p_{max}} = \unit{0.041197}{mm}$, eccentricity due to axial load | * $e = \frac{a \sigma_{ax}}{4 \mu p_{max}} = \unit{0.041197}{mm}$, eccentricity due to axial load | ||
| Line 86: | Line 98: | ||
Comparison of this solution against FEM solution published in Pereira et al. (2016) is presented below. | Comparison of this solution against FEM solution published in Pereira et al. (2016) is presented below. | ||
| − | [[File: | + | [[File:fwo_cases1.png|800px]] |
| + | |||
| + | Meshes for this plot: [[:File:fwo_meshes.zip]] | ||
| + | |||
| + | Data for this plot: [[:File:fwo_cases_plotdata.mat]] | ||
| + | |||
| + | Script for this plot: [[:File:plot_fwo_cases.m]] | ||
| + | |||
| + | For faster testing, smaller meshes and corresponding solutions are presented below: | ||
| + | |||
| + | [[File:fwo_cases_small_mesh.png|800px]] | ||
| + | |||
| + | Meshes for this plot: [[:File:fwo_small_meshes.zip]] | ||
| + | |||
| + | Data for this plot: [[:File:fwo_cases_small_mesh_plodata.mat]] | ||
| + | |||
| + | Script is the same as above. | ||
| + | |||
| − | |||
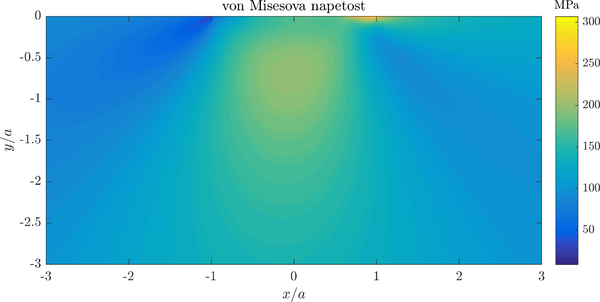
| − | A contour plot of von Mises stress in the specimen is presented below. | + | A contour plot of von Mises stress in the specimen for the case $\mu = 0.65, R = 50$ is presented below. Countour plots for all cases look similar. |
[[File:fwo_solution.png|600px]] | [[File:fwo_solution.png|600px]] | ||
Latest revision as of 18:36, 5 December 2022
Related papers
Contents
Click on Solid Mechanics to go back.
Theoretical introdution
This case is an extension of the classical Hertzian contact, as defined in Pereira et al. (2016) [1] and described in detail in Hojjati-Talemi et al. (2014) [2]
It is considered within the Multi-analysis of fretting fatigue using physical and virtual experiments project
Contact of cylinders under partial slip
This extends the classical theory of Hertzian contact with a tangential force $Q$. When the tangential force is less than the limiting force of friction, i.e., \[|Q| < \mu P,\] where $\mu$ is the coefficent of friction, sliding motion will not occur but the contact will be divided into regions of slip and stick zones that are unknown a priori. For the case of cylinders the analysis is given in Hills & Nowell (1994), p. 44.
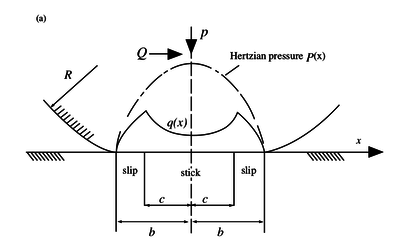
Besides the normal traction $p(x)$ we know have an additional shear traction given by \begin{equation} q(x) = \begin{cases} -\mu p_0 \sqrt{1 - \frac{x^2}{b^2}}, & c \leq |x| \leq b \\ -\mu p_0 \left(\sqrt{1 - \frac{x^2}{b^2}} - \frac{c}{b}\sqrt{1 - \frac{x^2}{c^2}}\right), & |x| < c \end{cases} \end{equation} where $b$ is the half-width of the whole contact, and $c$ the half-width of the central sticking region. The width of the central zone, i.e. the value of dimension $c$ is dependent on the applied tangential force $Q$: \begin{equation} \frac{c}{b} = \sqrt{1 - \frac{Q}{\mu P}} \end{equation}
The distributions $q(x)$ and $p(x)$ as well as the widths of the stick and slip zones can be seen in the image below.
The effect of bulk stress
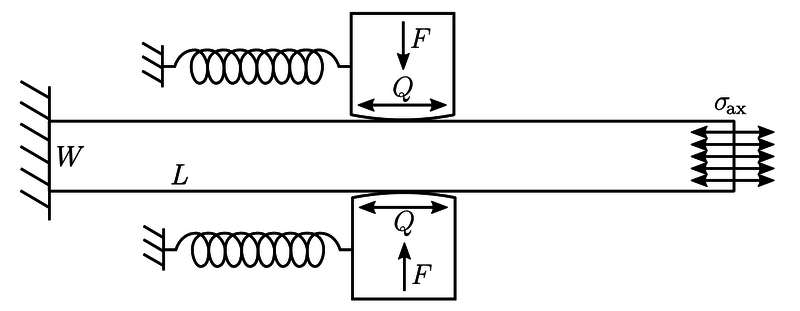
Additionally we might be interested in the addition of bulk stress $\sigma_{\textrm{ax}}$. This type of stress occurs in fretting fatique experiments like the one shown below [1].
The previous solution for contact of cylinders under partial slip can be adjusted for the presence of bulk stresses $\sigma_\mathrm{ax}$. These cause an eccentricity $e$ to the solution given above. The shear traction $q(x)$ can be written as: \begin{equation} q(x) = \begin{cases} -\mu p_0 \sqrt{1 - \frac{x^2}{b^2}}, \quad c \leq | x - e | \text{ and } |x| \leq b \\ -\mu p_0 \left[\sqrt{1 - \frac{x^2}{b^2}} - \frac{c}{b}\sqrt{1 - \frac{(x-e)^2}{c^2}}\right], \quad |x-e| < c \end{cases} \end{equation} where once again \[ \frac{c}{b} = \sqrt{1 - \frac{Q}{\mu F}}\] and \begin{equation} e = \frac{b \sigma_\mathrm{ax}}{4 \mu p_0}. \end{equation} If larger values of $\sigma_\mathrm{ax}$ are applied, one edge of the stick zone will approach the edge of the contact ($e$ becomes larger). The solution for the shear stress traction is therefore only valid if $e + c \leq b$, i. e. \[\frac{\sigma_\mathrm{ax}}{\mu p_0} \leq 4\left(1 - \sqrt{1 - \frac{Q}{\mu F}}\right).\]
MLSM numerical solution for FWO case
We replicate the numerical solution described in Pereira et al. (2016) [1]
Case definition
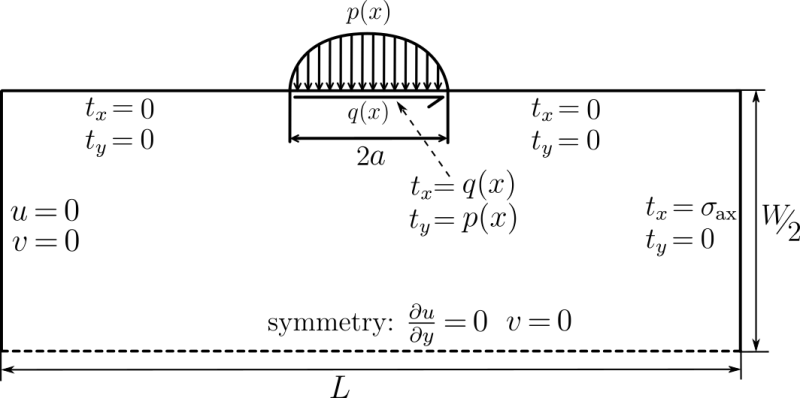
We are solving the equation $$(\lambda + \mu) \nabla (\nabla \cdot \b{u}) + \mu \nabla^2 \b{u} = 0$$ on the domain $D = [-L/2, L/2] \times [-W/2, 0]$. Componentwise $\b{u} = [u; v]$. The boundary conditions are:
- top: $\vec{t}(x) = (q(x), -p(x))$ or componentwise $\mu \frac{\partial u}{\partial y}(x, 0) + \mu \frac{\partial v}{\partial x}(x, 0) = q(x)$ and $(2 \mu+\lambda) \frac{\partial u}{\partial x}(x, 0) + \lambda \frac{\partial v}{\partial y}(x, 0) = -p(x)$ .
- left: $\b{u} = 0$ or componentwise $u(-L/2, y) = v(-L/2, y) = 0$.
- bottom: up-down symmetry conditions: componentwise $\frac{\partial u}{\partial y}(x, -W/2) = 0, v(x, -W/2) = 0$.
- right: this part has traction $\sigma_{ax}$, ie. $\vec{t}(y) = \sigma_{ax}\vec{\imath}$ or componentwise $(2 \mu+\lambda) \frac{\partial v}{\partial y}(L/2, y) + \lambda \frac{\partial u}{\partial x}(L/2, y) = 0$ and $\mu \frac{\partial u}{\partial y}(L/2, y) + \mu \frac{\partial v}{\partial x}(L/2, y) = \sigma_{ax}$.
Illustration of the computational domain is presented below.
Phsyical parameters
Basic parameters are:
- $E = \unit{72.1}{GPa}$, Youngs modulus
- $\nu = 0.33$, Poissons ratio
- $L = \unit{40}{mm}$, length of the pad
- $W = \unit{10}{mm}$, width of the pad
- $t = \unit{4}{mm}$, thickness of the pad
- $\sigma_{ax} = \unit{100}{MPa}$, axial pressure
- $F = \unit{543}{N}$, normal force
- $Q = \unit{155}{N}$, tangential force
- $R = \unit{10}{mm}$ or $\unit{50}{mm}$, raduis of curvature of the cylindrical pad
- $COF = \mu = 0.3$ or $0.85$ or $2$, coefficient of friction
Derived parameters are, for choice of $R = \unit{10}{mm}$ and $\mu = 0.3$:
- $E^\ast = \frac{E}{2(1-\nu^2)} = \unit{40.4}{GPa}$, combined Young's modulus
- $p_{max} = p_0 = \sqrt{\frac{FE^\ast}{t R \pi}} = \unit{418.10407}{MPa}$, maximal normal pressure
- $a = 2 \sqrt{\frac{FR}{t E^\ast \pi}} = \unit{0.2067}{mm}$, semi contact width, contact region is $[-a, a] \times \{0\}$
- $c = a \sqrt{1 - \frac{Q}{\mu F}} = \unit{0.04504}{mm}$, stick zone semi width
- $e = \frac{a \sigma_{ax}}{4 \mu p_{max}} = \unit{0.041197}{mm}$, eccentricity due to axial load
Numerical solution
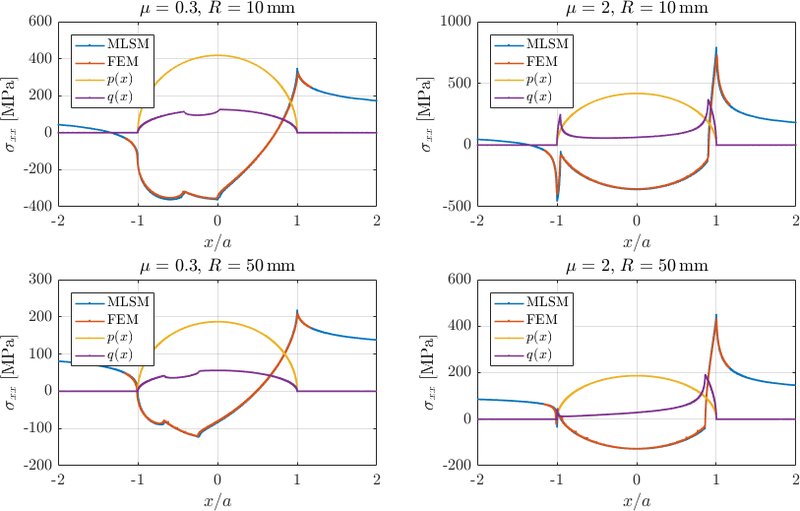
Comparison of this solution against FEM solution published in Pereira et al. (2016) is presented below.
Meshes for this plot: File:fwo_meshes.zip
Data for this plot: File:fwo_cases_plotdata.mat
Script for this plot: File:plot_fwo_cases.m
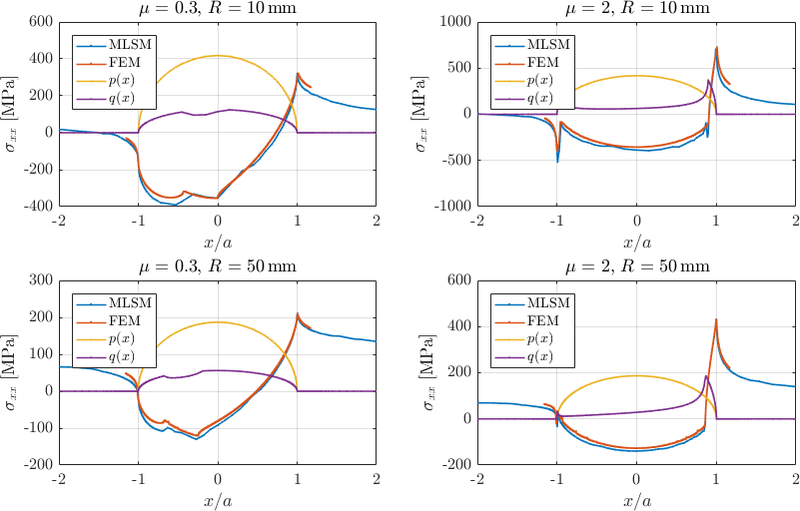
For faster testing, smaller meshes and corresponding solutions are presented below:
Meshes for this plot: File:fwo_small_meshes.zip
Data for this plot: File:fwo_cases_small_mesh_plodata.mat
Script is the same as above.
A contour plot of von Mises stress in the specimen for the case $\mu = 0.65, R = 50$ is presented below. Countour plots for all cases look similar.
Note that contour of stress are similar to the ones in Hertzian contact above, but a significant concentracion of stresses under the contact area is present.
References
- ↑ 1.0 1.1 1.2 K. Pereira et al., On the convergence of stresses in fretting fatigue, Materials 9(8) (2016), doi:10.3390/ma9080639
- ↑ R. Hojjati-Talemi, M. A. Wahab in dr., Prediction of fretting fatigue crack initiation and propagation lifetime for cylindrical contact configuration, Tribol. Int. 76 (2014) 73–91, doi:10.1016/j.triboint.2014.02.017.