Difference between revisions of "Weighted Least Squares (WLS)"
(→Method description) |
(→Method description) |
||
| Line 12: | Line 12: | ||
In general, an approximation function around point $p\in\R^k$ can be | In general, an approximation function around point $p\in\R^k$ can be | ||
written as \[\hat{u} (p) = \sum_{i=1}^m \alpha_i b_i(p) = \b{b}(p)^\T \b{\alpha} \] | written as \[\hat{u} (p) = \sum_{i=1}^m \alpha_i b_i(p) = \b{b}(p)^\T \b{\alpha} \] | ||
| − | where $\b{b} = (b_i)_{i=1}^m$ is a set of ''basis functions'', and $\b{\alpha} = (\alpha_i)_{i=1}^m$ are the unknown coefficients. | + | where $\b{b} = (b_i)_{i=1}^m$ is a set of ''basis functions'', $b_i\colon \r^k \to\R$, and $\b{\alpha} = (\alpha_i)_{i=1}^m$ are the unknown coefficients. |
In MLS the goal is to minimize the error of approximation in given values, $\b{e} = \hat u(\b{x}) - \b{u}$ | In MLS the goal is to minimize the error of approximation in given values, $\b{e} = \hat u(\b{x}) - \b{u}$ | ||
| − | between the approximation function and target function in the known points $\b{x}$. | + | between the approximation function and target function in the known points $\b{x}$. The error can also be written as $B\b{\alpha} - \b{u}$, |
| + | where $B$ is rectangular matrix of dimensions $n \times m$ with rows containing basis function evaluated in points $x_j$. | ||
| + | \[ B = | ||
| + | \begin{bmatrix} | ||
| + | b_1(x_1) & \ldots & b_m(x_1) \\ | ||
| + | \vdots & \ddots & \vdots \\ | ||
| + | b_1(x_n) & \ldots & b_m(x_n) | ||
| + | \end{bmatrix} = | ||
| + | [b_i(x_j)]_{i=1,j=1}^{m,n} = [\b{b}(x_j)^\T]_{j=1}^n. \] | ||
| + | The matrix $B$ is called a ''colocation matrix'' and the problem is called ''correct'' if $B$ is of full rank. | ||
| + | |||
| + | We can choose to minimize any norm of the error vector $e$ | ||
and usually choose to minimize the 2-norm or square norm \[ \|\b{e}\| = \|\b{e}\|_2 = \sqrt{\sum_{j=1}^n e_j^2}. \] | and usually choose to minimize the 2-norm or square norm \[ \|\b{e}\| = \|\b{e}\|_2 = \sqrt{\sum_{j=1}^n e_j^2}. \] | ||
Commonly, we also choose to minimize a weighted norm | Commonly, we also choose to minimize a weighted norm | ||
| Line 30: | Line 41: | ||
A choice of minimizing the square norm gave this method its name -- Least Squares appoximation. If we use the weighted version, we get the Weighted Least Squares or WLS. | A choice of minimizing the square norm gave this method its name -- Least Squares appoximation. If we use the weighted version, we get the Weighted Least Squares or WLS. | ||
In the most general case we wish to minimize | In the most general case we wish to minimize | ||
| − | \[ \|\b{e}\|_{2,w} | + | \[ \|\b{e}\|_{2,w}^2 = \b{e}^\T W^2 \b{e} = (B\b{\alpha} - \b{u})^\T W^2(B\b{\alpha} - \b{u}) = \sum_j^n w_j^2 (\hat{u}(x_j) - u_j)^2 \] |
| − | |||
| − | |||
| − | * Normal | + | The least squares problem can be solved with at least three approaches: |
| + | * Normal equations (fastest - less accurate) - using Cholesky decomposition | ||
* QR decomposition of $\b{B}$ ($rank(\b{B})=m$ - number of basis functions) | * QR decomposition of $\b{B}$ ($rank(\b{B})=m$ - number of basis functions) | ||
* SVD decomposition of $\b{B}$ (more expensive - more reliable, no rank demand) | * SVD decomposition of $\b{B}$ (more expensive - more reliable, no rank demand) | ||
Revision as of 00:30, 24 October 2016
One of the most important building blocks of the meshless methods is the Moving Least Squares approximation, which is implemented in the EngineMLS class. Check EngineMLS unit tests for examples.
Method description
Our wish is to approximate an unknown function $u\colon \R^k \to \R$ while knowing $n$ values $u(x_j) := u_j$. The vector of known values will be denoted by $\b{u}$ and the vector of coordinates where those values were achieved by $\b{x}$. Note that $\b{x}$ is not a vector in the usual sense since its components $x_j$ are elements of $\R^k$, but we will call it vector anyway. The values of $\b{x}$ are called nodes or support nodes or support. The known values $\bf{u}$ are also called support values.
In general, an approximation function around point $p\in\R^k$ can be written as \[\hat{u} (p) = \sum_{i=1}^m \alpha_i b_i(p) = \b{b}(p)^\T \b{\alpha} \] where $\b{b} = (b_i)_{i=1}^m$ is a set of basis functions, $b_i\colon \r^k \to\R$, and $\b{\alpha} = (\alpha_i)_{i=1}^m$ are the unknown coefficients.
In MLS the goal is to minimize the error of approximation in given values, $\b{e} = \hat u(\b{x}) - \b{u}$ between the approximation function and target function in the known points $\b{x}$. The error can also be written as $B\b{\alpha} - \b{u}$, where $B$ is rectangular matrix of dimensions $n \times m$ with rows containing basis function evaluated in points $x_j$. \[ B = \begin{bmatrix} b_1(x_1) & \ldots & b_m(x_1) \\ \vdots & \ddots & \vdots \\ b_1(x_n) & \ldots & b_m(x_n) \end{bmatrix} = [b_i(x_j)]_{i=1,j=1}^{m,n} = [\b{b}(x_j)^\T]_{j=1}^n. \] The matrix $B$ is called a colocation matrix and the problem is called correct if $B$ is of full rank.
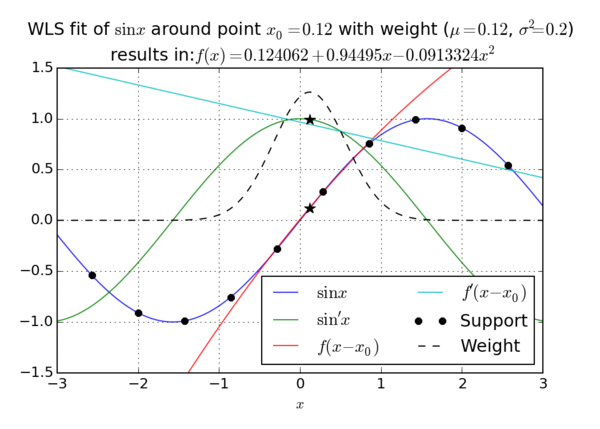
We can choose to minimize any norm of the error vector $e$ and usually choose to minimize the 2-norm or square norm \[ \|\b{e}\| = \|\b{e}\|_2 = \sqrt{\sum_{j=1}^n e_j^2}. \] Commonly, we also choose to minimize a weighted norm [1] instead \[ \|\b{e}\|_{2,w} = \|\b{e}\|_w = \sqrt{\sum_{j=1}^n (w_j e_j)^2}. \] The weights $w_i$ are assumed to be non negative and are assembled in a vector $\b{w}$ or a matrix $W = \operatorname{diag}(\b{w})$ and usually obtained from a weight function. A weight function is a function $\omega\colon \R^k \to[0,\infty)$. We calculate $w_j$ as $w_i := \omega(p-x_j)$, so good choices for $\omega$ are function which have higher values close to 0 (making closer nodes more important), like the normal distribution. If we choose $\omega \equiv 1$, we get the unweighted version.
A choice of minimizing the square norm gave this method its name -- Least Squares appoximation. If we use the weighted version, we get the Weighted Least Squares or WLS. In the most general case we wish to minimize \[ \|\b{e}\|_{2,w}^2 = \b{e}^\T W^2 \b{e} = (B\b{\alpha} - \b{u})^\T W^2(B\b{\alpha} - \b{u}) = \sum_j^n w_j^2 (\hat{u}(x_j) - u_j)^2 \]
The least squares problem can be solved with at least three approaches:
- Normal equations (fastest - less accurate) - using Cholesky decomposition
- QR decomposition of $\b{B}$ ($rank(\b{B})=m$ - number of basis functions)
- SVD decomposition of $\b{B}$ (more expensive - more reliable, no rank demand)
In MM we use SVD.
Normal equations
We seek the minimum of \[{r^2} = {\left( {{\bf{u}} - {\bf{B\alpha }}} \right)^{\rm{T}}}\left( {{\bf{u}} - {\bf{B\alpha }}} \right)\] By seeking the zero gradient in terms of coefficient \[\frac{\partial }{{\partial {\alpha _i}}}\left( {{{\left( {{\bf{u}} - {\bf{B\alpha }}} \right)}^{\rm{T}}}\left( {{\bf{u}} - {\bf{B\alpha }}} \right)} \right) = 0\] resulting in \[{\bf{B}}{{\bf{B}}^{\rm{T}}}{\bf{\alpha }} = {{\bf{B}}^{\rm{T}}}{\bf{u}}\] The coefficient matrix $\bf{B}^T\bf{B}$ is symmetric and positive definite. However, solving above problem directly is poorly behaved with respect to round-off effects since the condition number of $\bf{B}^T\bf{B}$ is the square of that of $\bf{B}$. Or in case of weighted LS \[{\bf{WB}}{{\bf{B}}^{\rm{T}}}{\bf{\alpha }} = {\bf{W}}{{\bf{B}}^{\rm{T}}}{\bf{u}}\]
Complexity of Cholesky decomposition is $\frac{{{n}^{3}}}{3}$ and complexity of matrix multiplication $n{{m}^{2}}$
Pros: simple to implement, low computational complexity Cons: unstable
QR Decomposition
\[{\bf{B}} = {\bf{QR}} = \left[ {{{\bf{Q}}_1},{{\bf{Q}}_2}} \right]\left[ {\begin{array}{*{20}{c}} {{{\bf{R}}_1}}\\ 0 \end{array}} \right]\] \[{\bf{B}} = {{\bf{Q}}_1}{{\bf{R}}_1}\] $\bf{Q}$ is unitary matrix ($\bf{Q}^{-1}=\bf{Q}^T$). Useful property of a unitary matrices is that multiplying with them does not alter the (Euclidean) norm of a vector, i.e., \[\left\| {{\bf{Qx}}} \right\|{\bf{ = }}\left\| {\bf{x}} \right\|\] And $\bf{R}$ is upper diagonal matrix \[{\bf{R = (}}{{\bf{R}}_{\bf{1}}}{\bf{,}}0{\bf{)}}\] therefore we can say \[\begin{array}{l} \left\| {{\bf{B\alpha }} - {\bf{u}}} \right\| = \left\| {{{\bf{Q}}^{\rm{T}}}\left( {{\bf{B\alpha }} - {\bf{u}}} \right)} \right\| = \left\| {{{\bf{Q}}^{\rm{T}}}{\bf{B\alpha }} - {{\bf{Q}}^{\rm{T}}}{\bf{u}}} \right\|\\ = \left\| {{{\bf{Q}}^{\rm{T}}}\left( {{\bf{QR}}} \right){\bf{\alpha }} - {{\bf{Q}}^{\rm{T}}}{\bf{u}}} \right\| = \left\| {\left( {{{\bf{R}}_1},0} \right){\bf{\alpha }} - {{\left( {{{\bf{Q}}_1},{{\bf{Q}}_{\bf{2}}}} \right)}^{\rm{T}}}{\bf{u}}} \right\|\\ = \left\| {{{\bf{R}}_{\bf{1}}}{\bf{\alpha }} - {{\bf{Q}}_{\bf{1}}}{\bf{u}}} \right\| + \left\| {{\bf{Q}}_2^{\rm{T}}{\bf{u}}} \right\| \end{array}\] Of the two terms on the right we have no control over the second, and we can render the first one zero by solving \[{{\bf{R}}_{\bf{1}}}{\bf{\alpha }} = {\bf{Q}}_{_{\bf{1}}}^{\rm{T}}{\bf{u}}\] Which results in a minimum. We could also compute it with pseudo inverse \[\mathbf{\alpha }={{\mathbf{B}}^{-1}}\mathbf{u}\] Where pseudo inverse is simply \[{{\mathbf{B}}^{-1}}=\mathbf{R}_{\text{1}}^{\text{-1}}{{\mathbf{Q}}^{\text{T}}}\] (once again, R is upper diagonal matrix, and Q is unitary matrix). And for weighted case \[\mathbf{\alpha }={{\left( {{\mathbf{W}}^{0.5}}\mathbf{B} \right)}^{-1}}\left( {{\mathbf{W}}^{0.5}}\mathbf{u} \right)\]
Complexity of QR decomposition \[\frac{2}{3}m{{n}^{2}}+{{n}^{2}}+\frac{1}{3}n-2=O({{n}^{3}})\]
Pros: better stability in comparison with normal equations cons: higher complexity
SVD decomposition
In linear algebra, the singular value decomposition (SVD) is a factorization of a real or complex matrix. It has many useful applications in signal processing and statistics.
Formally, the singular value decomposition of an $m \times n$ real or complex matrix $\bf{B}$ is a factorization of the form $\bf{B}= \bf{U\Sigma V^\T}$, where $\bf{U}$ is an $m \times m$ real or complex unitary matrix, $\bf{\Sigma}$ is an $m \times n$ rectangular diagonal matrix with non-negative real numbers on the diagonal, and $\bf{V}^\T$ is an $n \times n$ real or complex unitary matrix. The diagonal entries $\Sigma_{ii}$ are known as the singular values of $\bf{B}$. The $m$ columns of $\bf{U}$ and the $n$ columns of $\bf{V}$ are called the left-singular vectors and right-singular vectors of $\bf{B}$, respectively.
The singular value decomposition and the eigen decomposition are closely related. Namely:
- The left-singular vectors of $\bf{B}$ are eigen vectors of $\bf{BB}^\T$.
- The right-singular vectors of $\bf{B}$ are eigen vectors of $\bf{B}^\T{B}$.
- The non-zero singular values of $\bf{B}$ (found on the diagonal entries of $\bf{\Sigma}$) are the square roots of the non-zero eigenvalues of both $\bf{B}^\T\bf{B}$ and $\bf{B}^\T \bf{B}$.
with SVD we can write \bf{B} as \[\bf{B}=\bf{U\Sigma{{V}^{\T}}}\] where are \bf{U} and \bf{V} again unitary matrices and $\bf{\Sigma}$ stands for diagonal matrix of singular values.
Again we can solve either the system or compute pseudo inverse as
\[ \bf{B}^{-1} = \left( \bf{U\Sigma V}^\T\right)^{-1} = \bf{V}\bf{\Sigma^{-1}U}^\T \] where $\bf{\Sigma}^{-1}$ is trivial, just replace every non-zero diagonal entry by its reciprocal and transpose the resulting matrix. The stability gain is exactly here, one can now set threshold below which the singular value is considered as 0, basically truncate all singular values below some value and thus stabilize the inverse.
SVD decomposition complexity \[ 2mn^2+2n^3 = O(n^3) \]
Pros: stable cons: high complexity
End notes
- ↑ Note that our definition is a bit unusual, usually weights are not squared with the values. However, we do this to avoid computing square roots when doing MLS. If you are used to the usual definition, consider the weight to be $\omega^2$.