Difference between revisions of "Weighted Least Squares (WLS)"
| Line 10: | Line 10: | ||
\[{r^2} = \sum\limits_j^n {W\left( {{{\bf{p}}_j}} \right){{\left( {u({{\bf{p}}_j}) - \hat u({{\bf{p}}_j})} \right)}^2}} = {\left( {{\bf{B\alpha }} - {\bf{u}}} \right)^{\rm{T}}}{\bf{W}}\left( {{\bf{B\alpha }} - {\bf{u}}} \right)\] | \[{r^2} = \sum\limits_j^n {W\left( {{{\bf{p}}_j}} \right){{\left( {u({{\bf{p}}_j}) - \hat u({{\bf{p}}_j})} \right)}^2}} = {\left( {{\bf{B\alpha }} - {\bf{u}}} \right)^{\rm{T}}}{\bf{W}}\left( {{\bf{B\alpha }} - {\bf{u}}} \right)\] | ||
Where $\bf{B}$ is non-square matrix of dimension $m \times n$ and $\bf{W}$ diagonal matrix of weights. | Where $\bf{B}$ is non-square matrix of dimension $m \times n$ and $\bf{W}$ diagonal matrix of weights. | ||
| + | The least squares problem can be solved with three approaches | ||
| + | |||
| + | * Normal equation (fastest – less accurate) – using Cholesky decomposition | ||
| + | * QR decomposition (rank(B)=m – number of basis functions) | ||
| + | * SVD decomposition (more expensive – more reliable) | ||
Revision as of 17:26, 20 October 2016
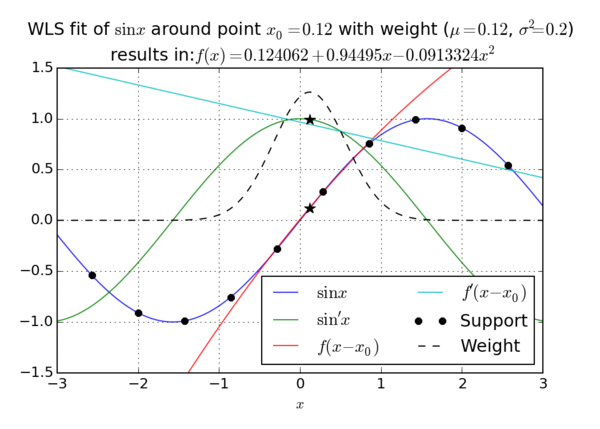
One of the most important building blocks of the meshless methods is the Moving Least Squares approximation, which is implemented in the EngineMLS class.
In general, approximation function can be written as \[\hat u({\bf{p}}) = \sum\limits_i^m {{\alpha _i}{b_i}({\bf{p}})} = {{\bf{b}}^{\rm{T}}}{\bf{\alpha }}\] where $\hat u,\,{B_i}\,and\,{\alpha _i}$ stand for approx. function, coefficients and basis function, respectively. We minimize the sum of residuum squares, i.e., the sum of squares of difference between the approx. function and target function, in addition we can also add weight function that controls the significance of nodes, i.e., \[{r^2} = \sum\limits_j^n {W\left( {{{\bf{p}}_j}} \right){{\left( {u({{\bf{p}}_j}) - \hat u({{\bf{p}}_j})} \right)}^2}} = {\left( {{\bf{B\alpha }} - {\bf{u}}} \right)^{\rm{T}}}{\bf{W}}\left( {{\bf{B\alpha }} - {\bf{u}}} \right)\] Where $\bf{B}$ is non-square matrix of dimension $m \times n$ and $\bf{W}$ diagonal matrix of weights. The least squares problem can be solved with three approaches
- Normal equation (fastest – less accurate) – using Cholesky decomposition
- QR decomposition (rank(B)=m – number of basis functions)
- SVD decomposition (more expensive – more reliable)