Revision as of 12:55, 6 July 2017

One of the most important building blocks of the meshless methods is the Moving Least Squares (MLS) approximation , which is implemented in the EngineMLS class. Check EngineMLS unit tests for examples.

Notation Cheat sheet

\begin{align*} m \in \N & \dots \text{number of basis functions} \\ n \geq m \in \N & \dots \text{number of points in support domain} \\ k \in \mathbb{N} & \dots \text{dimensionality of vector space} \\ \vec s_j \in \R^k & \dots \text{point in support domain } \quad j=1,\dots,n \\ u_j \in \R & \dots \text{value of function to approximate in }\vec{s}_j \quad j=1,\dots,n \\ \vec p \in \R^k & \dots \text{center point of approximation} \\ b_i\colon \R^k \to \R & \dots \text{basis functions } \quad i=1,\dots,m \\ B_{j, i} \in \R & \dots \text{value of basis functions in support points } b_i(s_j-p) \quad j=1,\dots,n, \quad i=1,\dots,m\\ \omega \colon \R^k \to \R & \dots \text{weight function} \\ w_j \in \R & \dots \text{weights } \omega(\vec{s}_j-\vec{p}) \quad j=1,\dots,n \\ \alpha_i \in \R & \dots \text{expansion coefficients around point } \vec{p} \quad i=1,\dots,m \\ \hat u\colon \R^k \to \R & \dots \text{approximation function (best fit)} \\ \chi_j \in \R & \dots \text{shape coefficient for point }\vec{p} \quad j=1,\dots,n \\ \end{align*}

We will also use \(\b{s}, \b{u}, \b{b}, \b{\alpha}, \b{\chi} \) to annotate a column of corresponding values, $W$ as a $n\times n$ diagonal matrix filled with $w_j$ on the diagonal and $B$ as a $n\times m$ matrix filled with $B_{j, i}$.

Definition of local approximation

Figure 1: Example of 1D WLS approximation

Our wish is to approximate an unknown function $u\colon \R^k \to \R$ while knowing $n$ values $u(\vec{s}_j) := u_j$. The vector of known values will be denoted by $\b{u}$ and the vector of coordinates where those values were achieved by $\b{s}$. Note that $\b{s}$ is not a vector in the usual sense since its components $\vec{s}_j$ are elements of $\R^k$, but we will call it vector anyway. The values of $\b{s}$ are called nodes or support nodes or support. The known values $\b{u}$ are also called support values.

In general, an approximation function around point $\vec{p}\in\R^k$ can be written as \[\hat{u} (\vec{x}) = \sum_{i=1}^m \alpha_i b_i(\vec{x}) = \b{b}(\vec{x})^\T \b{\alpha} \] where $\b{b} = (b_i)_{i=1}^m$ is a set of basis functions, $b_i\colon \R^k \to\R$, and $\b{\alpha} = (\alpha_i)_{i=1}^m$ are the unknown coefficients.

In MLS the goal is to minimize the error of approximation in given values, $\b{e} = \hat u(\b{s}) - \b{u}$ between the approximation function and target function in the known points $\b{x}$. The error can also be written as $B\b{\alpha} - \b{u}$, where $B$ is rectangular matrix of dimensions $n \times m$ with rows containing basis function evaluated in points $\vec{s}_j$. \[ B = \begin{bmatrix} b_1(\vec{s}_1) & \ldots & b_m(\vec{s}_1) \\ \vdots & \ddots & \vdots \\ b_1(\vec{s}_n) & \ldots & b_m(\vec{s}_n) \end{bmatrix} = [b_i(\vec{s}_j)]_{j=1,i=1}^{n,m} = [\b{b}(\vec{s}_j)^\T]_{j=1}^n. \]

We can choose to minimize any norm of the error vector $e$ and usually choose to minimize the $2$-norm or square norm \[ \|\b{e}\| = \|\b{e}\|_2 = \sqrt{\sum_{j=1}^n e_j^2}. \] Commonly, we also choose to minimize a weighted norm ^[1] instead \[ \|\b{e}\|_{2,w} = \|\b{e}\|_w = \sqrt{\sum_{j=1}^n (w_j e_j)^2}. \] The weights $w_i$ are assumed to be non negative and are assembled in a vector $\b{w}$ or a matrix $W = \operatorname{diag}(\b{w})$ and usually obtained from a weight function. A weight function is a function $\omega\colon \R^k \to[0,\infty)$. We calculate $w_j$ as $w_i := \omega(\vec{p}-\vec{s}_j)$, so good choices for $\omega$ are function which have higher values close to $0$ (making closer nodes more important), like the normal distribution. If we choose $\omega \equiv 1$, we get the unweighted version.

A choice of minimizing the square norm gave this method its name - Least Squares approximation. If we use the weighted version, we get the Weighted Least Squares or WLS. In the most general case we wish to minimize \[ \|\b{e}\|_{2,w}^2 = \b{e}^\T W^2 \b{e} = (B\b{\alpha} - \b{u})^\T W^2(B\b{\alpha} - \b{u}) = \sum_j^n w_j^2 (\hat{u}(\vec{s}_j) - u_j)^2 \]

The problem of finding the coefficients $\b{\alpha}$ that minimize the error $\b{e}$ can be solved with at least three approaches:

• Normal equations (fastest, less accurate) - using Cholesky decomposition of $B$ (requires full rank and $m \leq n$)
• QR decomposition of $B$ (requires full rank and $m \leq n$, more precise)
• SVD decomposition of $B$ (more expensive, even more reliable, no rank demand)

In our Meshless Machine MLS engine we use SVD with regularization described below.

Computing approximation coefficients

Normal equations

We seek the minimum of \[ \|\b{e}\|_2^2 = (B\b{\alpha} - \b{u})^\T(B\b{\alpha} - \b{u}) \] By seeking the zero gradient in terms of coefficients $\alpha_i$ \[\frac{\partial}{\partial \alpha_i} (B\b{\alpha} - \b{u})^\T(B\b{\alpha} - \b{u}) = 0\] resulting in \[ B^\T B\b{\alpha} = B^\T \b{u}. \] The coefficient matrix $B^\T B$ is symmetric and positive definite. However, solving above problem directly is poorly behaved with respect to round-off errors since the condition number $\kappa(B^\T B)$ is the square of $\kappa(B)$.

In case of WLS the equations become \[ (WB)^\T WB \b{\alpha} = WB^\T \b{u}. \]

Complexity of Cholesky decomposition is $\frac{n^3}{3}$ and complexity of matrix multiplication $nm^2$. To preform the Cholesky decomposition the rank of $WB$ must be full.

Pros:

• simple to implement
• low computational complexity

Cons:

• numerically unstable
• full rank requirement

$QR$ Decomposition

\[{\bf{B}} = {\bf{QR}} = \left[ {{{\bf{Q}}_1},{{\bf{Q}}_2}} \right]\left[ {\begin{array}{*{20}{c}} {{{\bf{R}}_1}}\\ 0 \end{array}} \right]\] \[{\bf{B}} = {{\bf{Q}}_1}{{\bf{R}}_1}\] $\bf{Q}$ is unitary matrix ($\bf{Q}^{-1}=\bf{Q}^T$). Useful property of a unitary matrices is that multiplying with them does not alter the (Euclidean) norm of a vector, i.e., \[\left\| {{\bf{Qx}}} \right\|{\bf{ = }}\left\| {\bf{x}} \right\|\] And $\bf{R}$ is upper diagonal matrix \[{\bf{R = (}}{{\bf{R}}_{\bf{1}}}{\bf{,}}0{\bf{)}}\] therefore we can say \[\begin{array}{l} \left\| {{\bf{B\alpha }} - {\bf{u}}} \right\| = \left\| {{{\bf{Q}}^{\rm{T}}}\left( {{\bf{B\alpha }} - {\bf{u}}} \right)} \right\| = \left\| {{{\bf{Q}}^{\rm{T}}}{\bf{B\alpha }} - {{\bf{Q}}^{\rm{T}}}{\bf{u}}} \right\|\\ = \left\| {{{\bf{Q}}^{\rm{T}}}\left( {{\bf{QR}}} \right){\bf{\alpha }} - {{\bf{Q}}^{\rm{T}}}{\bf{u}}} \right\| = \left\| {\left( {{{\bf{R}}_1},0} \right){\bf{\alpha }} - {{\left( {{{\bf{Q}}_1},{{\bf{Q}}_{\bf{2}}}} \right)}^{\rm{T}}}{\bf{u}}} \right\|\\ = \left\| {{{\bf{R}}_{\bf{1}}}{\bf{\alpha }} - {{\bf{Q}}_{\bf{1}}}{\bf{u}}} \right\| + \left\| {{\bf{Q}}_2^{\rm{T}}{\bf{u}}} \right\| \end{array}\] Of the two terms on the right we have no control over the second, and we can render the first one zero by solving \[{{\bf{R}}_{\bf{1}}}{\bf{\alpha }} = {\bf{Q}}_{_{\bf{1}}}^{\rm{T}}{\bf{u}}\] Which results in a minimum. We could also compute it with pseudo inverse \[\mathbf{\alpha }={{\mathbf{B}}^{-1}}\mathbf{u}\] Where pseudo inverse is simply \[{{\mathbf{B}}^{-1}}=\mathbf{R}_{\text{1}}^{\text{-1}}{{\mathbf{Q}}^{\text{T}}}\] (once again, $R$ is upper diagonal matrix, and $Q$ is unitary matrix). And for weighted case \[\mathbf{\alpha }={{\left( {{\mathbf{W}}^{0.5}}\mathbf{B} \right)}^{-1}}\left( {{\mathbf{W}}^{0.5}}\mathbf{u} \right)\]

Complexity of $QR$ decomposition \[\frac{2}{3}m{{n}^{2}}+{{n}^{2}}+\frac{1}{3}n-2=O({{n}^{3}})\]

Pros: better stability in comparison with normal equations cons: higher complexity

SVD decomposition

In linear algebra, the singular value decomposition (SVD) is a factorization of a real or complex matrix. It has many useful applications in signal processing and statistics.

Formally, the singular value decomposition of an $m \times n$ real or complex matrix $\bf{B}$ is a factorization of the form $\bf{B}= \bf{U\Sigma V^\T}$, where $\bf{U}$ is an $m \times m$ real or complex unitary matrix, $\bf{\Sigma}$ is an $m \times n$ rectangular diagonal matrix with non-negative real numbers on the diagonal, and $\bf{V}^\T$ is an $n \times n$ real or complex unitary matrix. The diagonal entries $\Sigma_{ii}$ are known as the singular values of $\bf{B}$. The $m$ columns of $\bf{U}$ and the $n$ columns of $\bf{V}$ are called the left-singular vectors and right-singular vectors of $\bf{B}$, respectively.

The singular value decomposition and the eigen decomposition are closely related. Namely:

• The left-singular vectors of $\bf{B}$ are eigen vectors of $\bf{BB}^\T$.
• The right-singular vectors of $\bf{B}$ are eigen vectors of $\bf{B}^\T{B}$.
• The non-zero singular values of $\bf{B}$ (found on the diagonal entries of $\bf{\Sigma}$) are the square roots of the non-zero eigenvalues of both $\bf{B}^\T\bf{B}$ and $\bf{B}^\T \bf{B}$.

with SVD we can write $\bf{B}$ as \[\bf{B}=\bf{U\Sigma{{V}^{\T}}}\] where are $\bf{U}$ and $\bf{V}$ again unitary matrices and $\bf{\Sigma}$ stands for diagonal matrix of singular values.

Again we can solve either the system or compute pseudo inverse as

\[ \bf{B}^{-1} = \left( \bf{U\Sigma V}^\T\right)^{-1} = \bf{V}\bf{\Sigma^{-1}U}^\T \] where $\bf{\Sigma}^{-1}$ is trivial, just replace every non-zero diagonal entry by its reciprocal and transpose the resulting matrix. The stability gain is exactly here, one can now set threshold below which the singular value is considered as $0$, basically truncate all singular values below some value and thus stabilize the inverse.

SVD decomposition complexity \[ 2mn^2+2n^3 = O(n^3) \]

Pros: stable cons: high complexity

Method used in MLSM is SVD with regularization.

Weighted Least Squares

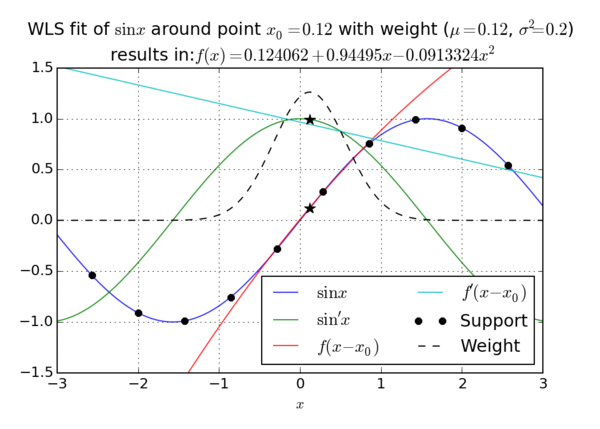
Weighted least squares approximation is the simplest version of the procedure described above. Given support $\b{s}$, values $\b{u}$ and an anchor point $\vec{p}$, we calculate the coefficients $\b{\alpha}$ using one of the above methods. Then, to approximate a function in the neighbourhood of $\vec p$ we use the formula \[ \hat{u}(\vec x) = \b{b}(\vec x)^\T \b{\alpha} = \sum_{i=1}^m \alpha_i b_i(\vec x). \]

To approximate the derivative $\frac{\partial u}{\partial x_i}$, or any linear partial differential operator $\mathcal L$ on $u$, we simply take the same linear combination of transformed basis functions $\mathcal L b_i$. We have considered coefficients $\alpha_i$ to be constant and applied the linearity. \[ \widehat{\mathcal L u}(\vec x) = \sum_{i=1}^m \alpha_i (\mathcal L b_i)(\vec x). \]

WLS at fixed point with fixed support and unknown function values :: Shape functions

Suppose now we are given support $\b{s}$ and a point $\b{p}$ and want to construct the function approximation from values $\b{u}$. We proceed as usual, solving the overdetermined system $WB \b{\alpha} = W\b{u}$ for coefficients $\b{\alpha}$ using the pseudoinverse \[ \b{\alpha} = (WB)^+W\b{u}, \] where $A^+$ denotes the Moore-Penrose pseudoinverse that can be calculated using SVD.

Writing down the approximation function $\hat{u}$ we get \[ \hat u (\vec{p}) = \b{b}(\vec{p})^\T \b{\alpha} = \b{b}(\vec{p})^\T (WB)^+W\b{u} = \b{\chi}(\vec{p}) \b{u}. \]

We have defined $\b{\chi}$ to be \[ \b{\chi}(\vec{p}) = \b{b}(\vec{p})^\T (WB)^+W. \] Vector $\b{\chi}$ is a row vector, also called a shape function. The name comes from being able to take all the information about shape of the domain and choice of approximation and store it in a single row vector, being able to approximate a function value from given support values $\b{u}$ with a single dot product. For any values $\b{u}$, value $\b{\chi}(p) \b{u}$ gives us the approximation $\hat{u}(\vec{p})$ of $u$ in point $\vec{p}$. Mathematically speaking, $\b{\chi}(\vec{p})$ is a functional, $\b{\chi}(\vec{p})\colon \R^n \to \R$, mapping $n$-tuples of known function values to their approximations in point $\vec{p}$.

The same approach works for any linear operator $\mathcal L$ applied to $u$, just replace every $b_i$ in definition of $\b{\chi}$ with $\mathcal Lb_i$. For example, take a $1$-dimensional case for approximation of derivatives with weight equal to $1$ and $n=m=3$, with equally spaced support values at distances $h$. We wish to approximate $u''$ in the middle support point, just by making a weighted sum of the values, something like the finite difference \[ u'' \approx \frac{u_1 - 2u_2 + u_3}{h^2}. \] This is exactly the same formula as we would have come to by computing $\b{\chi}$, except that our approach is a lot more general. But one should think about $\b{\chi}$ as one would about the finite difference scheme, it is a rule, telling us how to compute the derivative. \[ u''(s_2) \approx \underbrace{\begin{bmatrix} \frac{1}{h^2} & \frac{-2}{h^2} & \frac{1}{h^2} \end{bmatrix}}_{\b{\chi}} \begin{bmatrix}u_1 \\ u_2 \\ u_3 \end{bmatrix} \]

The fact that $\b{\chi}$ is independent of the function values $\b{u}$ but depend only on domain geometry means that we can just compute the shape functions $\b{\chi}$ for points of interest and then approximate any linear operator of any function, given its values, very fast, using only a single dot product.

Numerical calculation of the shape functions

The formula \[ \b{\chi}(\vec{p}) = \b{b}(\vec{p})^\T (WB)^+W \] can be evaluated directly numerically, but this is not the best way. A cheaper and more numerically stable way is to convert inverting the matrix to solving a system of equations.

Invertible $B$ case: Iz $B$ is invertible, then $\b{\chi}(\vec{p}) = \b{b}(\vec{p})^\T B^{-1}$, and transposing the eqaution and multiplying from the right by $B$, $\b{\chi}$ can be thought as a solution of a system $B^\T\chi(\vec{p})^\T = \b{b}(\vec{p})$, which can be solved using LU decomposition for example.

General case: For a system written as $Ax = b$, where a is a $n\times m$ matrix, $x$ is a vector of length $m$ and $b$ a vector of length $m$, a generalized solution $x$ is defined as such an $x$ that minimizes $\|A x - b\|_2^2$. If more such $x$ attain the minimal value, $x$ with the minimal $\|x\|$ is chosen. Note that this generalizes the solution a general sistem ($A$ is invertible) and overdetermined system ($n > m$ and $A$ has full rank). Such an $x$ can be computed using the pseudoinverse $x = A^{+} b$.

In our case, let us denote a part of the solution containing the pseudoinverse by $\tilde{\b{\chi}}$. \[ \b{\chi}(\vec{p}) = \underbrace{\b{b}(\vec{p})^\T (WB)^+}_{\tilde{\b{\chi}}} W \] We have an expression $\tilde{\b{\chi}} = \b{b}(\vec{p})^\T (WB)^+$ which after transposition takes the form $\tilde{\b{\chi}}^\T = ((WB)^\T)^+\b{b}(\vec{p})$, the same as $x = A^+b$ above. Therefore, $\tilde{\b{\chi}}^\T$ is the solution of an (indeterminate) system $(WB)^\T \tilde{\b{\chi}}^\T = \b{b}(\vec{p})$. After solving that, we can get the shape function $\b\chi(\vec{p}) = \tilde{\b{\chi}} W$ by multiplying by matrix $W$. The system before can be solved using any decomposition of matrix $(WB)^\T = B^\T W$ necessary, mosr generally the SVD decompostion, but depending on our knowledge of the problem, we can use Cholesky ($B^\T W$ is positive definite), $LDL^\T$ if it is symmetric, $LU$ for a general square matrix, $QR$ for full rank overdetermined system and SVD for a general system. Is more shapes need to be calculated using the same matrix $B^\T W$ and only different right hand sides, it can be done efficiently by storing the decomposition of $B^\T W$.

MLS

Figure 2: Comparison of WLS and MLS approximation

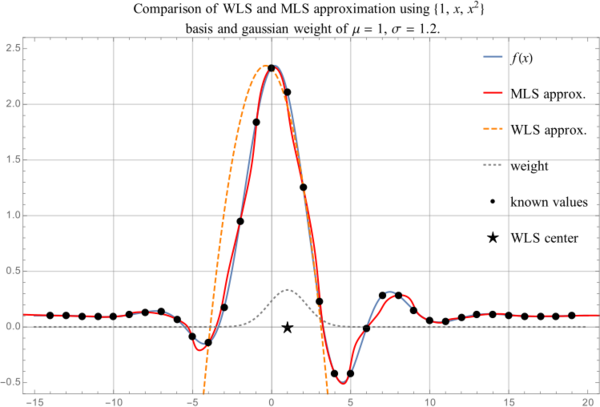
When using WLS the approximation gets worse as we move away from the central point $\vec{p}$. This is partially due to not being in the center of the support any more and partially due to weight being distributed in such a way to assign more importance to nodes closer to $\vec{p}$.

We can battle this problem in two ways: when we wish to approximate in a new point that is sufficiently far away from $\vec{p}$ we can compute new support, recompute the new coefficients $\b{\alpha}$ and approximate again. This is very costly and we would like to avoid that. A partial fix is to keep support the same, but only recompute the weight vector $\b{w}$, that will now assign weight values to nodes close to the new point. We still need to recompute the coefficients $\b{\alpha}$, however we avoid the cost of setting up new support and function values and recomputing $B$. This approach is called Moving Least Squares due to recomputing the weighted least squares problem whenever we move the point of approximation.

Note that if out weight is constant or if $n = m$, when approximation reduces to interpolation, the weights do not play any role and this method is redundant. In fact, its benefits arise when supports are rather large.

See Figure 2 for comparison between MLS and WLS approximations. MLS approximation remains close to actual function while still inside the support domain, while WLS approximation becomes bad when we come out of the reach of the weight function.

End notes

1. ↑ Note that our definition is a bit unusual, usually weights are not squared with the values. However, we do this to avoid computing square roots when doing MLS. If you are used to the usual definition, consider the weight to be $\omega^2$.