Difference between revisions of "Weighted Least Squares (WLS)"

From Medusa: Coordinate Free Mehless Method implementation
Jump to: navigation, search
(→‎Shape functions)
m (Typos)
 
(149 intermediate revisions by 6 users not shown)
Line 1: Line 1:
−
One of the most important building blocks of the meshless methods is the Moving Least Squares approximation, which is implemented in the [http://www-e6.ijs.si/ParallelAndDistributedSystems/MeshlessMachine/technical_docs/html/classEngineMLS.html EngineMLS class]. Check EngineMLS unit tests for examples https://gitlab.com/e62Lab/e62numcodes/blob/master/test/mls_test.cpp
+
One of the most important building blocks of the meshless methods is the Weighted/Moving Least Squares (WLS/MLS) approximation , which is implemented in the <code>WLS</code> class.
 +
It is also often called GFDM (generalized finite differences method).
  
−
<figure id="fig:square_heat">
+
= Notation cheat sheet =
−
[[File:image_1avhdsfej1b9cao01029m1e13o69.png|600px|thumb|upright=2|alt=1D MLS example|<caption>Example of 1D MLS approximation </caption>]]
+
\begin{align*}
 +
  m \in \N                  & \dots \text{number of basis functions} \\
 +
  n \geq m \in \N          & \dots \text{number of points in support domain} \\
 +
  k \in \mathbb{N}          & \dots \text{dimensionality of vector space} \\
 +
  \vec s_j \in \R^k        & \dots \text{point in support domain } \quad j=1,\dots,n \\
 +
  u_j \in \R                & \dots \text{value of function to approximate in }\vec{s}_j \quad j=1,\dots,n \\
 +
  \vec p \in \R^k          & \dots \text{center point of approximation} \\
 +
  b_i\colon \R^k \to \R    & \dots \text{basis functions } \quad i=1,\dots,m \\
 +
  B_{j, i} \in \R          & \dots \text{value of basis functions in support points } b_i(\vec{s}_j) \quad j=1,\dots,n, \quad i=1,\dots,m\\
 +
  \omega \colon \R^k \to \R & \dots \text{weight function} \\
 +
  w_j \in \R                & \dots \text{weights } \omega(\vec{s}_j-\vec{p})  \quad j=1,\dots,n \\
 +
  \alpha_i \in \R          & \dots \text{expansion coefficients around point } \vec{p} \quad i=1,\dots,m \\
 +
  \hat u\colon \R^k \to \R  & \dots \text{approximation function (best fit)} \\
 +
  \chi_j \in \R          & \dots \text{shape coefficient for point }\vec{p} \quad j=1,\dots,n \\
 +
\end{align*}
 +
 
 +
We will also use \(\b{s}, \b{u}, \b{b}, \b{\alpha}, \b{\chi} \) to denote a column of corresponding values,
 +
$W$ as a $n\times n$ diagonal matrix filled with $w_j$ on the diagonal and $B$ as a $n\times m$ matrix filled with $B_{j, i} = b_i(\vec s_j)$.
 +
 
 +
= Definition of local approximation =
 +
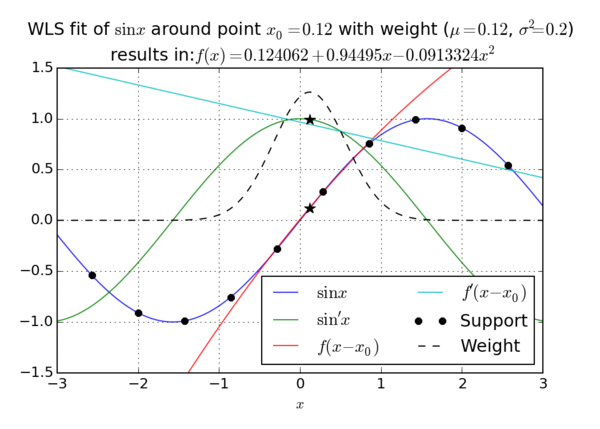
<figure id="fig:1DWLS">
 +
[[File:image_1avhdsfej1b9cao01029m1e13o69.png|600px|thumb|upright=2|alt=1D MLS example|<caption>Example of 1D WLS approximation </caption>]]
 
</figure>
 
</figure>
−
== Basics ==
+
Our wish is to approximate an unknown function $u\colon \R^k \to \R$ while knowing $n$ values $u(\vec{s}_j) := u_j$.
−
In general, approximation function can be written as
+
The vector of known values will be denoted by $\b{u}$ and the vector of coordinates where those values were achieved by $\b{s}$.
−
\[\hat u({\bf{p}}) = \sum\limits_i^m {{\alpha _i}{b_i}({\bf{p}})}  = {{\bf{b}}^{\rm{T}}}{\bf{\alpha }}\]
+
Note that $\b{s}$ is not a vector in the usual sense since its components $\vec{s}_j$ are elements of $\R^k$, but we will call it vector anyway.
−
where $\hat u,\,{B_i}\,and\,{\alpha _i}$ stand for approx. function, coefficients and basis function, respectively. We minimize the sum of residuum squares, i.e., the sum of squares of difference between the approx. function and target function, in addition we can also add weight function that controls the significance of nodes, i.e.,
+
The values of $\b{s}$ are called ''nodes'' or ''support nodes'' or ''support''. The known values $\b{u}$ are also called ''support values''.
−
\[{r^2} = \sum\limits_j^n {W\left( {{{\bf{p}}_j}} \right){{\left( {u({{\bf{p}}_j}) - \hat u({{\bf{p}}_j})} \right)}^2}}  = {\left( {{\bf{B\alpha }} - {\bf{u}}} \right)^{\rm{T}}}{\bf{W}}\left( {{\bf{B\alpha }} - {\bf{u}}} \right)\]
 
−
Where $\bf{B}$ is non-square matrix of dimension $m \times n$ and $\bf{W}$ diagonal matrix of weights.
 
−
The least squares problem can be solved with three approaches
 
  
−
* Normal equation (fastest – less accurate) – using Cholesky decomposition
+
In general, an approximation function around point $\vec{p}\in\R^k$ can be
−
* QR decomposition of $\bf{B}$ ($rank(\bf{B})=m$ – number of basis functions)
+
written as \[\hat{u} (\vec{x}) = \sum_{i=1}^m \alpha_i b_i(\vec{x}) = \b{b}(\vec{x})^\T \b{\alpha} \]
−
* SVD decomposition of $\bf{B}$ (more expensive – more reliable, no rank demand)
+
where $\b{b} = (b_i)_{i=1}^m$ is a set of ''basis functions'', $b_i\colon \R^k \to\R$, and $\b{\alpha} = (\alpha_i)_{i=1}^m$ are the unknown coefficients.
  
−
In MM we use SVD.
+
In MLS the goal is to minimize the error of approximation in given values, $\b{e} = \hat u(\b{s}) - \b{u}$
 +
between the approximation function and target function in the known points $\b{x}$. The error can also be written as $B\b{\alpha} - \b{u}$,
 +
where $B$ is rectangular matrix of dimensions $n \times m$ with rows containing basis function evaluated in points $\vec{s}_j$.
 +
\[ B =
 +
\begin{bmatrix}
 +
b_1(\vec{s}_1) & \ldots & b_m(\vec{s}_1) \\
 +
\vdots & \ddots & \vdots \\
 +
b_1(\vec{s}_n) & \ldots & b_m(\vec{s}_n)
 +
\end{bmatrix} =
 +
[b_i(\vec{s}_j)]_{j=1,i=1}^{n,m} = [\b{b}(\vec{s}_j)^\T]_{j=1}^n. \]
  
−
== Normal equations ==
+
We can choose to minimize any norm of the error vector $e$
−
We seek the minimum of
+
and usually choose to minimize the $2$-norm or square norm \[ \|\b{e}\| = \|\b{e}\|_2 = \sqrt{\sum_{j=1}^n e_j^2}. \]
−
\[{\bf{r}} = {\bf{u}} - {\bf{B\alpha }}\], \[{r^2} = {\left( {{\bf{u}} - {\bf{B\alpha }}} \right)^{\rm{T}}}\left( {{\bf{u}} - {\bf{B\alpha }}} \right)\]
+
Commonly, we also choose to minimize a weighted norm
−
By seeking the zero gradient in terms of coefficient
+
<ref>Note that our definition is a bit unusual, usually weights are not
−
\[\frac{\partial }{{\partial {\alpha _i}}}\left( {{{\left( {{\bf{u}} - {\bf{B\alpha }}} \right)}^{\rm{T}}}\left( {{\bf{u}} - {\bf{B\alpha }}} \right)} \right) = 0\]
+
squared with the values. However, we do this to avoid computing square
−
resulting in
+
roots when doing MLS. If you are used to the usual definition,
−
\[{\bf{B}}{{\bf{B}}^{\rm{T}}}{\bf{\alpha }} = {{\bf{B}}^{\rm{T}}}{\bf{u}}\]
+
consider the weight to be $\omega^2$.</ref>
−
The coefficient matrix $\bf{B}^T\bf{B}$ is symmetric and positive definite. However, solving above problem directly is
+
instead \[ \|\b{e}\|_{2,w} = \|\b{e}\|_w = \sqrt{\sum_{j=1}^n (w_j e_j)^2}. \]
−
poorly behaved with respect to round-off effects since the condition number of $\bf{B}^T\bf{B}$is the square
+
The ''weights'' $w_i$ are assumed to be non negative and are assembled in a vector $\b{w}$ or a matrix $W = \operatorname{diag}(\b{w})$ and usually obtained from a weight function.
−
of that of $\bf{B}$. Or in case of weighted LS
+
A ''weight function'' is a function $\omega\colon \R^k \to[0,\infty)$. We calculate $w_j$ as $w_i := \omega(\vec{p}-\vec{s}_j)$, so
−
\[{\bf{WB}}{{\bf{B}}^{\rm{T}}}{\bf{\alpha }} = {\bf{W}}{{\bf{B}}^{\rm{T}}}{\bf{u}}\]
+
good choices for $\omega$ are function which have higher values close to $0$ (making closer nodes more important), like the normal distribution.
 +
If we choose $\omega \equiv 1$, we get the unweighted version.
  
−
Complexity of Chol: $\frac{{{n}^{3}}}{3}$ complexity of matrix multiplication $n{{m}^{2}}$
+
A choice of minimizing the square norm gave this method its name - Least Squares approximation. If we use the weighted version, we get the Weighted Least Squares or WLS.
 +
In the most general case we wish to minimize
 +
\[ \|\b{e}\|_{2,w}^2 = \b{e}^\T W^2 \b{e} = (B\b{\alpha} - \b{u})^\T W^2(B\b{\alpha} - \b{u}) = \sum_j^n w_j^2 (\hat{u}(\vec{s}_j) - u_j)^2 \]
  
−
== QR Decomposition ==
 
−
\[{\bf{B}} = {\bf{QR}} = \left[ {{{\bf{Q}}_1},{{\bf{Q}}_2}} \right]\left[ {\begin{array}{*{20}{c}}
 
−
{{{\bf{R}}_1}}\\
 
−
0
 
−
\end{array}} \right]\]
 
−
\[{\bf{B}} = {{\bf{Q}}_1}{{\bf{R}}_1}\]
 
−
$\bf{Q}$ is unitary matrix ($\bf{Q}^{-1}=\bf{Q}^T$). Useful property of a unitary matrices is that multiplying with them does not alter the (Euclidean) norm of a vector, i.e.,
 
−
\[\left\| {{\bf{Qx}}} \right\|{\bf{ = }}\left\| {\bf{x}} \right\|\]
 
−
And $\bf{R}$ is upper diagonal matrix
 
−
\[{\bf{R = (}}{{\bf{R}}_{\bf{1}}}{\bf{,}}0{\bf{)}}\]
 
−
therefore we can say
 
−
\[\begin{array}{l}
 
−
\left\| {{\bf{B\alpha }} - {\bf{u}}} \right\| = \left\| {{{\bf{Q}}^{\rm{T}}}\left( {{\bf{B\alpha }} - {\bf{u}}} \right)} \right\| = \left\| {{{\bf{Q}}^{\rm{T}}}{\bf{B\alpha }} - {{\bf{Q}}^{\rm{T}}}{\bf{u}}} \right\|\\
 
−
= \left\| {{{\bf{Q}}^{\rm{T}}}\left( {{\bf{QR}}} \right){\bf{\alpha }} - {{\bf{Q}}^{\rm{T}}}{\bf{u}}} \right\| = \left\| {\left( {{{\bf{R}}_1},0} \right){\bf{\alpha }} - {{\left( {{{\bf{Q}}_1},{{\bf{Q}}_{\bf{2}}}} \right)}^{\rm{T}}}{\bf{u}}} \right\|\\
 
−
= \left\| {{{\bf{R}}_{\bf{1}}}{\bf{\alpha }} - {{\bf{Q}}_{\bf{1}}}{\bf{u}}} \right\| + \left\| {{\bf{Q}}_2^{\rm{T}}{\bf{u}}} \right\|
 
−
\end{array}\]
 
−
Of the two terms on the right we have no control over the second, and we can render the first one
 
−
zero by solving
 
−
\[{{\bf{R}}_{\bf{1}}}{\bf{\alpha }} = {\bf{Q}}_{_{\bf{1}}}^{\rm{T}}{\bf{u}}\]
 
−
Which results in a minimum. We could also compute it with pseudo inverse
 
−
\[\mathbf{\alpha }={{\mathbf{B}}^{-1}}\mathbf{u}\]
 
−
Where pseudo inverse is simply \[{{\mathbf{B}}^{-1}}=\mathbf{R}_{\text{1}}^{\text{-1}}{{\mathbf{Q}}^{\text{T}}}\] (once again, R is upper diagonal matrix, and Q is unitary matrix).
 
−
And for weighted case
 
−
\[\mathbf{\alpha }={{\left( {{\mathbf{W}}^{0.5}}\mathbf{B} \right)}^{-1}}\left( {{\mathbf{W}}^{0.5}}\mathbf{u} \right)\]
 
  
−
Complexity of QR decomposition \[\frac{2}{3}m{{n}^{2}}+{{n}^{2}}+\frac{1}{3}n-2=O({{n}^{3}})\]
+
The problem of finding the coefficients $\b{\alpha}$ that minimize the error $\b{e}$ numerically is described in [[Solving overdetermined systems]].
  
−
== SVD decomposition ==
+
Here, we simply write the solution $\b \alpha = (WB)^+ Wu = (B^\T W^2 B)^{-1} B^\T W^2 u$.
−
In linear algebra, the singular value decomposition (SVD) is a factorization of a real or complex matrix. It has many useful applications in signal processing and statistics.
 
  
−
Formally, the singular value decomposition of an m × n real or complex matrix $\bf{B}$ is a factorization of the form $\bf{B}= \bf{UΣV}*$, where $\bf{U}$ is an m × m real or complex unitary matrix, $\bf{Σ}$ is an m × n rectangular diagonal matrix with non-negative real numbers on the diagonal, and $\bf{V*}$  is an n × n real or complex unitary matrix. The diagonal entries Σ_{i,i} of are known as the singular values of $\bf{B}$. The m columns of $\bf{U}$ and the n columns of $\bf{V}$ are called the left-singular vectors and right-singular vectors of $\bf{B}$, respectively.
+
In our WLS engine we use SVD with regularization by default.
  
−
The singular value decomposition and the eigen decomposition are closely related. Namely:
+
= Weighted Least Squares =
−
* The left-singular vectors of $\bf{B}$ are eigen vectors of $\bf{B*B^*}$.
+
Weighted least squares approximation is the simplest version of the procedure described above. Given support $\b{s}$, values $\b{u}$
−
* The right-singular vectors of $\bf{B}$ are eigen vectors of $\bf{B*B}$.
+
and an anchor point $\vec{p}$, we calculate the coefficients $\b{\alpha}$ using one of the above methods.
−
* The non-zero singular values of $\bf{B}$ (found on the diagonal entries of $\bf{Σ}$) are the square roots of the non-zero eigenvalues of both $\bf{B*B}$ and $\bf{B*B^*}$.
+
Then, to approximate a function in the neighbourhood of $\vec p$ we use the formula
 +
\[
 +
\hat{u}(\vec x) = \b{b}(\vec x)^\T \b{\alpha} = \sum_{i=1}^m \alpha_i b_i(\vec x).
 +
\]
  
−
with SVD we can write B as
+
To approximate the derivative $\frac{\partial u}{\partial x_i}$, or any linear partial differential operator $\mathcal L$ on $u$, we
−
\[\mathbf{B}=\mathbf{U}\sum {{\mathbf{V}}^{\text{T}}}\]
+
simply take the same linear combination of transformed basis functions $\mathcal L b_i$. We have considered coefficients $\alpha_i$ to be
−
where are U and V again unitary matrices and \[\sum \] stands for diagonal matrix of singular values. 
+
constant and applied the linearity.
 +
\[
 +
\widehat{\mathcal L u}(\vec x) = \sum_{i=1}^m \alpha_i (\mathcal L b_i)(\vec x) = (\mathcal L \b b(\vec x))^\T \b \alpha.
 +
\]
 +
 
 +
= Moving Least Squares =
 +
 
 +
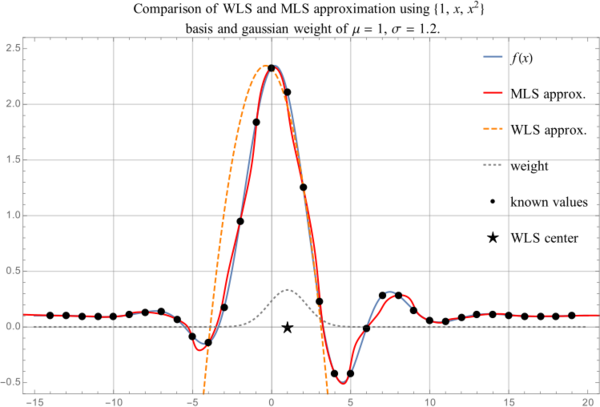
<figure id="fig:comparisonMLSandWLS">
 +
[[File:mlswls.svg|thumb|upright=2|<caption>Comparison of WLS and MLS approximation</caption>]]
 +
</figure>
  
−
Again we can solve either the system or compute pseudo inverse as
+
When using WLS the approximation gets worse as we move away from the central point $\vec{p}$.
−
\[{{\mathbf{B}}^{-1}}={{\left( \mathbf{U}\sum {{\mathbf{V}}^{\text{T}}} \right)}^{-1}}=\mathbf{V}{{\sum }^{-1}}{{\mathbf{U}}^{\text{T}}}\],
+
This is partially due to not being in the center of the support any more and partially due to weight
−
where $\bf{Σ}$^-1 is trivial, just replace every non-zero diagonal entry by its reciprocal and transpose the resulting matrix. The stability gain is exactly here, one can now set threshold below which the singular value is considered as 0, basically truncate all singular values below some value and thus stabilize the inverse.
+
being distributed in such a way to assign more importance to nodes closer to $\vec{p}$.
  
−
SVD decomposition complexity \[2m{{n}^{2}}~+\text{ }2{{n}^{3}}=O({{n}^{3}})\]
+
We can battle this problem in two ways: when we wish to approximate in a new point that is sufficiently far
 +
away from $\vec{p}$ we can compute new support, recompute the new coefficients $\b{\alpha}$ and approximate again.
 +
This is very costly and we would like to avoid that. A partial fix is to keep support the same, but only
 +
recompute the weight vector $\b{w}$, that will now assign weight values to nodes close to the new point.
 +
We still need to recompute the coefficients $\b{\alpha}$, however we avoid the cost of setting up new support
 +
and function values and recomputing $B$. This approach is called Moving Least Squares due to recomputing
 +
the weighted least squares problem whenever we move the point of approximation.
  
−
== Shape functions ==
+
Note that if our weight is constant or if $n = m$, when approximation reduces to interpolation, the weights do not play
 +
any role and this method is redundant. In fact, its benefits arise when supports are rather large.
  
 +
See <xr id="fig:comparisonMLSandWLS"/> for comparison between MLS and WLS approximations. MLS approximation remains close to
 +
the actual function while still inside the support domain, while WLS approximation becomes bad when
 +
we come out of the reach of the weight function.
  
−
\[\hat{u}(\mathbf{p})={{\mathbf{b}}^{\text{T}}}\mathbf{\alpha }\]
+
{{reflist}}
−
Express coefficients explicitly from (2.77)
 
−
\[\hat{u}(\mathbf{p})={{\mathbf{b}}^{\text{T}}}{{\mathbf{B}}^{-1}}\mathbf{u}=\mathbf{\Phi u}\]
 
−
where \[\mathbf{\Phi }\] stand for shape functions, and weighted variant
 
−
\[\hat{u}(\mathbf{p})={{\mathbf{b}}^{\text{T}}}{{\left( {{\mathbf{W}}^{0.5}}\mathbf{B} \right)}^{-1}}{{\mathbf{W}}^{0.5}}\mathbf{u}=\mathbf{\Phi u}\]
 

Latest revision as of 14:57, 16 June 2022

One of the most important building blocks of the meshless methods is the Weighted/Moving Least Squares (WLS/MLS) approximation , which is implemented in the WLS class. It is also often called GFDM (generalized finite differences method).

Notation cheat sheet

\begin{align*} m \in \N & \dots \text{number of basis functions} \\ n \geq m \in \N & \dots \text{number of points in support domain} \\ k \in \mathbb{N} & \dots \text{dimensionality of vector space} \\ \vec s_j \in \R^k & \dots \text{point in support domain } \quad j=1,\dots,n \\ u_j \in \R & \dots \text{value of function to approximate in }\vec{s}_j \quad j=1,\dots,n \\ \vec p \in \R^k & \dots \text{center point of approximation} \\ b_i\colon \R^k \to \R & \dots \text{basis functions } \quad i=1,\dots,m \\ B_{j, i} \in \R & \dots \text{value of basis functions in support points } b_i(\vec{s}_j) \quad j=1,\dots,n, \quad i=1,\dots,m\\ \omega \colon \R^k \to \R & \dots \text{weight function} \\ w_j \in \R & \dots \text{weights } \omega(\vec{s}_j-\vec{p}) \quad j=1,\dots,n \\ \alpha_i \in \R & \dots \text{expansion coefficients around point } \vec{p} \quad i=1,\dots,m \\ \hat u\colon \R^k \to \R & \dots \text{approximation function (best fit)} \\ \chi_j \in \R & \dots \text{shape coefficient for point }\vec{p} \quad j=1,\dots,n \\ \end{align*}

We will also use \(\b{s}, \b{u}, \b{b}, \b{\alpha}, \b{\chi} \) to denote a column of corresponding values, $W$ as a $n\times n$ diagonal matrix filled with $w_j$ on the diagonal and $B$ as a $n\times m$ matrix filled with $B_{j, i} = b_i(\vec s_j)$.

Definition of local approximation

1D MLS example
Figure 1: Example of 1D WLS approximation

Our wish is to approximate an unknown function $u\colon \R^k \to \R$ while knowing $n$ values $u(\vec{s}_j) := u_j$. The vector of known values will be denoted by $\b{u}$ and the vector of coordinates where those values were achieved by $\b{s}$. Note that $\b{s}$ is not a vector in the usual sense since its components $\vec{s}_j$ are elements of $\R^k$, but we will call it vector anyway. The values of $\b{s}$ are called nodes or support nodes or support. The known values $\b{u}$ are also called support values.

In general, an approximation function around point $\vec{p}\in\R^k$ can be written as \[\hat{u} (\vec{x}) = \sum_{i=1}^m \alpha_i b_i(\vec{x}) = \b{b}(\vec{x})^\T \b{\alpha} \] where $\b{b} = (b_i)_{i=1}^m$ is a set of basis functions, $b_i\colon \R^k \to\R$, and $\b{\alpha} = (\alpha_i)_{i=1}^m$ are the unknown coefficients.

In MLS the goal is to minimize the error of approximation in given values, $\b{e} = \hat u(\b{s}) - \b{u}$ between the approximation function and target function in the known points $\b{x}$. The error can also be written as $B\b{\alpha} - \b{u}$, where $B$ is rectangular matrix of dimensions $n \times m$ with rows containing basis function evaluated in points $\vec{s}_j$. \[ B = \begin{bmatrix} b_1(\vec{s}_1) & \ldots & b_m(\vec{s}_1) \\ \vdots & \ddots & \vdots \\ b_1(\vec{s}_n) & \ldots & b_m(\vec{s}_n) \end{bmatrix} = [b_i(\vec{s}_j)]_{j=1,i=1}^{n,m} = [\b{b}(\vec{s}_j)^\T]_{j=1}^n. \]

We can choose to minimize any norm of the error vector $e$ and usually choose to minimize the $2$-norm or square norm \[ \|\b{e}\| = \|\b{e}\|_2 = \sqrt{\sum_{j=1}^n e_j^2}. \] Commonly, we also choose to minimize a weighted norm [1] instead \[ \|\b{e}\|_{2,w} = \|\b{e}\|_w = \sqrt{\sum_{j=1}^n (w_j e_j)^2}. \] The weights $w_i$ are assumed to be non negative and are assembled in a vector $\b{w}$ or a matrix $W = \operatorname{diag}(\b{w})$ and usually obtained from a weight function. A weight function is a function $\omega\colon \R^k \to[0,\infty)$. We calculate $w_j$ as $w_i := \omega(\vec{p}-\vec{s}_j)$, so good choices for $\omega$ are function which have higher values close to $0$ (making closer nodes more important), like the normal distribution. If we choose $\omega \equiv 1$, we get the unweighted version.

A choice of minimizing the square norm gave this method its name - Least Squares approximation. If we use the weighted version, we get the Weighted Least Squares or WLS. In the most general case we wish to minimize \[ \|\b{e}\|_{2,w}^2 = \b{e}^\T W^2 \b{e} = (B\b{\alpha} - \b{u})^\T W^2(B\b{\alpha} - \b{u}) = \sum_j^n w_j^2 (\hat{u}(\vec{s}_j) - u_j)^2 \]


The problem of finding the coefficients $\b{\alpha}$ that minimize the error $\b{e}$ numerically is described in Solving overdetermined systems.

Here, we simply write the solution $\b \alpha = (WB)^+ Wu = (B^\T W^2 B)^{-1} B^\T W^2 u$.

In our WLS engine we use SVD with regularization by default.

Weighted Least Squares

Weighted least squares approximation is the simplest version of the procedure described above. Given support $\b{s}$, values $\b{u}$ and an anchor point $\vec{p}$, we calculate the coefficients $\b{\alpha}$ using one of the above methods. Then, to approximate a function in the neighbourhood of $\vec p$ we use the formula \[ \hat{u}(\vec x) = \b{b}(\vec x)^\T \b{\alpha} = \sum_{i=1}^m \alpha_i b_i(\vec x). \]

To approximate the derivative $\frac{\partial u}{\partial x_i}$, or any linear partial differential operator $\mathcal L$ on $u$, we simply take the same linear combination of transformed basis functions $\mathcal L b_i$. We have considered coefficients $\alpha_i$ to be constant and applied the linearity. \[ \widehat{\mathcal L u}(\vec x) = \sum_{i=1}^m \alpha_i (\mathcal L b_i)(\vec x) = (\mathcal L \b b(\vec x))^\T \b \alpha. \]

Moving Least Squares

Figure 2: Comparison of WLS and MLS approximation

When using WLS the approximation gets worse as we move away from the central point $\vec{p}$. This is partially due to not being in the center of the support any more and partially due to weight being distributed in such a way to assign more importance to nodes closer to $\vec{p}$.

We can battle this problem in two ways: when we wish to approximate in a new point that is sufficiently far away from $\vec{p}$ we can compute new support, recompute the new coefficients $\b{\alpha}$ and approximate again. This is very costly and we would like to avoid that. A partial fix is to keep support the same, but only recompute the weight vector $\b{w}$, that will now assign weight values to nodes close to the new point. We still need to recompute the coefficients $\b{\alpha}$, however we avoid the cost of setting up new support and function values and recomputing $B$. This approach is called Moving Least Squares due to recomputing the weighted least squares problem whenever we move the point of approximation.

Note that if our weight is constant or if $n = m$, when approximation reduces to interpolation, the weights do not play any role and this method is redundant. In fact, its benefits arise when supports are rather large.

See Figure 2 for comparison between MLS and WLS approximations. MLS approximation remains close to the actual function while still inside the support domain, while WLS approximation becomes bad when we come out of the reach of the weight function.

End notes

  1. ↑ Note that our definition is a bit unusual, usually weights are not squared with the values. However, we do this to avoid computing square roots when doing MLS. If you are used to the usual definition, consider the weight to be $\omega^2$.
Retrieved from "http://e6.ijs.si/medusa/wiki/index.php?title=Weighted_Least_Squares_(WLS)&oldid=3200"