Difference between revisions of "Wave equation"
E6WikiAdmin (talk | contribs) |
E6WikiAdmin (talk | contribs) |
||
| (9 intermediate revisions by the same user not shown) | |||
| Line 4: | Line 4: | ||
__TOC__ | __TOC__ | ||
| − | |||
| − | |||
== 2D wave equation with Dirichlet boundary conditions == | == 2D wave equation with Dirichlet boundary conditions == | ||
| Line 114: | Line 112: | ||
== 2D time-domain acoustic wave propagation in heterogeneous media == | == 2D time-domain acoustic wave propagation in heterogeneous media == | ||
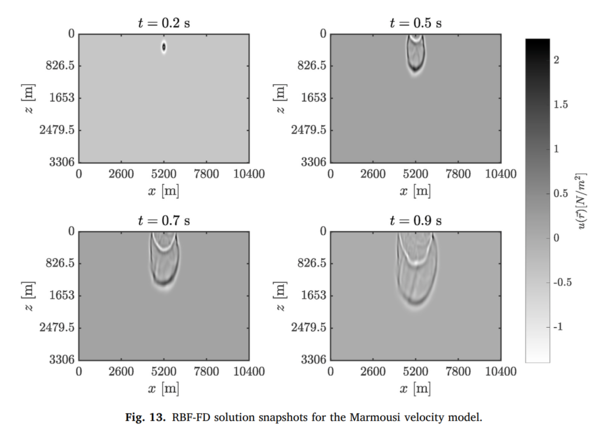
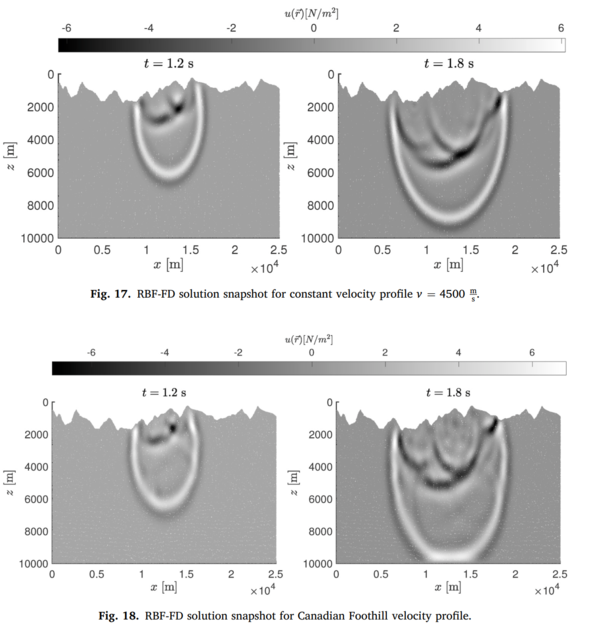
| + | We also solved wave equation in context of acoustic wave propagation in seismic modeling in the Earth’s subsurface (see related paper [https://e6.ijs.si/ParallelAndDistributedSystems/publications/62417923.pdf J. Močnik Berljavac, P. Mishra, J. Slak, G. Kosec; RBF-FD analysis of 2D time-domain acoustic wave propagation in heterogeneous media, Computers & Geosciences, 2021 [DOI: 10.1016/j.cageo.2021.104796]]. Some highlights from the paper | ||
| + | |||
| + | [[File:wave_mormosi.png|600px]] | ||
| − | + | [[File:wave_canadian.png|600px]] | |
Latest revision as of 20:50, 4 December 2022
Related papers
Contents
2D wave equation with Dirichlet boundary conditions
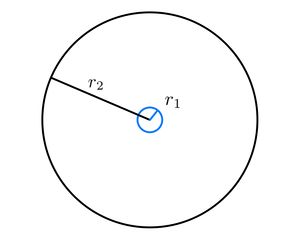
We are solving a problem analogous to a clamped circular membrane being forced to oscillate by fixing its centre to a rigid oscillating rod. The domain of calculation is for this reason an annulus bounded by the point of contact with the circular source in the centre and the clamped edge of the circular membrane.
Consider the time dependent solution to 2D wave equation on annulus shaped domain
\( \begin{align*} \frac{ \partial^2 u}{\partial t^2} &= c^2 \nabla^2 u &&\text{in } \Omega, \\ u(r,t=0)&=0 &&\text{in } \Omega, \\ u &= 0 &&\text{on } \partial \Omega_O,\\ u &= f(t) &&\text{on } \partial \Omega_I, \end{align*} \)
where $\partial\Omega_I$ denotes the inner and $\partial\Omega_O$ the outer boundary of the domain. Through the boundary condition on the inner boundary the source is introduced to the problem as a function of time
\( \begin{align*} f(t)= u_o \sin \omega_o t. \end{align*} \)
First the domain is constructed by subtracting a smaller circle domain from a larger one. Boundaries of the domain are populated in the same step.
1 // // identifier to be added to nodes on the inner boundary
2 int CENTRE = -10;
3
4 // build circle domain
5 BallShape<Vec2d> domain({0, 0}, outer_radius);
6 auto discretization = domain.discretizeBoundaryWithStep(dx);
7
8 // build source domain
9 BallShape<Vec2d> empty({0, 0}, inner_radius);
10 auto discretization_empty = empty.discretizeBoundaryWithStep(dx, CENTRE);
11
12 // substract the source domain
13 discretization -= discretization_empty;
Next the domain is populated with nodes in accordance with the desired density function. Once the domain is constructed and discretized, the support (neighborhood) of $n$ nodes is found for each node.
1 GeneralFill<Vec2d> fill;
2 fill.seed(fill_seed);
3 discretization.fill(fill, fill_density);
4
5 // find support
6 FindClosest find_support(n);
7 discretization.findSupport(find_support);
The density function "fill_density" takes as argument the coordinates inside the domain and returns the desired distance between neighboring nodes for that location. Now the domain preparation is complete, as domain is constructed and populated with nodes with support relations established. We continue by constructing the approximation engine.
1 WLS<Monomials<Vec2d>, GaussianWeight<Vec2d>, ScaleToClosest> approx(m - 1 , sigma);
As we are solving a time propagation problem implicitly, we will have to solve a system of equations for every time step. This is equivalent to solving a matrix equation. For this reason a space matrix is constructed. Next the wave equation is turned into code. Medusa encodes this information inside the just constructed matrix $M$. $E1$ and $E0$ represent the known solutions on previous two time steps.
1 SparseMatrix<double> M(domain_size, domain_size);
2 // Set equation on interior
3 for (int i : interior) {
4 -(v*v*dt*dt) * op.lap(i) + op.value(i)= 2*E1(i)-E0(i);
5 }
Same is done also for the boundary nodes. Since dirichlet boundary conditions are employed the values of the Right Hand Side ($rhs$) of matrix equation are just set to prescribed values ($0$ on the outer boundary and $f(t)$ on inner boundary).
1 // Set boundary conditions
2 for (int i : boundary) {
3 if (discretization.types()[i] == CENTRE) {
4 op.value(i) = A * std::sin(omega*dt*2); // step
5 } else {
6 op.value(i) = 0.0;
7 }
8 }
At each time step the matrix equation is solved using an Eigen linear equation solver, in this case, the BiCGStab algorithm. $E0$ and $E1$ are updated and the source is set to new value.
1 // Solve matrix system
2 VectorXd E2 = solver.solve(rhs);
3
4 // Update previous states
5 E0 = E1;
6 E1 = E2;
7
8 // Update rhs on interior
9 for (int i : interior) {
10 rhs(i) = 2*E1(i)-E0(i);
11 }
12
13 // Update rhs on boundary
14 for (int i : (discretization.types() == CENTRE)) {
15 rhs(i) = A * std::sin(omega*dt*tt); // step
16 }
The animation of solution is presented below. The complete exampe is avalible at wave_equation_2D.cpp.
2D time-domain acoustic wave propagation in heterogeneous media
We also solved wave equation in context of acoustic wave propagation in seismic modeling in the Earth’s subsurface (see related paper J. Močnik Berljavac, P. Mishra, J. Slak, G. Kosec; RBF-FD analysis of 2D time-domain acoustic wave propagation in heterogeneous media, Computers & Geosciences, 2021 [DOI: 10.1016/j.cageo.2021.104796]. Some highlights from the paper