Difference between revisions of "Determining the interior of the domain by oversampling the boundary"
(Created page with "Go back to Examples. Sometimes, the interior of a complex domain cannot be correctly determined from the discretized boundary, leading to points "leaking"...") |
|||
| Line 8: | Line 8: | ||
<syntaxhighlight lang="c++" line> | <syntaxhighlight lang="c++" line> | ||
| + | // Oversample the domain. | ||
| + | DomainDiscretization<Vec2d> oversampled_domain = shape.discretizeBoundaryWithStep(h / 5); | ||
| + | |||
// Construct the contains function. | // Construct the contains function. | ||
KDTree<Vec2d> contains_tree; | KDTree<Vec2d> contains_tree; | ||
| Line 24: | Line 27: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| − | The above procedure results in | + | Here we have decreased the spacing by 5 in the oversampled domain. For higher node densities, less oversampling also works. The above procedure results in |
[[File:oversampled_domain.png|400px]] | [[File:oversampled_domain.png|400px]] | ||
The whole example can be found as [https://gitlab.com/e62Lab/medusa/-/blob/dev/examples/poisson_equation TODO.cpp] along with the plot script that can be run by Matlab or Octave [https://gitlab.com/e62Lab/medusa/-/blob/dev/examples/poisson_equation TODO.m]. | The whole example can be found as [https://gitlab.com/e62Lab/medusa/-/blob/dev/examples/poisson_equation TODO.cpp] along with the plot script that can be run by Matlab or Octave [https://gitlab.com/e62Lab/medusa/-/blob/dev/examples/poisson_equation TODO.m]. | ||
Revision as of 15:27, 4 July 2022
Go back to Examples.
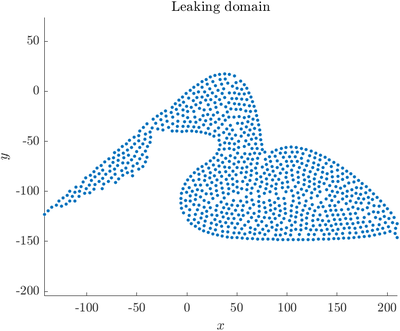
Sometimes, the interior of a complex domain cannot be correctly determined from the discretized boundary, leading to points "leaking" out of the domain. This can for example happen with the duck model shown in NURBS domains if it is sampled with small node density (big spacing $h$).
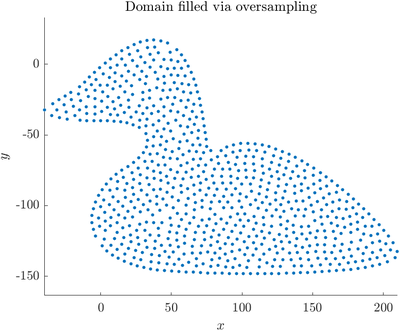
The easiest way to deal with this problem is to sample the boundary with a higher node density (smaller spacing $h$) and use this oversampled discretization when querying for the interior of the domain. This usage is supported by GeneralFill (see Positioning of computational nodes) and can be implemented by:
1 // Oversample the domain.
2 DomainDiscretization<Vec2d> oversampled_domain = shape.discretizeBoundaryWithStep(h / 5);
3
4 // Construct the contains function.
5 KDTree<Vec2d> contains_tree;
6 oversampled_domain.makeDiscreteContainsStructure(contains_tree);
7 auto contains_function = [&] (const Vec2d p) {
8 return oversampled_domain.discreteContains(p, contains_tree);
9 };
10
11 // Fill the boundary normally.
12 DomainDiscretization<Vec2d> domain = shape.discretizeBoundaryWithStep(h);
13
14 // Fill the interior with the contains function.
15 KDTreeMutable<Vec2d> tree;
16 GeneralFill<Vec2d> gf;
17 gf(domain, h, tree, contains_function);
Here we have decreased the spacing by 5 in the oversampled domain. For higher node densities, less oversampling also works. The above procedure results in
The whole example can be found as TODO.cpp along with the plot script that can be run by Matlab or Octave TODO.m.