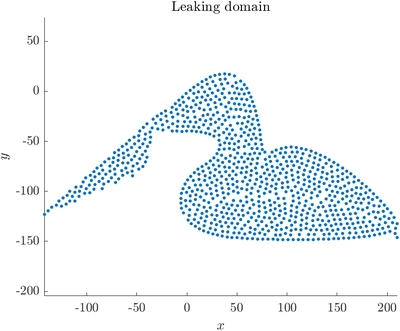
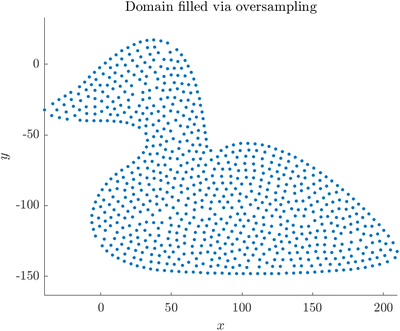
Determining the interior of the domain by oversampling the boundary

Go back to Examples.

Sometimes, the interior of a complex domain cannot be correctly determined from the discretized boundary, leading to points "leaking" out of the domain. This can for example happen with the duck model shown in NURBS domains if it is sampled with small node density (big spacing $h$).

The easiest way to deal with this problem is to sample the boundary with a higher node density (smaller spacing $h$) and use this oversampled discretization when querying for the interior of the domain. This usage is supported by GeneralFill (see Positioning of computational nodes) and can be implemented by:

 1 // Oversample the domain.
 2 DomainDiscretization<Vec2d> oversampled_domain = shape.discretizeBoundaryWithStep(h / 5);
 3 
 4 // Construct the contains function.
 5 KDTree<Vec2d> contains_tree;
 6 oversampled_domain.makeDiscreteContainsStructure(contains_tree);
 7 auto contains_function = [&] (const Vec2d p) {
 8     return oversampled_domain.discreteContains(p, contains_tree);
 9 };
10 
11 // Fill the boundary normally.
12 DomainDiscretization<Vec2d> domain = shape.discretizeBoundaryWithStep(h);
13 
14 // Fill the interior with the contains function.
15 KDTreeMutable<Vec2d> tree;
16 GeneralFill<Vec2d> gf;
17 gf(domain, h, tree, contains_function);

Here we have decreased the spacing by 5 in the oversampled domain. For higher node densities, less oversampling also works. The above procedure results in

The whole example can be found as inside_by_oversampling.cpp along with the plot script that can be run by Matlab or Octave inside_by_oversampling.m.