Difference between revisions of "Ghost nodes"
From Medusa: Coordinate Free Mehless Method implementation
| Line 1: | Line 1: | ||
| + | Go back to [[Medusa#Examples|Examples]]. | ||
| + | |||
See the [[Ghost nodes (theory)]] page for what ghost nodes and how they are used. We will use them in this example to reliably solver a 3D mixed Dirichlet and Neumann problem on an irregular domain. | See the [[Ghost nodes (theory)]] page for what ghost nodes and how they are used. We will use them in this example to reliably solver a 3D mixed Dirichlet and Neumann problem on an irregular domain. | ||
| Line 14: | Line 16: | ||
[[File:solution_ghost_example.png|600px]] | [[File:solution_ghost_example.png|600px]] | ||
| + | |||
| + | Go back to [[Medusa#Examples|Examples]]. | ||
Revision as of 09:31, 18 May 2019
Go back to Examples.
See the Ghost nodes (theory) page for what ghost nodes and how they are used. We will use them in this example to reliably solver a 3D mixed Dirichlet and Neumann problem on an irregular domain.
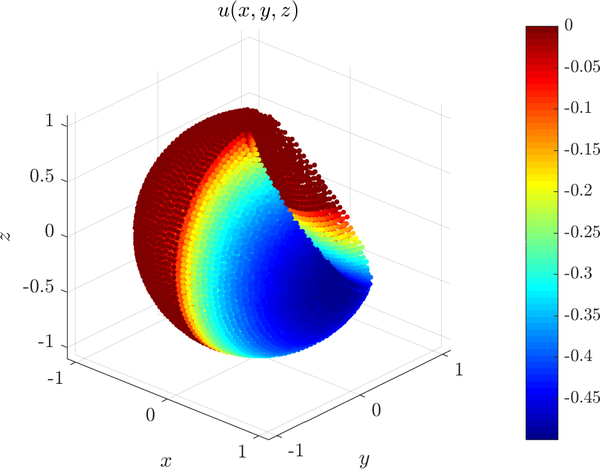
We will solve the problem
$\nabla^2 u = 1 \text{ in } \Omega, \quad \frac{\partial u}{\partial n} = 0 \text{ on } \partial \Omega_{+}, \quad u = 0 \text{ on } \partial \Omega_{-}$
where $\Omega = B(\boldsymbol{0}, 1) - B(\boldsymbol{1}, 1.5)$, $\partial \Omega_{+}$ is the part of the boundary with the nonnegative $x$ coordinate and $\partial \Omega_{-}$ the part of the boundary with negative $x$ coordinate.
TODO code, explanation, matrix.
The solution is shown below:
Go back to Examples.