Ghost nodes

Go back to Examples.

See the Ghost nodes (theory) page for what ghost nodes and how they are used. We will use them in this example to reliably solve a 3D mixed Dirichlet and Neumann problem on an irregular domain.

We will solve the problem

$\nabla^2 u = 1 \text{ in } \Omega, \quad \frac{\partial u}{\partial n} = 0 \text{ on } \partial \Omega_{+}, \quad u = 0 \text{ on } \partial \Omega_{-}$

where $\Omega = B(\boldsymbol{0}, 1) - B(\boldsymbol{1}, 1.5)$, $\partial \Omega_{+}$ is the part of the boundary with the nonnegative $x$ coordinate and $\partial \Omega_{-}$ the part of the boundary with negative $x$ coordinate.

The code below constructs ghost nodes and remembers the corresponding ghost node for each boundary node.

Range<int> gh = domain.addGhostNodes(dx, 0, neu);

It is equivalent to:

Range<int> gh(domain.size(), -1);  // Maps boundary nodes to their corresponding ghost nodes.
for (int i : neu) {  // Add ghost nodes for each Neumann boundary node
    gh[i] = domain.addNode(domain.pos(i) + dx*domain.normal(i), 0);   // add node with type 0
}

When assembling the system, we write two equations for each Neumann node. One is the Neumann BC and is written in the row corresponding to the boundary node. The other is the fact that the PDE also holds at the boundary node, but we write that equation in the row, corresponding to the ghost node.

for (int i : interior) {
    op.lap(i) = 1.0;  // Equation
}
for (int i : dir) {
    op.value(i) = 0.0;  // Dirichlet
}
for (int i : neu) {
    op.neumann(i, domain.normal(i)) = 0.0;  // Neumann
    // Equation holds also on the boundary, write it in the row corresponding to the ghost node.
    op.lap(i, gh[i]) = 1.0;
}

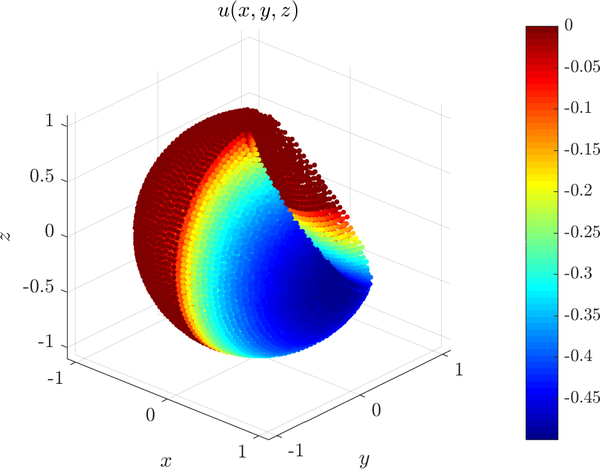
The system is then solved as usual. The solution (without the ghost nodes) is shown below:

The code is available as poisson_mixed_3D_ghost.cpp in the Medusa examples.

Go back to Examples.