Realistic 3D models

Medusa is not meant to deal with complex 3D geometry - we support balls, cuboids, and their differences, unions, translations and rotations. More general 2D shapes can be described by polygons, which are also included in Medusa. For more general 3D objects, the geometric algorithms become more complex and it makes sense to leverage third-party libraries.

Formats, software, and other resources

A good library in c++ is CGAL ([1]), that we can use to work with surface meshes: https://doc.cgal.org/latest/Surface_mesh/index.html CGAL can usually be installed with apt-get install libcgal-dev or similar. The Qt dependency is not necessary, but can be useful for easier visualization without exporting to an external program.

Polyhedrons are solid bodies with polygonal faces, and their surface forms a closed mesh. CGAL can work also with surfaces meshes that are not closed, but for PDE solving in 3D bodies, we assume them to be closed (or watertight) and triangular. Polyhedron data is usually stored in a separate file with many different formats available. Some of the formats actually store the polyhedron data (including how faces are connected) and some only store the faces. By default, CGAL reads OFF files [2], and these files can also be easily viewd by geomview [3], also trivially installable on most Linux systems. OFF files include an option to specify the color of each face, which can be used to identify different surface regions.

Other formats include STL, PLY and OBJ, and other proprietary formats. Some of these formats are more appropriate than others. Notably STL, while very common, can be problematic, as it does not include connections between faces, bit only a list of triangles, from which the polyhedron must first be reconstructed. This can be done directly in CGAL by using CGAL::Polygon_mesh_processing::polygon_soup_to_polygon_mesh, through an intermediate program, like Meshlab https://www.meshlab.net/, or through an online converter, such as https://cadcook.com/ply-off/. Note that it is not necessary that any of these conversions work, since STL file can represent an object with holes in the surface mesh or other degenerated objects. PLY files on the other hand do represent surface meshes, and can be read in CGAL (or easily converted to OFF) [4]. Similar hold for OBJ files, although, these files can contain many other types of objects besides polygon meshes. CGAL includes readers and writers for OFF, PLY, OBJ and STL formats [5], and the default cin >> operator expects an OFF file. Further demos for polyhedron IO are available in the CGAL repo [6].

PLY, OFF and STL files can also be read with Matlab, but require (short) external functions, available at [7], see Function/IO. These return a list of vertices and faces, that can be plotted with patch or trisurf after constructing the triangulation.

Obtaining models can be somewhat difficult, as this files are often used to store general 3D objects for rendering. Here is a list of common 3D models (not all of which are polyhedrons): https://github.com/alecjacobson/common-3d-test-models. Specifically, an altered Stanford bunny model (made watertight) in OFF format can be found here [8]. Googling with keywords "polyhedron", "surface mesh", "watertight", "closed", "OFF" or "PLY" might help.

General models (often STL files) can be downloaded from https://grabcad.com/ (after registering). Usually it is simplest to inspect them with Meshlab and also use it to save files as OFF.

This shows the bunny.off file referenced above open in Meshlab.

Meshlab can also be used to fill holes, clean meshes and color faces. See the Filters / Remeshing or the Filters / Color menu. Meshlab also colors vertices, and when saving, one can choose to save only the face colors. Saving also the vetor files with cause the file to be saved as COFF format, which also supports vertex colors.

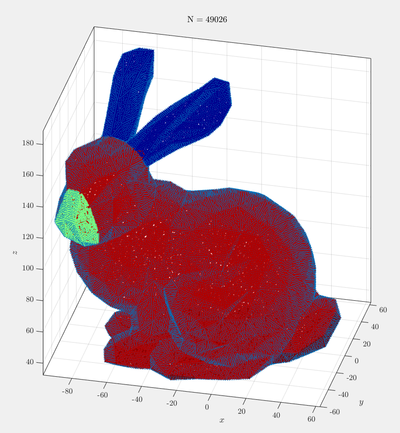
Below is an example of colored bunny. The colors can be used to identify surface regions where different boundary conditions should be applied.

Working with 3D models in Medusa

We assume that an OFF file has been successfully obtained, in this example we will use the bunny.off file from https://github.com/OpenGP/OpenGP/blob/master/data/bunny.off that was colored as the picture above. To work with Medusa, we can make a generic PolyhedronShape, that can also be used with other existing shapes (translations, boolean operations, etc).

This is done by inheriting from DomainShape and defining the required methods. Notably, CGAL is use to get a proper implementation of contains method, that is needed for filling the domain. CGAL is also used to get the bounding box, and to store the surface mesh in an easily traversable data structure. Note that the polyhedron, represented in the OFF file is considered to be the exact domain, which is then discretize with meshless techniques. The mesh is used only to define the domain, and is considered fixed and final. Discretizations can (and usually should) be smaller than.

Below is a picture of the bunny OFF model with surface nodes of various types, as defined by the face colors, along with the surface normals.

The PolytopeShape (a dimension independent version of PolyhedronShape and PolygonShape) can be used to work with OFF files. Otherwise, the solution procedure is as usual.

 1 #include <medusa/bits/domains/PolyhedronShape.hpp>  // This must be included separately.
 2 ...
 3 
 4 int main() {
 5     std::string filename = "bunny.off";
 6     PolytopeShape<Vec3d> bunny = PolytopeShape<Vec3d>::fromOFF(filename);
 7 
 8     double dx = 2.5;
 9     DomainDiscretization<Vec3d> domain = bunny.discretizeBoundaryWithStep(dx);
10     GeneralFill<Vec3d> fill; fill.seed(0);
11     fill(domain, dx);
12 
13     ... // The usual.
14 
15     for (int i : domain.interior()) {
16         0.1*op.grad(i, -1) + 2.0*op.lap(i) = -1.0;
17     }
18     for (int i : domain.boundary()) {
19         op.value(i) = 0.0;
20     }
21 
22     Eigen::BiCGSTAB<decltype(M), Eigen::IncompleteLUT<double>> solver;
23     solver.preconditioner().setDroptol(1e-4);
24     solver.preconditioner().setFillfactor(20);
25     solver.compute(M);
26     ScalarFieldd u = solver.solve(rhs);
27 
28 }

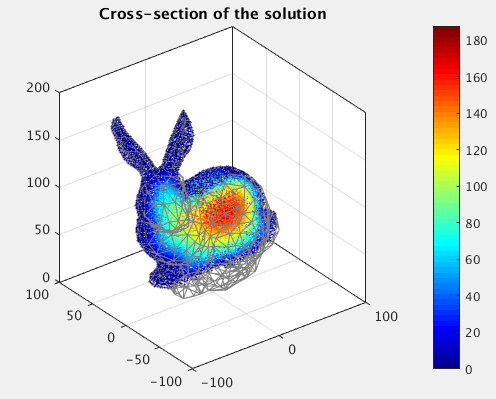
The solution is shown below: