Radial basis function-generated finite differences (RBF-FD)
Related papers
This page describes the computation of RBF-FD weight augmented with polynomials. See also Computation of shape functions and Meshless Local Strong Form Method (MLSM) for a more general discussion.
RBF-FD
$ \newcommand{\R}{\mathbb{R}} \newcommand{\T}{\mathsf{T}} \renewcommand{\L}{\mathcal{L}} \renewcommand{\b}{\boldsymbol} \newcommand{\n}{\b{n}} \newcommand{\x}{\b{x}} \newcommand{\w}{\b{w}} \newcommand{\eps}{\varepsilon} \newcommand{\lap}{\nabla^2} \newcommand{\dpar}[2]{\frac{\partial #1}{\partial #2}} $
Approximations of partial differential operators are the core of strong form meshless procedures. Consider a partial differential operator $\L$ at a point $\x_c$. Approximation of $\L$ at a point $\x_c$ is sought using an ansatz \begin{equation} \label{eq:approx} (\L u)(\x_c) \approx \sum_{i=1}^{n} w_i u(\x_i). \end{equation} Here $\x_i$ are the neighboring nodes of $\x_c$ which constitute its stencil, $w_i$ are called stencil weights, $n$ is the stencil size and $u$ is an arbitrary function.
This form of approximation is desirable, since operator $\L$ at point $\x_c$ is approximated by a linear functional $\w_\L (\x_c)$, assembled of weights $\w_i$ \begin{equation} \label{eq:approx-vec} \L|_{\x_c} \approx \w_\L (\x_c)^\T \end{equation} and the approximation is obtained using just a dot product with the function values in neighboring nodes. The dependence of $\w_\L (\x_c)$ on $\L$ and $\x_c$ is often omitted and written simply as $\w$.
To determine the unknown weights $\w$, equality of \eqref{eq:approx} is enforced for a given set of functions. A natural choice are monomials, which are also used in FDM, resulting in the Finite Point Method.
In the RBF-FD discretization the equality is satisfied for radial basis functions $\phi_j$. Each $\phi_j$, for $j = 1, \ldots, n$ corresponds to one linear equation \begin{equation} \sum_{i=1}^{n} w_i \phi_j (\x_i) = (\L \phi_j)(\x_c) \end{equation} for unknowns $w_i$. Assembling these $n$ equations for into matrix form, we obtain the following linear system: \begin{equation} \label{eq:rbf-system} \begin{bmatrix} \phi(\|\x_1 - \x_1\|) &\cdots & \phi(\|\x_n - \x_1\|) \\ \vdots & \ddots & \vdots \\ \phi(\|\x_1 - \x_n\|) &\cdots & \phi(\|\x_n - \x_n\|) \end{bmatrix} \begin{bmatrix} w_1 \\ \vdots \\ w_n \end{bmatrix} = \begin{bmatrix} (\L\phi(\|\x-\x_1\|))|_{\x=\x_c} \\ \vdots \\ (\L\phi(\|\x-\x_n\|))|_{\x=\x_c} \\ \end{bmatrix}, \end{equation} where $\phi_j$ have been expanded for clarity. The above system will be written more compactly as \begin{equation} \label{eq:rbf-system-c} A \w = \b \ell_\phi. \end{equation} The matrix $A$ is symmetric, and for some $\phi$ even positive definite.[1] The Solving linear systems page has more details on numerical techniques for solving.
Monomial augmentation
Using approximations that only contain RBF can lead to stability issues with conditioning under refinement or failure to converge due to stagnation errors. To improve accuracy and convergence, the approximation can be augmented with polynomials.
Let $p_1, \ldots, p_s$ be polynomials forming the basis of the space of $d$-dimensional multivariate polynomials up to and including total degree $m$, with $s = \binom{m+d}{d}$.
Since enforcing exactness of \eqref{eq:approx} for additional function would result in an overdetermined system, these additional constraints are enforced by extending \eqref{eq:rbf-system-c} as \begin{equation} \label{eq:rbf-system-aug} \begin{bmatrix} A & P \\ P^\T & 0 \end{bmatrix} \begin{bmatrix} \w \\ \b \lambda \end{bmatrix} = \begin{bmatrix} \b \ell_{\phi} \\ \b \ell_{p} \end{bmatrix}\!\!,\ P = \begin{bmatrix} p_1(\x_1) & \cdots & p_s(\x_1) \\ \vdots & \ddots & \vdots \\ p_1(\x_n) & \cdots & p_s(\x_n) \\ \end{bmatrix}\!\!,\ \b \ell_p = \begin{bmatrix} (\L p_1)|_{\x=\x_c} \\ \vdots \\ (\L p_s)|_{\x=\x_c} \\ \end{bmatrix} \end{equation} where $P$ is a $n \times s$ matrix of polynomials evaluated at stencil nodes and $\b \ell_p$ is the vector of values assembled by applying considered operator $\L$ to the polynomials at $\x_c$.
Note that the equation $P^\T \w = \b \ell_p$ contains exactly exactness constraints for $p_j$. However, the introduction of parameters $\lambda_j$ causes \eqref{eq:approx} to not be exact for $\phi_i$ anymore. In fact, is was shown to be equivalent to the following constrained minimisation problem \begin{equation} \min_{\w} \left(\frac{1}{2} \w^\T A \w - \w^\T \b \ell_{\phi}\right), \text{ subject to } P^\T \b w = \ell_{p} \end{equation} and parameters $\b \lambda$ can be interpreted as Lagrangian multipliers.
Weights obtained by solving \eqref{eq:rbf-system-aug} are taken as approximations of $\L$ at $\x_c$, while values $\b \lambda$ are discarded.
Example
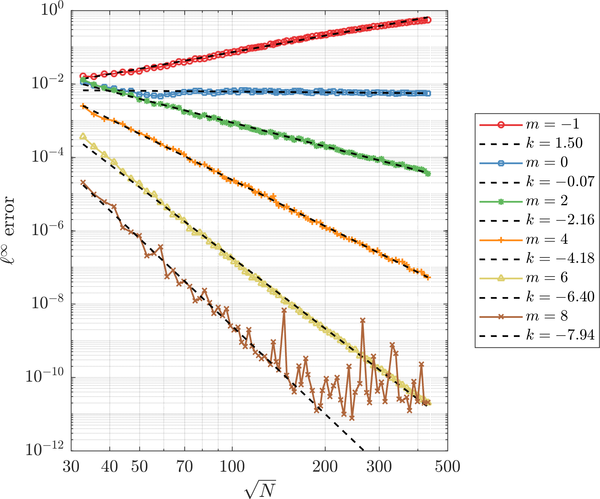
The $\ell_\infty$ error of solving Poisson equation on a unit ball using RBF-FD with PHS (Polyharmonic spline) $\phi(r) = r^3$ with various orders of monomial augmentation is shown below. [2]
Exactness constraints for monomials often produce high-order methods, since local error of function approximation is small (imagine that the Taylor expansion is exact up to a high order).