Ghost nodes (theory)
Ghost nodes are a technique for discretizing (mostly) Neumann boundary conditions in PDEs. See the example.
Introduction
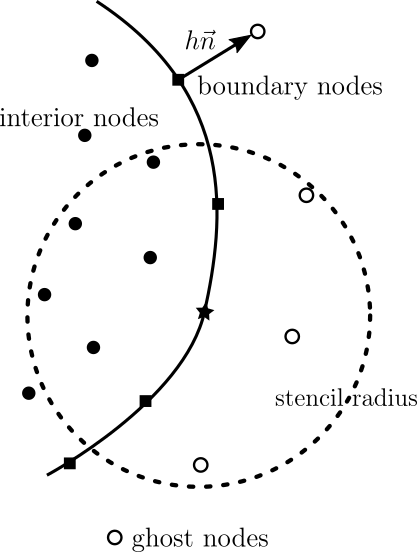
Ghost nodes are a technique used for discretizing Neumann boundary conditions in FDM. To be able to use the central difference for first derivative, additional point, called ghost point, is introduced outside the domain boundary. The unknown function value at the ghost node is added as a variable. At the boundary node, the Neumann condition is enforced, as well as the equation itself (two equations for two unknowns, the ghost and the boundary function value).
Meshless setting (implicit)
Consider the problem $\mathcal{L}u = f$ with Neumann boundary conditions $\frac{\partial u}{\partial n} = g$ on some portion $\Gamma_1$ of the boundary and Dirichlet conditions $u = u_0$ on portion $\Gamma_2$. Denote the number of internal nodes with $N_i$, number of Neumann boundary nodes with $N_n$ and number of Dirichlet boundary nodes with $N_d$. The total number of nodes $N$ is equal to $N = N_i + N_n + N_d$ and so is the number of unknowns, representing solution values at these nodes.
For each Neumann node $p$, additional ghost or fictious nodes are placed outside the domain, as seen in the figure on the right. This is usually done so that one ghost node is added for each boundary node, spaced $h$ away in the normal direction, where $h$ is the local nodal spacing. This increases the number of nodes and unknowns by $N_n$. Stencils and stencil weights are computed as before, and ghost nodes are included in the stencils. For each node $p_j$ denote the indices of its stencil nodes by $I_j$. We will denote the computed stencil weights for operators with $w_\mathcal{L,j}$ and $w_{\frac{\partial }{\partial n},j}$.
We have the same equations as before:
- $N_i$ for interior nodes: $w_{\mathcal{L},j} \cdot \boldsymbol{u}_{I_j} = f_j$
- $N_d$ for Dirichlet nodes: $u_j = u_{0,j}$
- $N_n$ for Neumann nodes: $w_{\frac{\partial }{\partial n},j} \cdot \boldsymbol{u}_{I_j} = g_j$
Additional $N_n$ equations for ghost nodes are required. They are obtained by stating that the PDE itself must also hold in the boundary node, i.e., we add
- additional $N_n$ equations for Neumann nodes: $w_{\mathcal{L},j} \cdot \boldsymbol{u}_{I_j} = f_j$.
Note that no requirements about the PDE or BCs are made in the ghost nodes, they are simply involved as stencil nodes in the two equations for Neumann nodes (and possibly others).
All these equations are assembled in a sparse matrix which is solved and values obtained for ghost nodes can be neglected.
Additionally, more than one layer of ghost nodes can be added and additional equations on the boundary are needed. Sometimes, equations $\mathcal{L}^2 u = \mathcal{L}f$, etc... are used.
For an example of ghost nodes generation and use in Medusa see the Ghost nodes example.
Explicit version
When explicit time stepping is used, Neumann boundary conditions and ghost nodes are more difficult to implement. We assume that the values of the interior in the $n$-th iteration are already known and denoted by $u_j^n$, as well as the boundary and ghost values from the previous iteration $u_j^{n-1}$.
Consider a boundary node $p_j$ with an associated ghost node $p_{\gamma_j}$ and stencil indices $I_j = \{j, \gamma_j, i_1, \ldots, i_{n-2}\}$. Denote the stencil weights at $p_j$ for $\mathcal{L}$ as $w_{\mathcal{L},j}$ and for $\frac{\partial }{\partial n}$ as $w_{\frac{\partial }{\partial n},j}$.
We have two equations at this node:
$$\sum_{i \in I_j} w_{\mathcal{L},j,i} u_i^{n} = f_j$$ $$\sum_{i \in I_j} w_{\frac{\partial }{\partial n},j, i} u_i^{n} = g_j$$
A system of these $2N_n$ equations can be solved in each iteration to obtain the next values of ghost and boundary nodes.
Furthermore, this system can be made explicit using single step of Gauss-Seidel iteration on a single step. We use the second equation to compute the new value of $u_{\gamma_j}$ and the first to compute the new value of $u_j$.
For each ghost node $p_{\gamma_j}$: $$u_{\gamma_j}^n = \frac{1}{w_{\frac{\partial }{\partial n},j,\gamma_j}} \left[ g_j - w_{\frac{\partial }{\partial n},j,j} u_j^{n-1} - \sum_{k=1}^{n-2}w_{\frac{\partial }{\partial n},j,i_k} u_{i_k}^{n|n-1} \right]$$
For each boundary node $p_j$: $$u_{j}^n = \frac{1}{w_{\mathcal{L},j,\gamma_j}} \left[ f_j - w_{\mathcal{L},j,\gamma_j} u_{\gamma_j}^{n} - \sum_{k=1}^{n-2}w_{\mathcal{L},j,i_k} u_{i_k}^{n|n-1} \right]$$
The time index $n|n-1$ refers to either $n$ it the value of node $i_k$ has already been computed in this iteration (e.g. it is an internal node or already computed ghost or boundary node) or $n-1$ if the value is now known yet.
We are assuming that the stencil weight of the ghost node is nonzero in the discretization of the Neumann BC and that the weight of the boundary noe is nonzero in the discretization of $\mathcal{L}$. If this is not the case, the equations need to be rearranged differently.