Adaptivity
Go back to Examples.
Related papers
Contents
Solutions to many physical problems governed by partial differential equations (PDE) often significantly vary in magnitude throughout the problem domain. Although in some special cases the areas with high error are known in advance, in general the error distribution is unknown beforehand. Adaptive techniques for solving PDEs are a standard way of dealing with this problem, where problematic regions are iteratively refined. A step further is automatic adaptivity, where problematic regions are chosen automatically using an error indicator and then refined, until certain error threshold is reached. Below, we show some examples of fully automatic adaptivity in Medusa.
Basic concept
The adaptive methodology in this paper behaves similarly to "remeshing" used commonly in FEM. Some initial (possibly variable) nodal spacing $h^0$ is chosen, as well as its lower and upper bounds $h_L$ and $h_U$, respectively. Domain $\Omega$ is filled with nodes, conforming to $h^0$ and the solution $u^0$ is obtained. An error indicator is employed to determine which nodes should be (de)refined and the nodal density $h^0$ is altered appropriately. This adaptive cycle below is repeated until the convergence criterion is met. The procedure on $j$-th iteration is written in more detail below:
- Fill $\Omega$ with nodes conforming to $h^j$.
- Solve the problem to obtain $u^j$.
- Compute the error indicator values $\varepsilon_i^j$ for each node $p_i$.
- If the mean of $\varepsilon_i^j$ is below some tolerance $\varepsilon$ return $u^j$ as the solution and stop.
- Adapt $h^j$ to obtain $h^{j+1}$.
More details can be found in our paper [1].
Node density adaptation
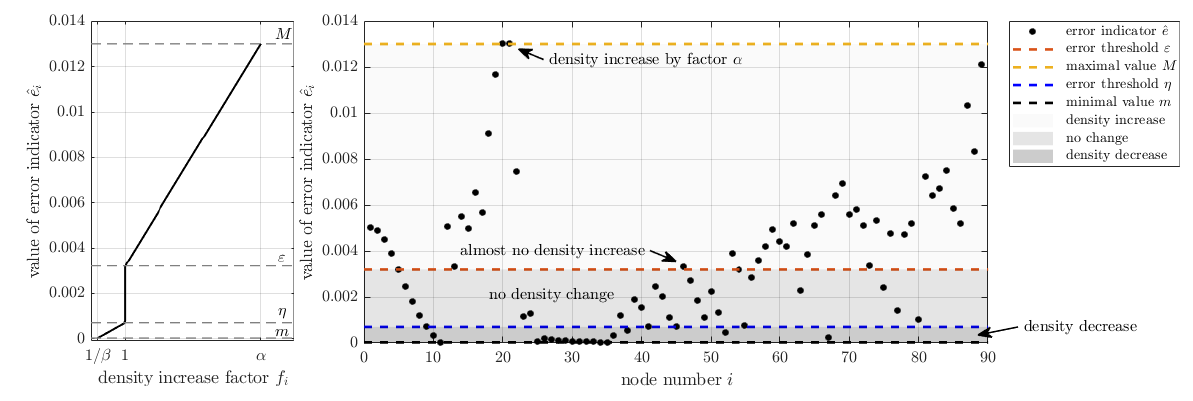
The existing nodal spacing function $h^j$ is evaluated at nodes $p_i$ to obtain values $h_{i,j} = h^j(p_i)$ . These values $h_{i,j}$ are modified by a density factor $f_i$ as $$ h_{i,j+1} = \min(\max(h_{i,j} / f_i, h_L(p_i)), h_U(p_i)), $$ where density factor $f_i$ is computed as $$ f_i = \begin{cases} 1 + \frac{\eta - \varepsilon_i}{\eta - m} (\frac{1}{\beta} - 1), & \varepsilon_i \leq \eta, \quad \text{i.e. decrease the density} \\ 1, & \eta < \varepsilon_i < \varepsilon, \quad \text{i.e. no change in density}\\ 1 + \frac{\varepsilon_i - \varepsilon}{M - \varepsilon} (\alpha - 1), & \varepsilon_i \geq \varepsilon, \quad \text{i.e. increase the density} \end{cases} $$ and $\alpha$ represents the refine aggressiveness, $\beta$ the derefine aggressiveness, $\varepsilon$ the refinement threshold, $\eta$ the derenfinement threshold, and $m = \min_i \varepsilon_i$ is the minimal and $M = \max_i \varepsilon_i$ is the maximal value of the error indicator. Note that setting $\alpha=1$ or $\beta=1$ disables refinement and derefinement, respectively.
This adaptation is illustrated in the figure below.
Error indicators
The work on error indicators is ongoing. For now, we use an ad hoc error indicator $$\varepsilon_i = \operatorname{std}_{j \in I_i}(u_j),$$ which represents the standard deviation of function values over all stencil nodes of a given node $p_i$.
Numerical exmaples
Below are several numerical examples where adaptivity has been tested or used to obtain solutions.
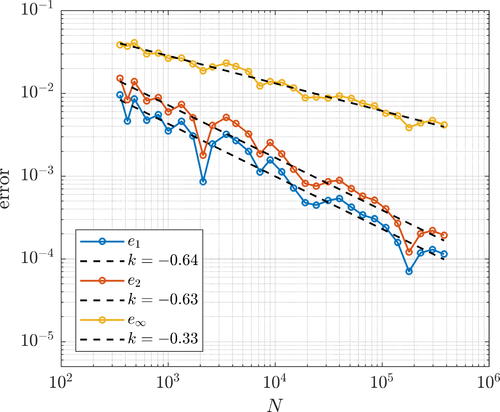
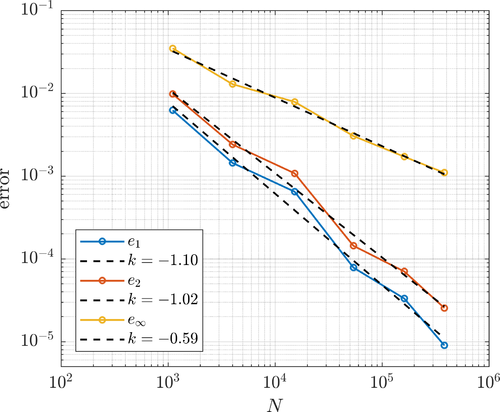
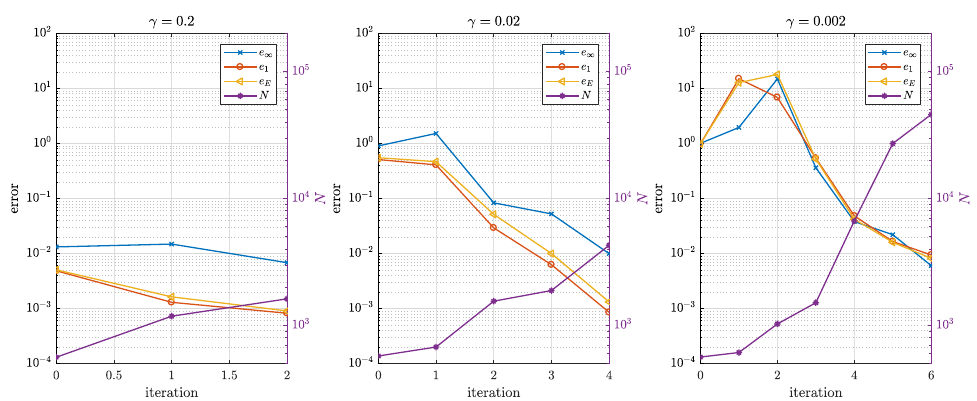
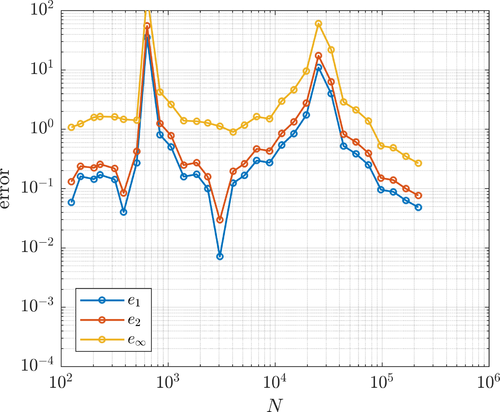
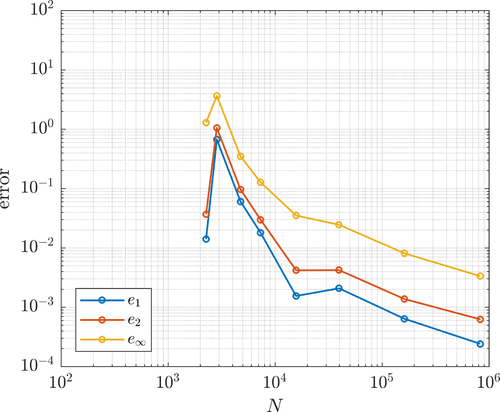
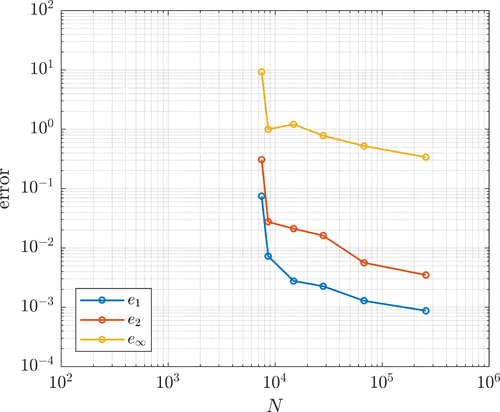
The errors $e_1$, $e_2$, $e_\infty$ and $e_E$ refer to relative discrete $L^1$, $L^2$, $L_\infty$ and energy norm errors, respectively. These are evaluated in the computation nodes or on a denser grid by reinterpolation.
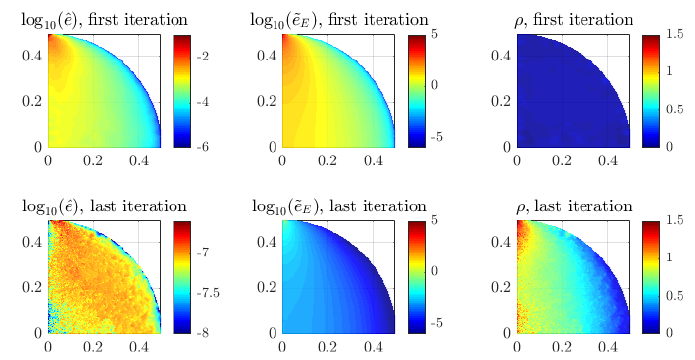
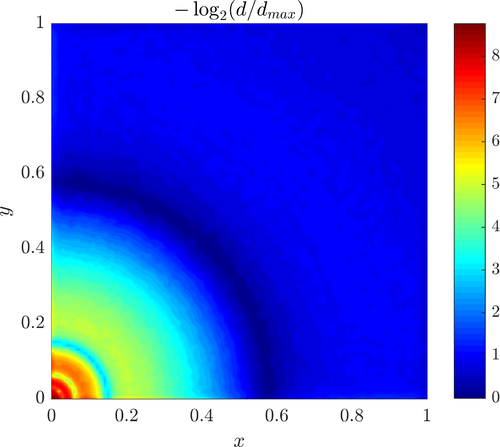
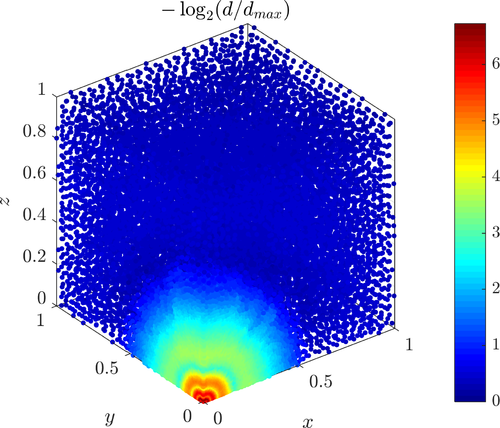
Relative node density $\rho_i$ is calculated by computing the distances $d_i$ from each node to its closest neighbour and expressing them as the logarithmic ratio against the maximal distance: $\rho_i = -\log_2(d_i / \max_j d_j)$.
L shaped domain
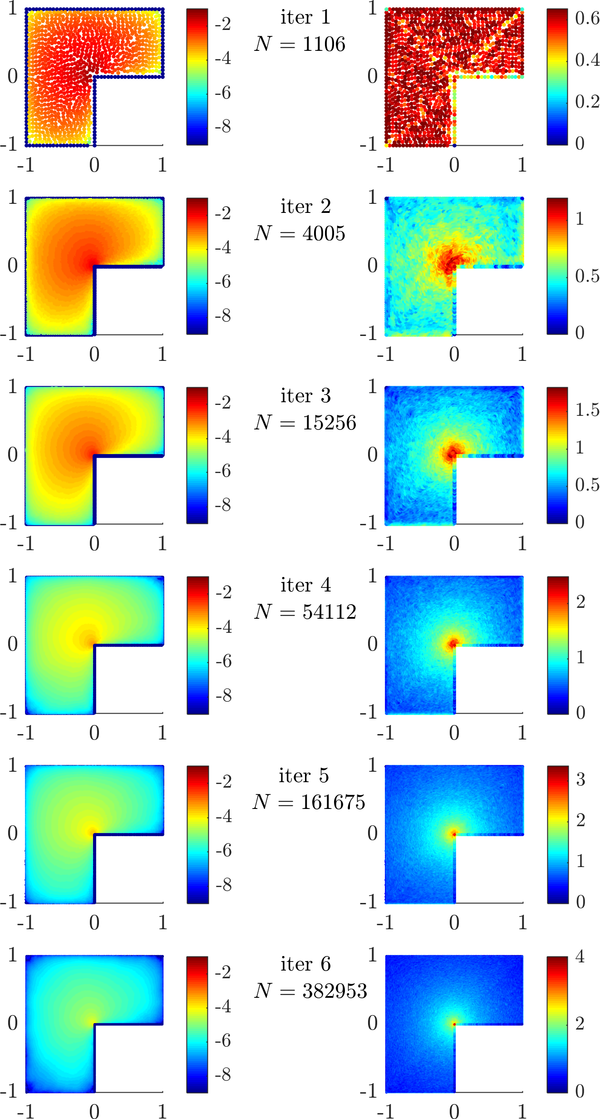
The L shaped domain problem is defined on $\Omega = [-1, 1]^2 \setminus [0, 1] \times [-1, 0]$. The Laplace problem $\nabla^2u = 0$ with the solution $u = r^{\frac{2}{3}} \sin(\frac{2}{3}\theta)$ given in polar coordinates.
BF-FD method with Polyharmonic splines augmented with monomials up to and including 2nd order was used to approximate the differential operators. The stencils for each node were chosen by simply selecting the closest $n=15$ nodes. The resulting sparse system was solved using the Intel ® MKL Pardiso sparse solver. Both uniform and fully adaptive refinement was tested. The adaptive procedure was run with $\alpha=3$, $\varepsilon = 10^{-2}$, $\beta=1$ and $\eta=0$.
The errors under uniform (left) and adaptive (right) refinement are shown below.
The error (left) and the nodal density (right) during the adaptive iteration are shown below.
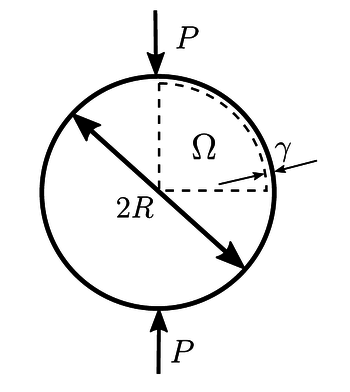
Disk under stress
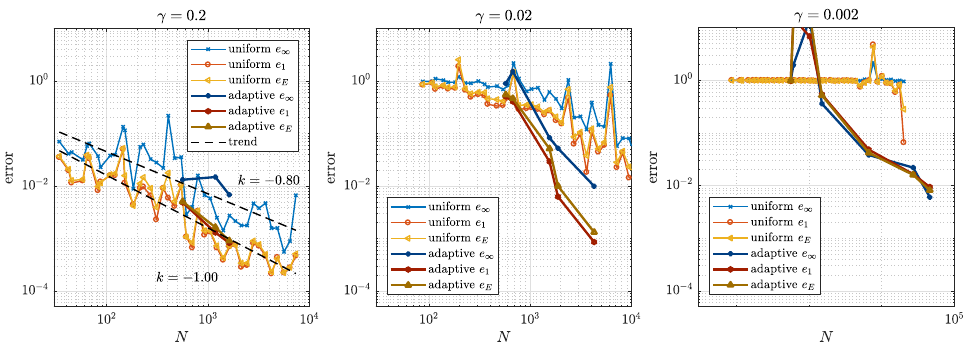
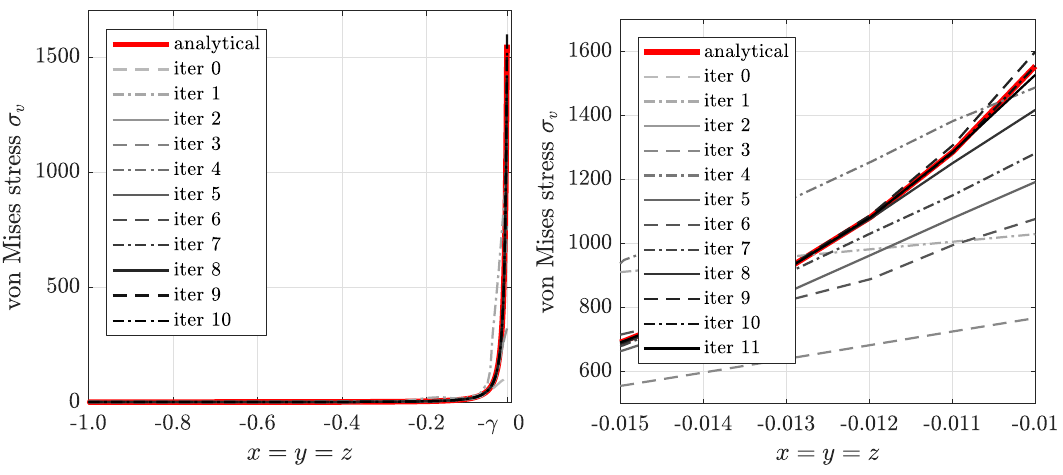
The next case is disk under pressure case from Linear elasticity solving the Caucy-Navier equation of Solid Mechanics. The problem considers one quarter of the disk illustrated below by the domain $\Omega$. The spacing $\gamma$ represents the distance from the singularity.
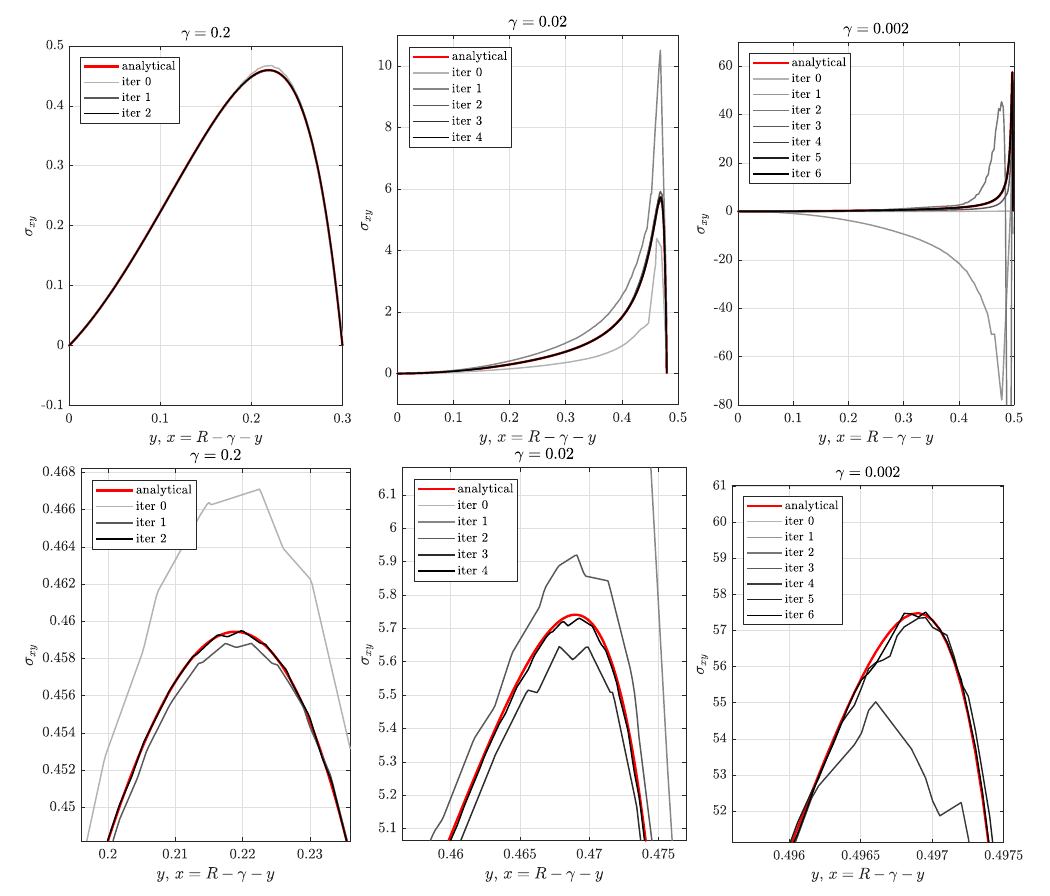
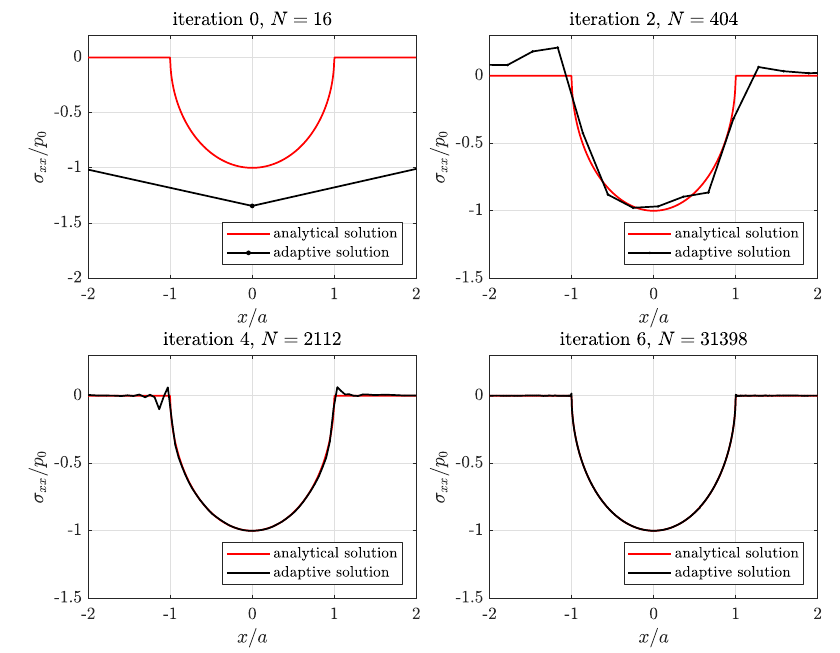
Computed $\sigma_{xy}$ stress profiles for three considered cases. The lower three images show close-ups of the computed peaks.
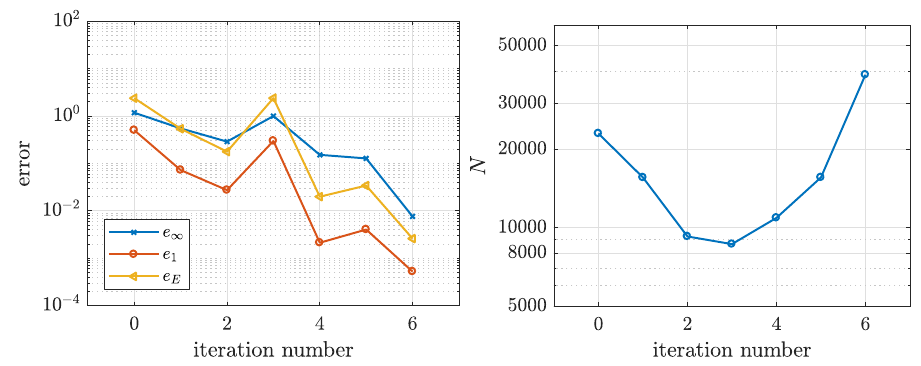
Error of the numerical solution of the compressed disk problem during adaptive iteration.
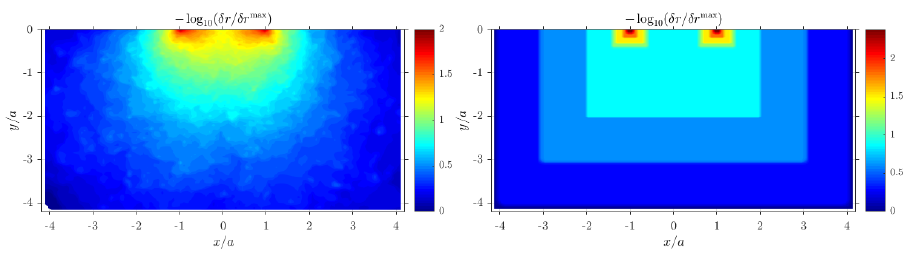
Error indicator value and node density in the last iteration.
Comparison of uniform and adaptive refinement.
Hertzian contact
See Hertzian_contact for the description.
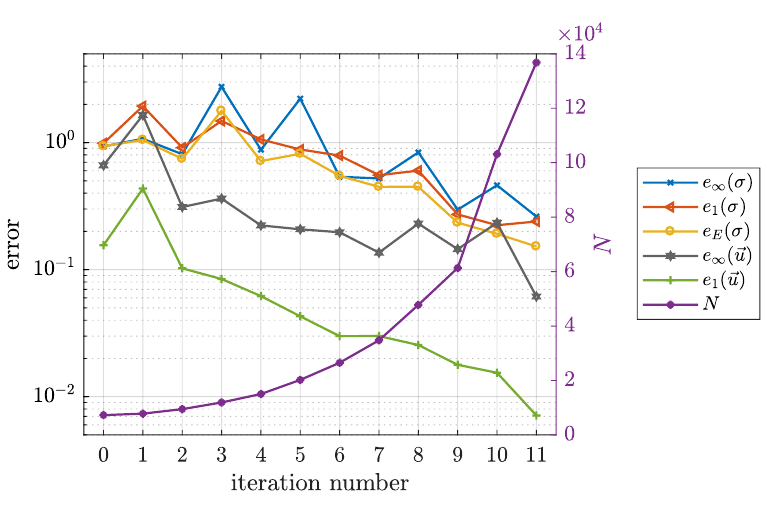
Errors and node counts during adaptive iteration for the solution of the Hertzian problem. Observe the initial decrease due to derefinement.
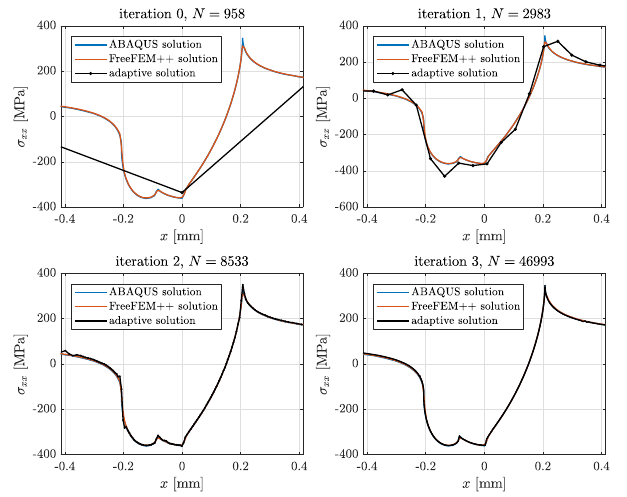
Top surface stress profiles during the iteration. Only even iterations are shown for brevity.
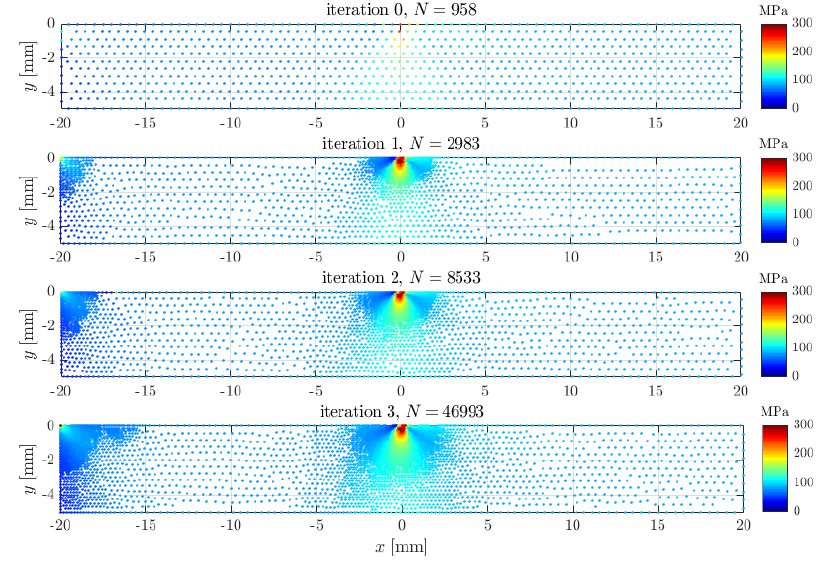
Comparing adaptive (left) and manual (right) nodal distributions densities for the Hertzian problem. The manual density was used in the refinement paper[2].
Fretting fatigue contact
See Fretting fatigue case for the description.
Surface traction $\sigma_{xx}$ under contact in four subsequent adaptive iterations during the solution of the fretting fatigue problem.
Nodes of four subsequent adaptive iterations during the solution of the fretting fatigue problem, coloured by von Mises stress.
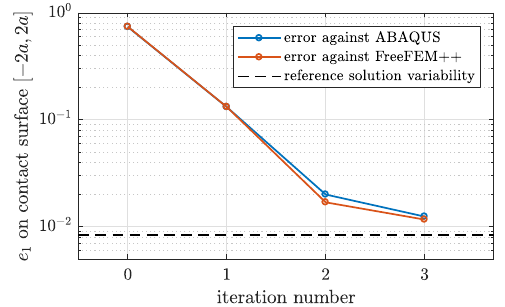
Error of surface traction using two reference solutions.
Bousinesq's problem
See Linear_elasticity#Point_contact_3D for more details.
Error with respect to the number of nodes in the adaptive iteration of the solution of the Boussinesq's problem. The right axis shows the number of computational nodes.
Stress profiles along the body diagonal from $[-1, -1, -1]$ to $[-\gamma, -\gamma, -\gamma]$ in adaptive iteration when solving the Boussinesq's problem.
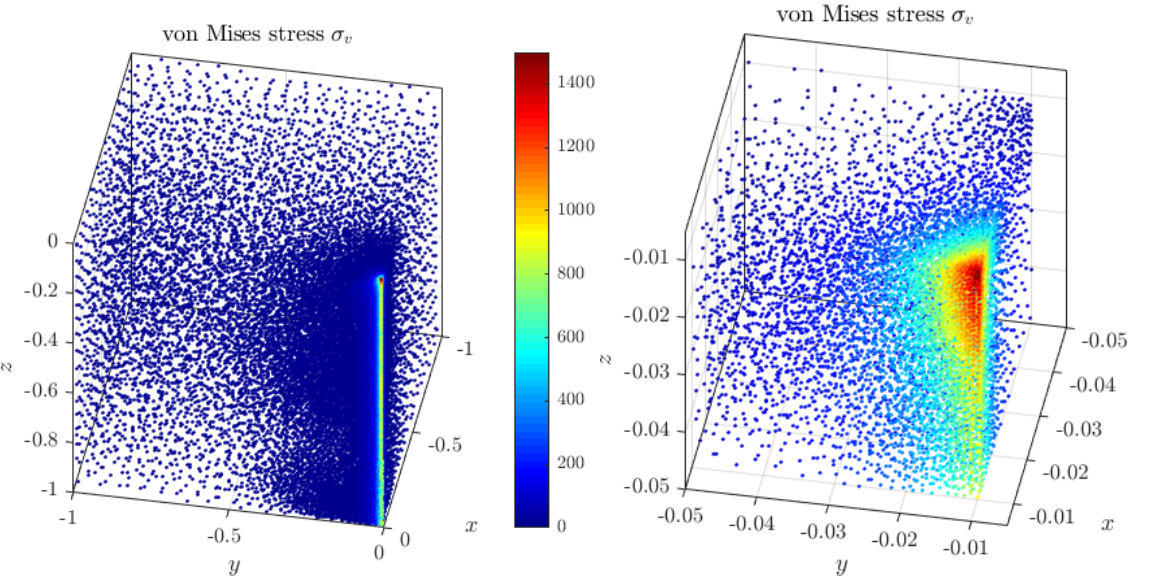
The obtained solution in the final iteration with an enlarged portion around the contact area. Both solutions are plotted only in the computation nodes to also show the final nodal distribution. Nodes are coloured proportional to computed values of von Mises stress.
Helmholz equation
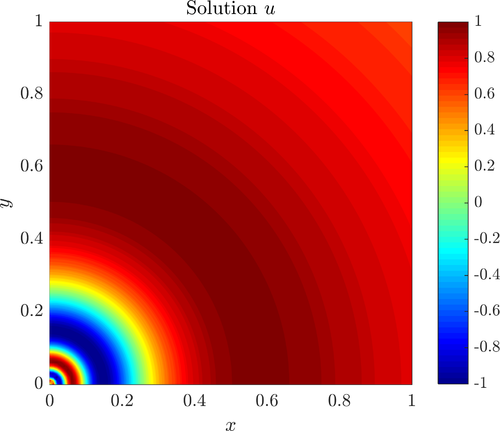
The equation $\nabla^2 u + \frac{1}{(\alpha+r)^4} u = f$ with the solution $u = sin(\frac{1}{\alpha+r})$ is solved adaptively. The value $\alpha = \frac{1}{5\pi}$ was used and the right hand side $f$ was computed from $u$.
Error under uniform (left) and adaptive (right) refinement.
Solution and the nodal density in the final iteration.
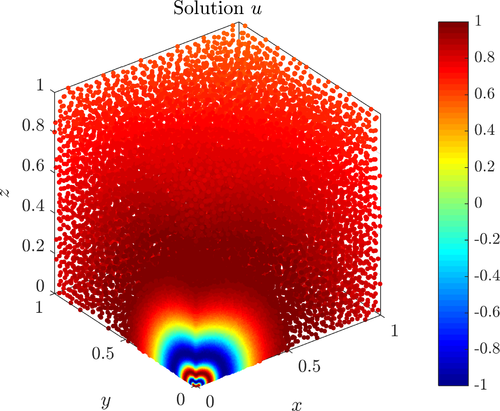
Error under adaptive refinement for the 3D equation.
Solution and the nodal density in the final iteration of the 3D solution.
References
- ↑ Slak, J., & Kosec, G. Adaptive radial basis function‐generated finite differences method for contact problems. International Journal for Numerical Methods in Engineering, 2019.
- ↑ Slak, J., & Kosec, G. (2019). Refined Meshless Local Strong Form solution of Cauchy–Navier equation on an irregular domain. Engineering analysis with boundary elements, 100, 3-13.
Go back to Examples.