1D MLSM and FDM comparison

Different numerical approaches to solving a Dirichlet or Neumann problem

\( \begin{align*} \text{Dirichlet} && \text{Neumann} \\ f''(x) &= 2x^2+5 \text{ on } (0, 1) & f''(x) &= 2x^2+5 \text{ on } (0, 1) \\ f(0) &= 1 & f'(0) &= 1 \\ f(1) &= 1 & f(1) &= 1 \\ f(x) &= \frac{1}{6} \left(x^4+15 x^2-16 x+6\right) & f(x) &= \frac{1}{6} \left(x^4+15 x^2+6 x-16\right) \end{align*} \)

were analysed. Theoretically, FDM and MLSM should match completely. This is practivaly demonstrated up to certain discretization level.

The interval \([0, 1]\) was always discretized uniformly using $N$ nodes, \(x_i = a+i h, h = (b-a)/N\).

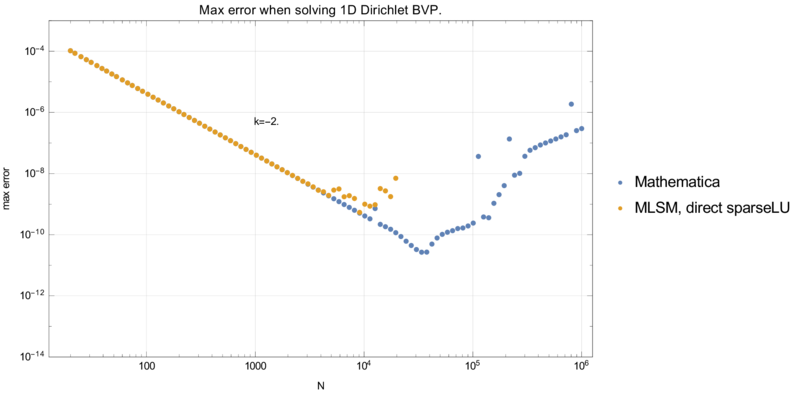
Dirichlet case

Precision and execution time are summarised in graphs below.

Neumann case

We have more that one possible disctretization of the Neumann BC in point 0. Three explored options are:

- onsided finite difference \(f'(0) \approx (f_1 - f_0) / h\) - symmetric finite difference \(f'(0) \approx (f_1 - f_{-1}) / h\) and normal discretization in node 0 \(f'(0) \approx (f_1 - 2f_0 + f_-1) /h^23\) - onsided double finite difference \(f'(0) \approx (-3/2 f_0 + 2f_1 - -1/2 f_2) / h\)