Analysis of MLSM performance

For starters, we can solve simple Diffusion equation $ \nabla^2 u = \frac{\partial u}{\partial t} $.

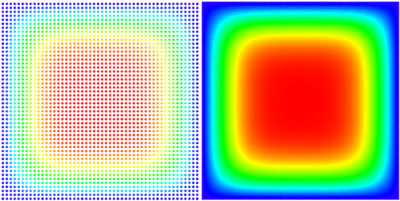
We solved the equation on a square $\Omega = [0, a] \times [0, a]$ with Dirichlet boundary conditions $ \left. u\right|_{\partial \Omega} = 0 $ and initial state $ u(t = 0) = 1$.

An analytical solution for this domain is known, and we use it to evaluate or own solution. \begin{equation} u(\vec{p}, t) = \sum_{\substack{n=1 \\ n \text{ odd}}}^\infty\sum_{\substack{m=1 \\ m \text{ odd}}}^\infty \frac{1}{\pi^2} \frac{16 a^2}{nm} \sin\left(\frac{\pi n}{a}p_x\right) \sin\left(\frac{\pi m}{a}p_y\right) e^{-\frac{\pi^2 (n^2+m^2)}{a^2}t} \end{equation} Because the solution is given in the series form, we only compare to the finite approximation, summing to $N = 100$ instead of infinity.

A picture of our solution (with smaller and larger node density):

Analysis of our method

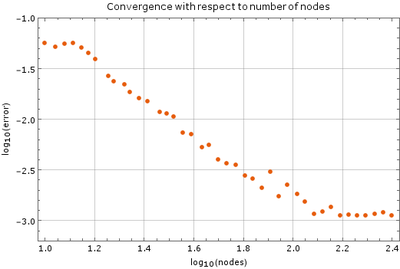
Convergence with respect to number of nodes

We tested the method with a fixed time step of $ \Delta t = 1\cdot 10^{-5}$ on a unit square ($a = 1$). Monomial basis of 6 monomials was used and 12 closest nodes counted as support for each node. After more than 250 nodes of discretization in each dimension the method diverges, which is expected. The stability criterion for diffusion equation in two dimensions is $\Delta t \leq \frac{1}{4} \Delta x^2$, where $\Delta x$ is the spatial discretization step in one dimension. In our case, at 250 nodes per side, the right hand side yields $\frac{1}{4}\cdot\frac{1}{250}\cdot\frac{1}{250} = 4\times 10^{-6}$, so our method is stable within the expected region.