Meshless FDM
Introduction
Consider Poisson equation in unit square with Dirichlet boundary conditions, i.e.
\begin{align*} \Delta u = f \; \text{in } \Omega = [0, 1]^2, \quad u = 0 \; \text{on } \partial \Omega. \end{align*}
Let $f(x,y) = -2\pi^2\sin(\pi x)\sin(\pi y)$, which gives the simple analytical solution $u(x,y) = \sin(\pi x)\sin(\pi y)$. We compare errors of:
- the known RBF-FD approach, and
- meshless FDM with 5-point and 9-point stencils (explained in detail below)
Meshless FDM
Ordinary FDM (finite difference method) uses a uniform grid for the domain – the spacing between the nodes is constant in each spatial direction –, and the derivative operators are (usually) approximated using central finite difference stencils. In the specific case of Poisson equation, we can discretize the 2D Laplace operator using the 5-point stencil which gives second-order accuracy, or the 9-point stencil which gives fourth-order accuracy (assuming that $u$ can be well approximated by a Taylor expansion). Given grid spacing $h$, the 5-point stencil is
\begin{align*} \Delta u(x, y) \approx \frac{1}{h^2} \cdot \bigl( - 4u(x,y) + u(x+h,y) + u(x,y+h) + u(x-h,y) + u(x, y-h) \bigr), \end{align*}
and the 9-point stencil is
\begin{align*} \Delta u(x, y) \approx \frac{1}{h^2} \cdot \Bigl( &- 5u(x,y) + \frac{4}{3} \cdot \left[ u(x+h,y) + u(x,y+h) + u(x-h,y) + u(x, y-h) \right] \\ &-\frac{1}{12} \cdot \left[ u(x+2h,y) + u(x,y+2h) + u(x-2h,y) + u(x, y-2h) \right] \Bigr). \end{align*}
A key point of this approach is that all of the nodes we use in the approximation are part of the grid.
Meshless methods do not assume a uniformly discretized domain and thus we cannot directly apply FDM. Taking a node $(x, y)$, it is unlikely that any of $(x+h,y), (x,y+h), \dots$ are in the discretization. Our approach to meshless FDM uses the usual FDM stencils by utilizing interpolation for the unknown grid nodes, as explained below.
Consider an arbitrary node $p = (x,y)$ from a meshless domain. To approximate a differential operator at this point, we first decide on the appropriate FDM stencil. Suppose that the stencil uses values in points $q_1, \dots, q_M$. For the 5-point stencil from before we have
\begin{align*} &q_1 = p, \; q_2 = p + (h, 0),\; q_3 = p + (0, h),\; q_4 = p + (-h, 0),\; q_5 = p + (0, -h), \\ &\Delta u(x, y) \approx \frac{1}{h^2} \cdot \bigl( - 4u(q_1) + u(q_2) + u(q_3) + u(q_4) + u(q_5) \bigr). \end{align*}
As these points[1] are not present in the domain, we perform RBF-FD interpolation for points $q_1, \dots, q_M$. The interpolation uses $n$ closest nodes to $p$, called the support of node $p$. With this, we can express $u(q_i)$ as a linear combination of $u(p_1), u(p_2), \dots, u(p_n)$, where $p_1, p_2, \dots, p_n$ are the support of $p$, and use the usual construction of the linear system for FDM.
To conclude, both the known RBF-FD approach and our meshless FDM approach work with nodes $p_i$ and values $u(p_i)$ at these nodes. We use the support of each node to either utilize the known approach or interpolate to FDM stencil nodes.
Domain generation
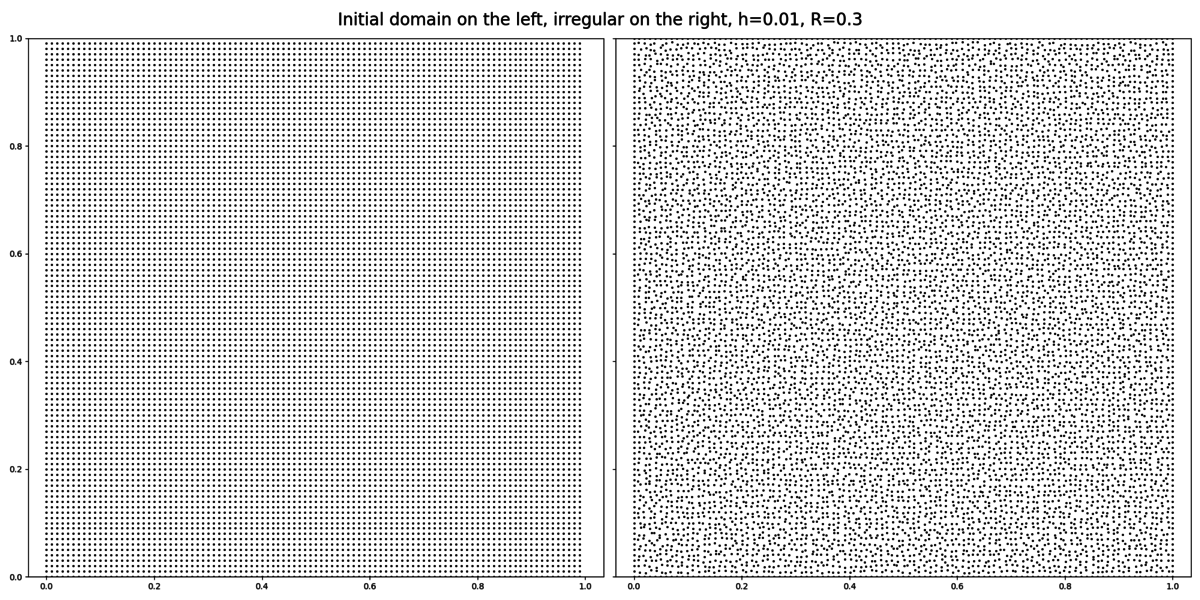
To obtain an irregular domain, we start with a unit square with a grid discretization of step $h$. We continue by creating a new domain, copying the boundary nodes, and repeating for each internal node $p_i = (x, y)$:
- Sample $a$ and $b$ from a uniform real distribution on $[-1, 1]$ (e.g. using a fixed seed for reproducability)
- Let $\tilde{x} = x + a \cdot Rh$ and $\tilde{y} = y + b \cdot Rh$ (where $R$ is an irregularization parameter)
- Add $\tilde{p_i} = (\tilde{x}, \tilde{y})$ as an interior node to the new domain
An example of this is shown in figure 1. Using parameter $R = 0.3$ results in a nicely irregularized domain, where nodes are visibly not aligned on a grid, while still having enough distance between each other.
Note: we could have used a fill algorithm to generate the domain.
Parameters
So far we mentioned parameters $h$ and $R$, which are used for domain generation.
Observe: using $h$ as the finite difference stencil step size might not be desirable – we wanted to test behavior for a variety of step sizes, and our $h$ is specific to our discretization process. From now on, let $\delta$ denote the step size for FDM stencils. In a general case, we would need to somehow decide on a value for $\delta$. Note that this could be per-node (e.g. calculate $\delta$ from the support) or a global value (e.g. calculate some statistic of the discretization).
We defined globally $\delta = \sigma \cdot h$ and conducted testing for various values of $\sigma > 0$, although stopping at not much more than $1$.
We used the same approximation engine for both the RBF-FD approach and the meshless FDM approach, namely a RBFFD engine with polyharmonic radial basis functions of order $3$ and monomial augmentation of order $m \in \{2, 4, 6\}$. Both methods used the same set of support nodes, however, in the FDM approach we used two interpolation techniques:
- "Simple": use the support nodes of the central node in the stencil for all of the nodes in the stencil (the approach used in the results section unless mentioned otherwise)
- "Advanced": find the support (closest $n$ nodes) for each node from the stencil separately (computationally more expensive).
Note: we chose support size in line with guidelines from the paper "Monomial augmentation guidelines for RBF-FD from accuracy vs. computational time perspective" (Mitja Jančič, Jure Slak, Gregor Kosec – 2021). Using lower support sizes yielded worse results.
Results
We compared the relative error of both approaches w.r.t. the analytical solution. Using different values of $\sigma$ we found that the error is lowest either near $\sigma \approx 1$ either near $\sigma \approx 0$. The $\sigma$ parameter affects only the meshless FDM approach.
We started with the 5-point stencil. With second order monomials, the meshless FDM approach gives better results than RBF-FD, especially in the region around $\sigma \approx 1$. Using higher-order monomials without increasing the FDM stencil size results in worse behavior compared to RBF-RD, although the results are still better than for $m=2$. We think that the higher error when using $m=4$ or larger comes from the fact that the 5-point stencil has an error proportional to the fourth derivative $u^{(4)} \cdot h^2$, and using $m=4$ or larger introduces this error. We see that the error matches RBF-FD at very low $\sigma$ values, but we incur great numerical errors by lowering it further and further to zero, as can be seen in figure 2.
Continuing with the 9-point stencil in figure 3, we see a considerable improvement. The meshless FDM method works better than RBF-FD even for fourth order monomials, also around $\sigma \approx 1$. Increasing monomial augmentation to sixth order or higher has a similar effect as before. This tells us that if we want to perform better than the known RBF-FD approach we need to properly match the FDM stencil size and the order of monomial augmentation.
Both interpolation techniques perform similarly well. We tried this for both the 5-point and the 9-point FDM stencil, see figure 4. For the 5-point stencil, the minimum of the error is slightly lower using the advanced technique, while the opposite holds for the 9-point stencil.
Increasing $\sigma$ much more than $1$ causes the error to grow quickly as evident in figure 5. Interestingly, the maximum of the error keeps decreasing for a while. Starting around $\sigma \approx 1.9$ the computation takes much longer as the linear system solver reaches the maximum number of iterations.
- ↑ Apart from the central point of the stencil, $q_1$