Scattering from an infinite cylinder

Back to Computational electromagnetics.

Case

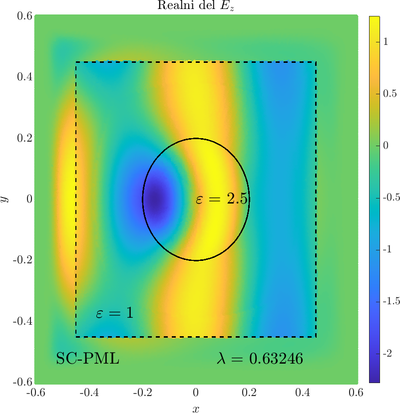
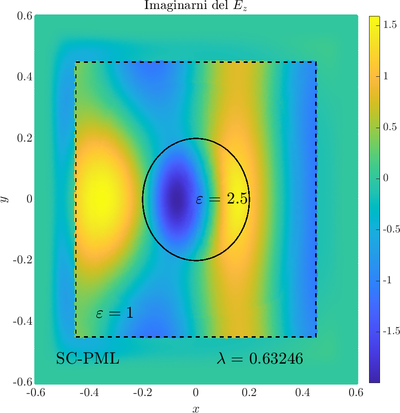
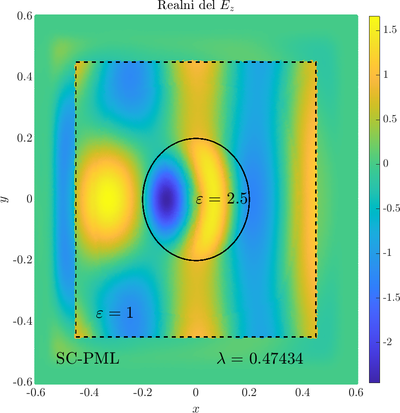
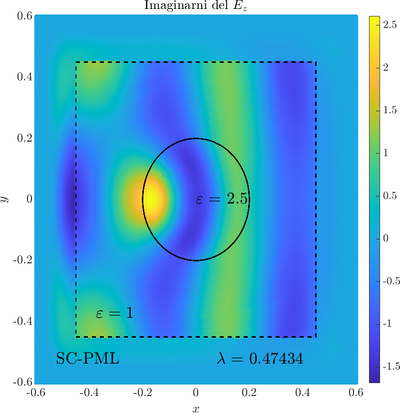
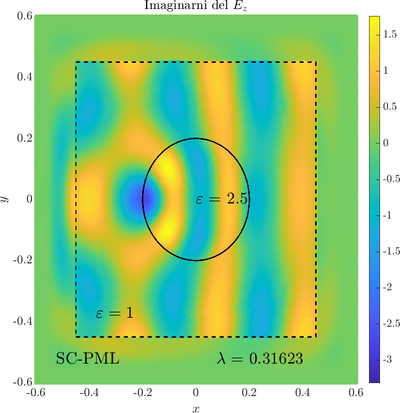
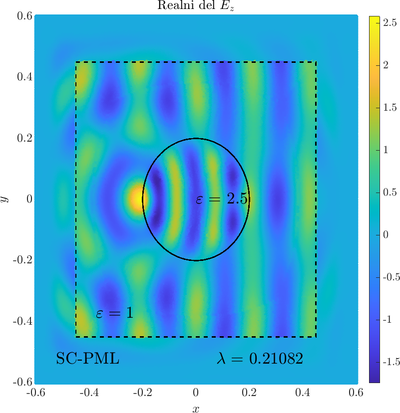
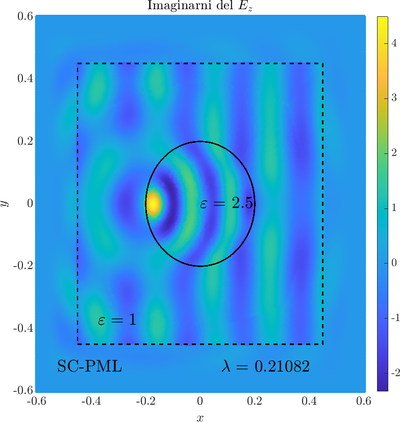
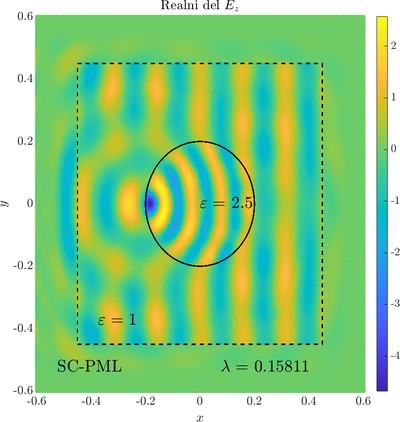
\( \newcommand{\eps}{\varepsilon} \newcommand{\dpar}[2]{\frac{\partial #1}{\partial #2}} \newcommand{\ddpar}[2]{\frac{\partial^2 #1}{\partial #2^2}} \def\doubleunderline#1{\underline{\underline{#1}}}\) As a simple two dimensional case let us consider a plane wave scattering on a dielectric cylinder. This case is important for two reasons, firstly, it shows how to encode the incident wave into the boundary between the cylinder and free space and thus calculate only with the scattered field outside. It shows how to use analytic expressions to represent sources with known analytical solutions, this is especially useful when dealing with point sources. Zgled je pomemben iz dveh razlogov, prvi\v c, ogledali si bomo kako vpadno polje zapi\v semo v rob med materialom in prostim prostorom in lahko kot take vire analiti\v cno predstavimo\footnote{Tu to ne pride posebno prav, ker imamo opravka z ravnim valom, v primerih ko imamo to\v ckaste izvire pa je zelo prakti\v cno.}. Secondly the problem has a relatively simple analytical solution in terms of Hankel funitons and can be used as a benchmark case.The problem is defined in two domains, inside and outside the cylinder, we are solving the following system of two PDE that are coupled on the inside boundary \begin{align} \nabla^2 v +\eps_r \frac{\omega^2}{c_0^2}\thinspace v = 0 \qquad &\text{and} \quad \Omega \label{eq:inner} \\ \nabla^2 u^s + \frac{\omega^2}{c_0^2}u^s = 0 \qquad & \text{outside} \quad \Omega \label{eq:outer} \end{align} The field $v$ is the total field inside, $u^s$ is only the scattered part of $E_z$ Outside the cylinder. The boundary conditions are \begin{equation} v - u^s =u^i \qquad \text{on} \quad \partial \Omega \label{eq:BC1}, \qquad \text{and} \qquad \dpar{v}{n} - \frac{1}{\eps_r}\dpar{u^s}{n} = \dpar{u^i}{n} \qquad \text{on} \quad \partial \Omega. \end{equation} The incident field $u^i$ has an analytical form in our case a plane wave $e^{ikx}$, since it has a nice closed form we know its derivatives and the boundary conditions are nicely expressed. Around the computational domain we use a PML to simulate an infinite domain.

Results