Computational electromagnetics

Case studies

The following pages describe the basics of computational electromagnetics, starting with relevant derivations and the basics of classical electromagnetism. The subpages include case studies with analytical solutions if they exist and numerical solutions.

• Triple dielectric step in 1D
• Photonic crystal in 1D
• Scattering from an infinite cylinder
• Point source near an anisotropic lens

Classical electromagnetism

Maxwell's equations in matter

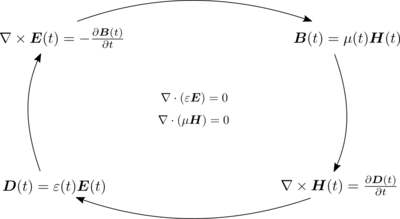
Classical electrodynamics is historically one of the most eminent fields of physics as an extension of classical mechanics, it is very successful in explaining a plethora of phenomena. The dynamics of electric and magnetic fields are described with Maxwell's equations. As we will be studying the interaction of electromagnetic waves with different objects, we need Maxwell's equations in matter \( \newcommand{\dpar}[2]{\frac{\partial #1}{\partial #2}} \begin{align} &\nabla \times \b{E}(\b{r}, t) = - \dpar{\b{B}(\b{r}, t)}{t}, \label{eq:TFaraday} \\ &\nabla \times \b{H}(\b{r}, t) = \b{j}(\b{r}, t) + \dpar{\b{D}(\b{r}, t)}{t}, \label{eq:TMaxwell-Ampere} \\ &\nabla \cdot \b{D}(\b{r}, t) = \rho(\b{r}, t), \label{eq:TGaussE} \\ &\nabla \cdot \b{B}(\b{r}, t) = 0. \label{eq:TGaussM} \end{align} \)

The system of equations contains four fields. The electric field strength $\b E$ and density $\b D$ and the magnetic field strength $\b H$ and density $\b B$. The four fields are accompanied by the current density $\b j$ and the charge density $\rho$. For a full description of electromagnetic phenomena, we need to provide another two constitutive equations, that relate the strength and density of the fields \( \newcommand{\eps}{\varepsilon} \begin{align} \b{B} &= \mu_0 \mu \b{H}, \label{eq:constM} \\ \b{D} &= \eps_0 \eps \b{E} \label{eq:constE} \end{align} \) where $\varepsilon_0$ and $\mu_0$ are vacuum permittivity and permeability respectively. The dielectric function $\varepsilon$ and magnetic permeability $\mu$ are in general dependant on both $\b E$ and $\b B$ as well as the frequency $\omega$ and can be second order tensors in anisotropic materials. Equations \eqref{eq:constM} and \eqref{eq:constE} already assume linear material properties, generally the polarisation $\b P$ and magnetisation are defined as power series expansions of the electric field density and magnetic field density, as \( \begin{align} \label{eq:PMexpans} \b{P} &= \chi_E \b{D} + \mathcal{O}(D^2), \\ \b{M} &= \chi_M \b{H} + \mathcal{O}(H^2). \end{align} \) The material linearity assumption holds well for small external fields, meaning small $\b D$ and $\b H$. The treatment of nonlinear terms falls within the field of nonlinear optics and is not relevant for our discussion here.

Electromagnetic waves

\( \def\doubleunderline#1{\underline{\underline{#1}}} \newcommand{\dpar}[2]{\frac{\partial #1}{\partial #2}} \newcommand{\ddpar}[2]{\frac{\partial^2 #1}{\partial #2^2}} \newcommand{\eps}{\varepsilon} \) When studying light and related phenomena, we are usually interested in the behavior of electromagnetic waves, where the electric and magnetic fields oscillate with constant frequency and propagate in a single direction. The wave formulation helps with understanding optical phenomena such as diffraction and reflection and offers easily graspable quantities such as wave amplitude and wavelength. Wave equations for $\b E$ and $\b H$ can be derived from Maxwell's equations for linear and homogeneous materials. Let's start by treating a more general case, where $\doubleunderline \varepsilon$ is a constant second-order tensor and $\mu$ is a scalar quantity. From Maxwell's equations and constitutive relations we obtain \begin{equation} \nabla \times \left[ \doubleunderline{\varepsilon}^{-1} \nabla \times \b{H} \right] = \nabla \times \left[ \doubleunderline{\varepsilon}^{-1} \b j \right] - \mu \mu_0 \varepsilon_0 \ddpar{\b H}{t}. \end{equation} and \begin{equation} \nabla \times \nabla \times \b{E} = \nabla (\nabla \cdot \b E) - \nabla^2 \b E = -\mu\mu_0\dpar{\b j}{t} - \eps_0 \doubleunderline{\varepsilon} \mu \mu_0 \ddpar{\b E}{t} \end{equation} which simplify to wave equations for homogenous (linear) materials and no external currents and charges \begin{equation} \nabla^2 \b E = \eps\eps_0\mu\mu_0\ddpar{\b E}{t}, \qquad \text{ or } \qquad \nabla^2 \b H = \eps\eps_0\mu\mu_0\ddpar{\b H}{t}. \end{equation} One possible way of solving electromagnetic problems is simply to solve the above wave equations numerically. Another approach is to solve Maxwell's equations in the frequency domain. We start by Fourier expansion of the fields $\b E$, $\b D$, $\b B$ and $\b H$ analogous to \begin{equation} \label{eq:Fdecomp} \b{E}(\b{r}, t) = \int\frac{d\omega}{2\pi} \b{E}(\b{r}, \omega) e^{-i\omega t}, \end{equation} in the frequency domainall the fields become complex. The ratio between the real and complex component of the fields is the phase difference of the material response to external fields. The Fourier expansion leads to the harmonic form of Maxwell's equations \begin{equation} \label{eq:FFaraday} \nabla \times \b{E}(\b{r}, \omega) = - i\omega \b{B} (\b{r}, \omega), \end{equation} \begin{equation} \label{eq:FMaxwell-Ampere} \nabla \times \b{H}(\b{r}, \omega) = i\omega \b{D}(\b{r}, \omega). \end{equation} The constitutive relations are unchanged. If we assume that there are currents we obtain a wave equation for either $\b D$ or $\b H$, \begin{equation} \label{eq:frekaniwave} \nabla \times \left[ \doubleunderline{\eps}^{-1} \nabla \times \b{H} \right] = \omega^2 \mu_0 \eps_0 \mu \b{H}. \end{equation} The above form allows for a calculation of a steady state response to an incident harmonic plane wave, meaning that we can study scattering of any incident wave that can be represented by a plane wave expansion. The time dependent solution is obtained by an inverse Fourier transform. In empty space \eqref{eq:frekaniwave} simplifies to the Helmholtz equation \begin{equation} \label{eq:frekemptywave} \nabla^2 \b{H} = - \omega^2 \mu_0 \eps_0 \b{H} = - k^2 \b{H}. \end{equation} Wavenumber $k$ in a vacuum is defined as $k = \omega \sqrt{\mu_0 \epsilon_0} = \frac{2 \pi}{\lambda}$. One of the major advantages of the frequency domain approach over the time domain approach is that the frequency dependence of the dielectric function does not need to be considered, as one simply uses the value of the dielectric function at a certain frequency.

Boundary conditions for Maxwell's equations

For modeling purposes the treatment of electromagnetic fields on boundaries between materials with different properties, such as $\varepsilon$ and $\mu$, is crucial. The boundary conditions for Maxwell's equations between two linear and homogenous mediums are as follows \begin{equation} \begin{array}{rl} D_{1 n}-D_{2 n}=\sigma, \qquad & E_{1 t}-E_{2 t}=0 \\ B_{1 n}-B_{2 n}=0, \qquad & H_{1 t}-H_{2 t}=K.\end{array} \end{equation} Where we have fields $\b{E}_1, \b{D}_1, \b{B}_1, \b{H}_1$ in medium $1$ and fields $\b{E}_2, \b{D}_2, \b{B}_2, \b{H}_2$ in medium $2$. Subscript $t$ and $n$ denote the tangential and normal component respectively, $\sigma$ is the surface charge density and $\b K$ is the surface current density.

Frequency dependence of the dielectric function

As mentioned above the dielectric function $\varepsilon$ is a function of frequency. Some analytical properties of the dielectric function $\varepsilon(\omega)$ are well known, due to their relevance in optics, one example being the Kramers-Kronig relations. The dielectric function is in general, based on a nonlocal response function $\chi$, defined as \begin{equation} \varepsilon(\omega) = 1 + \int_{0}^{\infty} \chi(\tau) e^{i \omega \tau} \text{d}\tau. \end{equation} For a more detailed analysis of the analytical properties of the function, refer to any standard optics or advanced electromagnetics textbook. When it comes to numerical simulations, models of the dielectric function are of more interest than its analytical properties.

Dielectric materials

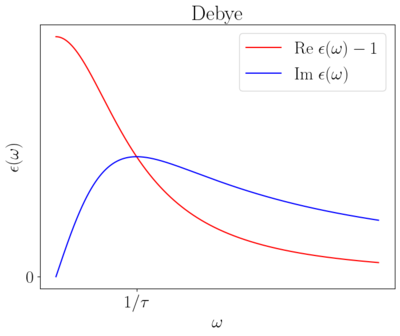
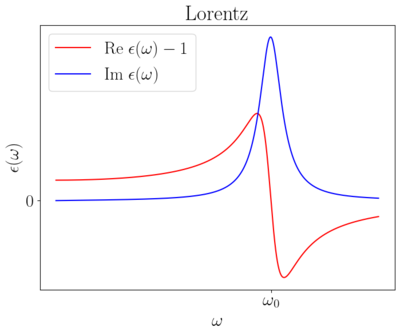
The simplest model for dielectrics is based on the equation of motion for the bound charges \begin{equation} m \frac{\mathrm{d}^{2} \mathbf{r}}{\mathrm{d} t^{2}}=-m \gamma \dot{\mathbf{r}}-m \omega_{0}^{2} \mathbf{r}+e \mathbf{E}(t) \end{equation} the terms on the right side describe the dissipation of energy, oscillations and the driving force of the external electric field. A short calculation leads to an expression of the frequency dependence of the dielectric function \begin{equation} \varepsilon(\omega)=1+ \frac{\omega_p}{\left(\omega_{0}^{2}-\omega^{2}\right)-i \gamma \omega}. \end{equation} The above expression can be simplified for high and low frequencies leading to the so-called Debye and Plasmonic relaxation models. The Lorentz model applies for frequencies where no terms in the denominator can be neglected. Typical Debye and Lorentz relaxations are shown in the plots below.

In general, the dielectric function of a material is modeled as a sum of many Debye and Lorentz relaxations, the parameters of which are determined by microscopic properties of the material itself, an extremely interesting case study is the dielectric function of water.

Conductors

When dealing with conductors we use the Drude model of conduction \begin{equation} m \frac{d \mathbf{v}(t)}{d t}=-m \gamma \mathbf{v}(t)+e \mathbf{E}(t) \end{equation} from which we quickly derive the equation for conductivity \begin{equation} \sigma(\omega)=\frac{n e^{2}}{m} \frac{1}{\gamma-i \omega}, \end{equation} which we can relate to the dielectric function \begin{equation} \varepsilon(\omega)=1-\frac{\sigma(\omega)}{i \varepsilon_{0} \omega}. \end{equation}

Modeling in the time domain

The single most frequent type of calculation used in computational electromagnetics is the simulation of electromagnetic fields in the time domain. The calculation propagates $\b E(\b r, t)$ and $\b H(\b r, t)$ in time, usually starting with all fields set to zero and some time dependent current source $\b J(\b r, t)$. The main advantage of time domain approaches is the ability to study transient phenomena while its main drawback is the study resonant problems.

Finite differences in time domain (FDTD)

Formulation

Finite differences in time domain were suggested in 1966 by Yee. The method uses finite differences to discretize Maxwell's equations and propagates the fields in time by alternating between updating the electric field strength and magnetic field strength. One of its defining attributes is the use of a staggered grid to represent $\b H$ and $\b E$ nodes. The staggered grid simplifies the calculation of curl expressions and helps with numerical stability and treating the boundaries of materials.

This type of solution procedure provides an alternative to solving the wave equation for either $\b H$ or $\b E$.

Modeling sources

Since we are starting with all fields set to zero, we need to somehow introduce power into the model. This is usually done with current sources. The current signal used depends on the type of calculation. If we are interested in a steady-state solution we would use a sinusoidal source, that is slowly turned on and simulated the device until a steady state is reached. On the other hand, if we are interested in calculating the response of a device to many frequencies, we would use a Gaussian pulse and simulate the device until all the energy has left the system.

Taflove in his book [1] differentiates between five types of sources. The easiest to implement are so-called hard sources, where one simply sets the value of a field in a node to the source value e.g. \begin{equation} \b E_z(i, t) = \sin 2\pi ft. \end{equation} The problem is that the node now acts as a perfect dielectric and incoming waves reflect from the point and do not pass through as they should. On the other hand one can use a soft source where energy is inserted into the domain via electric and magnetic (non-physical) current \begin{equation} \b E_z(i, t) = E_z(i, t) + J(t) \qquad \text{in} \qquad \b H_x(i, t) = H_x(i, t) + M(t). \end{equation} Waves no longer reflect from the source, however, the source still radiates in all directions, which is sometimes not desired. This issue is solved with TFSF (total field, scattered field) sources, which are based on the linearity of Maxwell's equations and allow to construct sources that inject the energy only in the desired direction. This is accomplished by decomposing the total fields into the scattered and incident \begin{equation} \b{E} = \b{E}^i + \b{E}^s \text{, } \qquad \b{H} = \b{H}^i + \b{H}^s. \end{equation} and then dividing the computational domain $\Omega$ into two subdomains. In one of the subdomains, we calculate only using the scattered part of the fields and in the other, we calculate with the total field. With careful treatment of the boundary between the subdomains one can construct an arbitrary incident wave. Alongside the already mentioned source types, waveguide sources and total scattered field sources. For an in-depth discussion refer to Taflove [1].

Transmittance and Reflectivity

Transmittance and reflectivity are dependent on the frequency of the incoming wave. One of the main strengths of time domain calculations is that one can calculate both coefficients for a wide frequency range with a single simulation. This is achieved by using a source that contains a wide range of frequencies i.e. a short Gaussian pulse.

Let us illustrate how to calculate $R$ and $T$ in one dimension. The calculation is similar in higher dimensions. We make two assumptions, firstly the source is directed directly into the device. This means that we will have only the reflected field on one side of the device and only the transmitted field on the other side of the device. Secondly, we assume that nothing reflects from the edges of the domain. We record the signals on both edges of the domain and label them $E_r(t)$ for reflected and $E_t(t)$ for transmitted. It is important to simulate for a long enough time that there is no energy left in the device. Otherwise, the calculation of the coefficients has not converged yet. The Fourier transforms of the signals at the edges, along with the transform of the source, define $R$ and $T$ \begin{equation} R(\omega) = \left| \frac{E_o(\omega)}{S(\omega)} \right| \qquad \text{and} \qquad T(\omega)= \left| \frac{E_p(\omega)}{S(\omega)} \right|. \end{equation} Since we only know the field values at discrete time intervals the transformation is discrete \begin{equation} F(\omega) \cong \Delta t \sum_{m=1}^{M}\left(e^{-j \omega \Delta t}\right)^{m} \cdot f(m \Delta t), \end{equation} in practice, so that it is not needed to store the signals on both edges which may take up considerable computer memory, the sum can be calculated after each step in the simulation to save space.

\( \newcommand{\eps}{\varepsilon} \newcommand{\dpar}[2]{\frac{\partial #1}{\partial #2}} \newcommand{\ddpar}[2]{\frac{\partial^2 #1}{\partial #2^2}} \def\doubleunderline#1{\underline{\underline{#1}}} \)

Modeling in the frequency domain

In the frequency domain, two types of calculations are most common. Within the field of photonic crystals, bandstructures of periodic materials are sought by solving a generalized eigenvalue problem $Ax = \omega^2Bx$. In engineering applications, a response of a structure to a periodical source $\b J(x) e^{-i\omega t}$ is more often calculated. We will focus on the second type of calculation.

Formulation

We need to solve the equation that can be derived by combining Maxwell's equations and constitutive relations \begin{equation} \left[(\nabla \times \nabla \times)-\frac{\omega^{2}}{c^{2}} \varepsilon(\mathbf{r})\right] \mathbf{E}(\mathbf{r})=i \omega \mu_{0} \mathbf{J}(\mathbf{r}). \end{equation} The electric field strength $\b E(\b r)$ is complex, the time dependent solution is obtained via $\b E(\b r,t) = \b E(\b r) e^{i\omega t}$. The magnetic field can be obtained by taking a curl of the solution above \begin{equation} \mathbf{H}=-\frac{i}{\omega \mu_{0}} \nabla \times \mathbf{E}. \end{equation}

Absorbing boundary conditions

Absorbing boundary conditions in the frequency domain can be realized in a number of ways. One of the most straight forward approaches is to impose the Sommerfeld radiation condition or a numerical approximation of it. However, it is more common to surround the computational domain with a thin absorbing layer, which does not reflect outgoing waves. The perfectly matched layer (PML) is one of such absorbing boundary conditions. There are many variants of PML's, but it is clear that the use of one worsens the conditioning of the problem matrix [2]. As it turns out UPML (Uniaxial PML) is numerically less stable than SC-PML (stretched coordinate PML), but efficient preconditioners exist for cases when SC-PML is hard to implement.

Uniaxial Perfectly Matched Layer

Inside the computational domain we have an amplitude equation for $\b E$, \begin{equation} \nabla \times \doubleunderline{\mu}^{-1} \nabla \times \mathbf{E}-\omega^{2} \varepsilon \mathbf{E}=-\mathrm{i} \omega \mathbf{J}. \end{equation} We surround the computational domain $\Omega$ with a thin domain $\Omega'$, where we have an uniaxial anisotropic material, which damps the electromagnetic field \begin{equation} \nabla \times \doubleunderline{\mu_{s}}^{-1} \nabla \times \mathbf{E}-\omega^{2} \doubleunderline{\varepsilon_{s}} \mathbf{E}=-\mathrm{i} \omega \mathbf{J} \end{equation} dielectric and permeability tensors are diagonal, \begin{equation} \doubleunderline{\varepsilon_{s}}=\varepsilon\left[\begin{array}{ccc}\frac{s_{y} s_{z}}{s_{x}} & 0 & 0 \\ 0 & \frac{s_{s} s_{x}}{s_{y}} & 0 \\ 0 & 0 & \frac{s_{x} s_{y}}{s_{z}}\end{array}\right], \quad \doubleunderline{\mu_{s}}=\mu\left[\begin{array}{ccc}\frac{s_{y} s_{z}}{s_{x}} & 0 & 0 \\ 0 & \frac{s_{z} s_{x}}{s_{y}} & 0 \\ 0 & 0 & \frac{s_{x} s_{y}}{s_{z}}\end{array}\right]. \end{equation} To avoid reflections of waves from the boundary between layers, we slowly turn on the loss parameter $s_w$ \begin{equation} s_{w}(l)=1-\mathrm{i} \frac{\sigma_{w}(l)}{\omega \varepsilon_{0}} \end{equation} where $l$ is the distance from the boundary of the PML.

Streched Coordinate Perfectly Matched Layer

In the stretched coordinate PML the coordinates are stretched and the PML no longer resembles any physical material. The equation inside the PML remains unchanged, \begin{equation} \label{eq:SC-PML} \nabla_{s} \times \mu^{-1} \nabla_{s} \times \mathbf{E}-\omega^{2} \varepsilon \mathbf{E}=-\mathrm{i} \omega \mathbf{J}. \end{equation} However, the gradient is redefined as \begin{equation} \nabla_{s}=\hat{e}_x \frac{1}{s_{x}} \frac{\partial}{\partial x}+\hat{e}_y \frac{1}{s_{y}} \frac{\partial}{\partial y}+\hat{e}_z \frac{1}{s_{z}} \frac{\partial}{\partial z}. \end{equation} Just like with UPML, the damping is slowly turned on. SC-PML is considered more stable than UMPL, but it is usually trickier to implement. For a magnetically homogenous and isotropic medium the SC-PML equation simplifies to \begin{equation} -\nabla^2_s\b E + \nabla_s\left( \nabla_{s} \cdot \b E \right) -\omega^2 \eps \mu \b E = -i\omega\b J, \end{equation} in matrix form \begin{multline} - \begin{bmatrix} \frac{1}{s_x} \frac{\partial}{\partial x} \left(\frac{1}{s_x}\dpar{E_x}{x}\right) + \frac{1}{s_y} \frac{\partial}{\partial y} \left(\frac{1}{s_y}\dpar{E_x}{y}\right) + \frac{1}{s_z} \frac{\partial}{\partial z} \left(\frac{1}{s_z}\dpar{E_x}{z}\right) \\ \frac{1}{s_x} \frac{\partial}{\partial x} \left(\frac{1}{s_x}\dpar{E_y}{x}\right) + \frac{1}{s_y} \frac{\partial}{\partial y} \left(\frac{1}{s_y}\dpar{E_y}{y}\right) + \frac{1}{s_z} \frac{\partial}{\partial z} \left(\frac{1}{s_z}\dpar{E_y}{z}\right) \\ \frac{1}{s_x} \frac{\partial}{\partial x} \left(\frac{1}{s_x}\dpar{E_z}{x}\right) + \frac{1}{s_y} \frac{\partial}{\partial y} \left(\frac{1}{s_y}\dpar{E_z}{y}\right) + \frac{1}{s_z} \frac{\partial}{\partial z} \left(\frac{1}{s_z}\dpar{E_z}{z}\right) \end{bmatrix} + \begin{bmatrix} \frac{1}{s_x} \frac{\partial}{\partial x} \left(\frac{1}{s_x}\dpar{E_x}{x}\right) + \frac{1}{s_y s_x}\frac{\partial E_y}{\partial x \partial y} + \frac{1}{s_z s_x}\frac{\partial E_z}{\partial z \partial z} \\ \frac{1}{s_x s_y}\frac{\partial E_x}{\partial y \partial x} + \frac{1}{s_y} \frac{\partial}{\partial y} \left(\frac{1}{s_y}\dpar{E_y}{y}\right) + \frac{1}{s_z s_y}\frac{\partial E_z}{\partial y \partial z} \\ \frac{1}{s_x s_z}\frac{\partial E_x}{\partial z \partial x} + \frac{1}{s_y s_z}\frac{\partial E_y}{\partial z \partial y} + \frac{1}{s_z} \frac{\partial}{\partial z} \left(\frac{1}{s_z}\dpar{E_z}{z}\right) \end{bmatrix} - \\ -\omega^2 \eps \mu \b E \begin{bmatrix} E_x \\ E_y \\ E_z \end{bmatrix} = -i\omega \begin{bmatrix} J_x \\ J_y \\ J_z \end{bmatrix} \end{multline} The expression further simplifies in cases where some of $s_w$'s are constant (cartesian coordinates).

Benchmarking

Parameters of the PML are usually determined empirically, separately for each simulation, however, there are some rules of thumb. PMLs by Berenger's definition are exact for a continuous equation. When the equation is discretized reflections appear at the boundary of the PML. A lot of care needs to be taken so that the reflections are minimized. This is usually achieved by giving $\sigma_{w}(l)$ a polynomial relationship with the distance $l$ from the PML boundary \begin{equation} \sigma_{w}(l,) = \sigma_{max}\left(\frac{l}{d}\right)^m \end{equation}

where $\sigma_{max}$ is the maximum loss parameter, $d$ is the thickness of the layer and $m$ is the power of the polynomial, and usually lies somewhere between $2$ and $4$. For a normally incident wave on the PML, we can choose the Reflectance of the PML and accordingly tune parameters $d$ and $m$ via \begin{equation} \sigma_{w, \max }=-\frac{(m+1) \ln R}{2 \eta_{0} d} \end{equation} where $\eta_0$ is the Impedance of free space.