Heat equation

Go back to Examples.

This example shows how explicit method of solving partial differential equations is used within the Medusa library. Firstly, this example compares explicit solutions to analytical, then it shows how it can be used to solve heat transfer equation.

Domain

In this example, a square domain with a cut-out hole in the middle is used. The hole has radius equal to 1/3 of length of a square. Domain nodes are placed randomly with about dx length distance between them. Domain boundary is separated in to 5 areas: up, down, left, right and center. The idea is to have Dirichlet boundary condition on the square (up, down, left and right) and Neumann boundary conditions in the middle (center).

Fuction

The function used for this example is $u(x,y) = \sin(\pi x)\sin(\pi y)$. Laplace operator of this function is $\Delta u(x,y)=-2\pi^2\sin(\pi x)\sin(\pi y)$. For comparing explicit solution to analytical, we solve function for each node and save solution to $u\_analytic$. With this we also calculate Dirichlet boundary conditions. Then we set domain interior and nodes with Neumann bondary conditions to arbitrary value, in this case 0. We proceed to explicitly solve the domain. In the domain interior we are solving the following equation\[ \begin{align*} u (x,y,t+1) = dt*\bigg(\Delta u(x,y,t) + 2\pi^2\sin(\pi x)\sin(\pi y)\bigg)+u(x,y,t) \end{align*} \]

For Neumann bondary conditions we set $u(x,y,t+1)$ in a way that it satisfies the following equation\[ \frac{\partial u(x,y,t+1)}{\partial n}=n_x \pi \cos(\pi x) \sin(\pi y)+n_y \pi \sin(\pi x) \cos(\pi y) \]

After the simulation is finished, we can easily calculate relative error. Values of nodes are saved in a vector $u1$, so we can use norm of $|u1 - u\_analytic|$ to calculate error, then divide it by norm of $u1$ to calculate relative error.

\( \begin{align*} relative\_error = \frac{\sqrt{\sum{|u1-u\_analytic|^2}}}{\sqrt{\sum{|u1|^2}}} \end{align*} \)

Weighted Least Squares (WLS)

In this simulation, we use Gaussians for our WLS. Because of scattred nodes in our domain, we have to use 9 basis. The support size we chose is 27. For weight we have chosen 1.0 and for Gaussian weight (sigma) 75. Later we will look how change of sigma and weight effects relative error.

1 WLS<Gaussians<Vec2d>, GaussianWeight<Vec2d>, ScaleToClosest> wls({9, 75.0}, 1.0);

Finding steady state

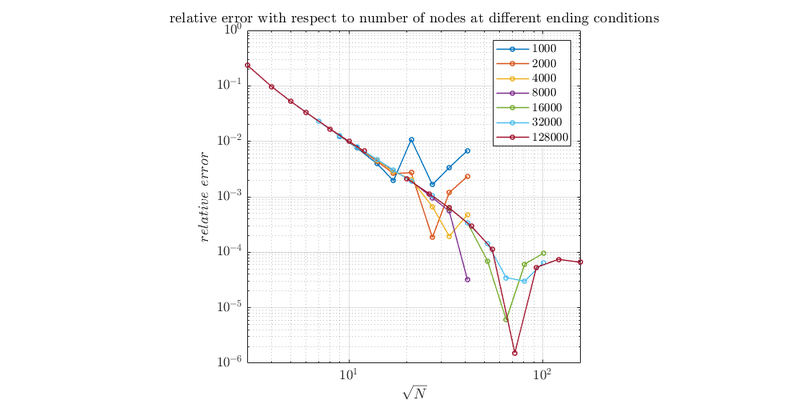
To finish simulation we save values of nodes and compare them after some time steps. Next graph shows us how relative error changes, when we increase number of steps, after which we compare values.

In this graph we can see, that using 8000 time steps is sufficient for the size of our domain, which we will use in further simulations.

Effect of sigma and weight

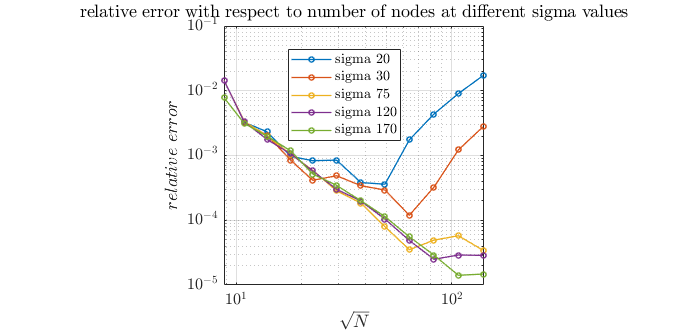
To see the effect of sigma, we ran the same simulation twice and got following graphs:

(Graphs aren't identical. This is probably due to a slightly different domain. This happens becouse domain is generated with a bit of randomness.)?

We can see is that value of sigma has a big effect on relative error.

Go back to Examples.