Convection Diffusion equation

Before moving to more complex numerical examples, preliminary tests are done on a case with a known closed form solution. As in all the previous examples, we use the diffusion equation for a test case. The main purpose of this section is basic evaluation of mesh based against meshless methods, as well as strong form against weak form methods.

A 2D diffusion equation in its dimensionless form is considered: \begin{align} %??? brezdimenzijska oblika nima c \frac{\partial u}{\partial t} - \alpha \nabla^2u = q, & \qquad (x, y)\in \Omega, \label{eq.diffu}\\ % \frac{\partial u(x,y,t)}{\partial t} = \nabla^2 u(x,y,t), & \qquad (x, y)\in \Omega, \label{eq.diffusion}\\ u(x,y,t) = \overline{u}(x,y,t), & \qquad (x,y) \in \Gamma_D,\label{eq.bc_diffu}\\ u(x,y,t),_n = \overline{g}(x,y,t), & \qquad (x,y) \in \Gamma_N, \label{eq.mixed.bc_diffu}\\ u(x,y,t) = u_0, & \qquad t=0,\label{eq.ic_diffu} \end{align} where $(x,y)$ are spatial coordinates, $t$ is time, $u(x, y, t)$ is the unknown solution, $ \Omega$, and $ \Gamma_D$ and $ \Gamma_N$ are the global domain with Dirichlet boundary and Neumann boundary, $\overline{u}$ and $\overline{g}$ are the prescribed Dirichlet and Neumann boundary values and $u(x,y,0)=u_0$ is the known initial condition.

In following discussion we present some solutions and test we did while coding our library. Please refer to our repository for full set of latest examples and tests

Steady state 1D case

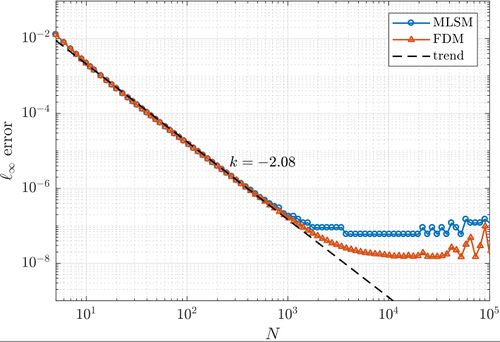
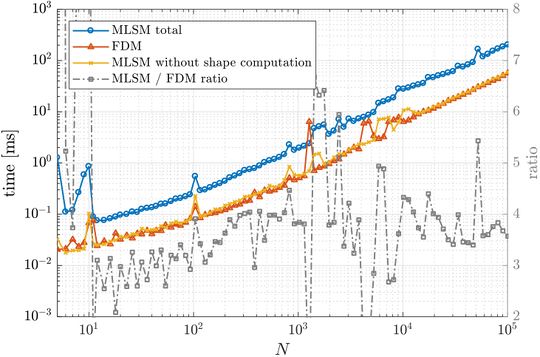
First, a simple one dimensional case is tackled to assess basic properties of presented solution method. Consider the problem \begin{align} u''(x) &= \sin(x), \quad x \in (0, 1) \nonumber \\ u(0) &= 0 \label{eq:neu1d} \\ u'(1) &= 0 \nonumber \end{align} with analytical solution \begin{equation} u(x) = x \cos 1 - \sin x. \end{equation} We solve the problem with MLSM using 3 support nodes and 3 monomials $\{1, x, x^2\}$ as basis functions on a regularly distributed nodes. This setup of MLSM is theoretically equivalent to the Finite Difference Method (FDM) and therefore it is worth implementing also standard FDM to compare results and execution times. The error between the actual solution $u$ and the approximate solution $\hat{u}$ is measured in $\ell_\infty$ norm, \begin{equation} \|u - \hat{u}\|_{\ell_\infty} = \max_{x\in X} | u(x) - \hat{u}(x)|, \label{eq:linf-err} \end{equation} where $X$ is the set of all points in the domain. The problem can be solved with below code. Note, that the code is the same for 1,2 and 3D cases

1 for (int i : domain.internal()) {
2     op.lap(M, i, 1.0);  // Equation.
3     rhs(i) = std::sin(domain.positions[i][0]);
4 }
5 op.value(M, left, 1.0); // Left BC.
6 op.neumann(M, right, {1}, 1.0);  // Right BC.
7 VectorXd solution = M.lu().solve(rhs);

As expected, MLSM is slower due to computation of shape functions, which are known in advance in FDM. However, counting that as part of the preprocessing and measuring only the part equivalent to FDM, it can be seen that the execution times for FDM and MLSM are the same for all practical purposes.

Time dependent 2D case

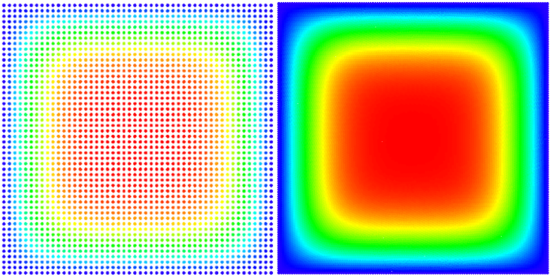
We solved the equation on a square $\Omega = [0, a] \times [0, a]$ with Dirichlet boundary conditions $ \left. u\right|_{\partial \Omega} = 0 $ and initial state $ u(t = 0) = 1$. An analytical solution for this domain is known \begin{equation} u(\vec{p}, t) = \sum_{\substack{n=1 \\ n \text{ odd}}}^\infty\sum_{\substack{m=1 \\ m \text{ odd}}}^\infty \frac{1}{\pi^2} \frac{16 a^2}{nm} \sin\left(\frac{\pi n}{a}p_x\right) \sin\left(\frac{\pi m}{a}p_y\right) e^{-\frac{\pi^2 (n^2+m^2)}{a^2}t} \end{equation}

Temperature contour polot after $t = 0.05$ and convergence regarding the number of nodes

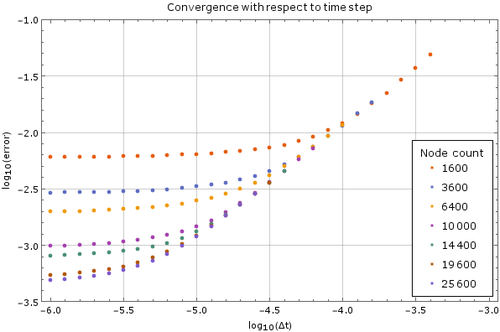
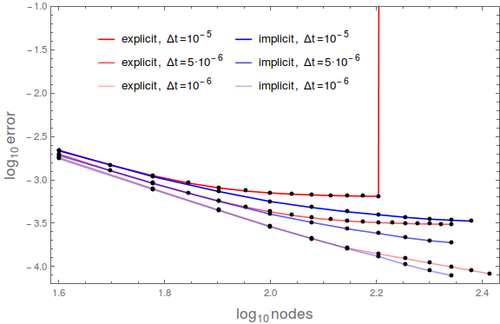
We tested the method with a fixed time step of $ \Delta t = 1\cdot 10^{-5}$ on a unit square ($a = 1$). Monomial basis of $6$ monomials was used and $12$ closest nodes counted as support for each node in one setup and in another 5 Guassians on 5 suport nodes. After more than $250$ nodes of discretization in each dimension the method diverges, which is expected. The stability criterion for diffusion equation in two dimensions is $\Delta t \leq \frac{1}{4} \Delta x^2$, where $\Delta x$ is the spatial discretization step in one dimension. In our case, at $250$ nodes per side, the right hand side yields $\frac{1}{4}\cdot\frac{1}{250}\cdot\frac{1}{250} = 4\times 10^{-6}$, so our method is stable within the expected region.

Convergence with respect to number of time steps and comaprios between implicit and explicit solution

And some more weird domains, just to have some fun ...

3D cases

For fun we can solve also few 3D cases. These are not part of any serious analysis and were made only for fun.

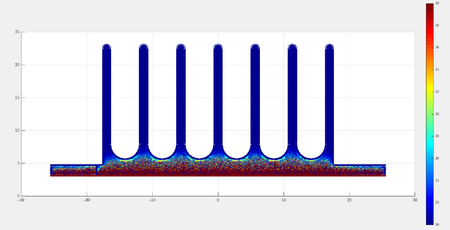
For starters a 3-dimensional example, where a CAD model for aluminium heat sink is discretized to obtain the domain description. Heat equation with $\alpha = 9.7 \cdot 10^{-5}]{m^2}{s}$, with no heat generation, i.e. $q = 0 {W}{m^3}$, with Dirichlet boundary conditions $u = \unit[100]{^\circ C}$ on the bottom surface and $u = \unit[20]{^\circ C}$ everywhere else.

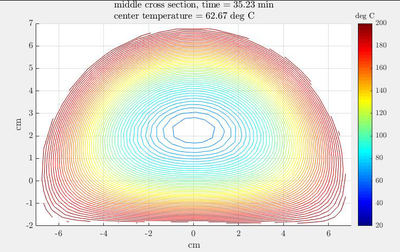
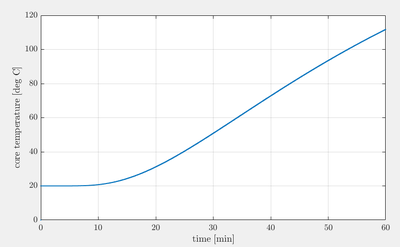
Next, example is simulation of baking Beef Wellington, where we followed therecipe. The simple 3D model is discretized with 70490 points and simulated for one hour with 1 s time step. The initial temperature is set to 20 deg C, the oven temperature is set to 200 deg C. Heat diffusivity of beef is found in the literature, the dimensions are 34 x 14 x 9 cm.

References

• Trobec R., Kosec G., Šterk M., Šarler B., Comparison of local weak and strong form meshless methods for 2-D diffusion equation. Engineering analysis with boundary elements. 2012;36:310-321; manuscript
• robec R., Kosec G., Parallel Scientific Computing, ISBN: 978-3-319-17072-5 (Print) 978-3-319-17073-2.
• Slak, J., Kosec, G.. Detection of heart rate variability from a wearable differential ECG device., MIPRO 2016, 39th International Convention, 2016, Opatija, Croatia, ISSN 1847-3938, pp 450-455.

This list might be incomplete, check also reference on the Main Page.