Natural convection between concentric cylinders
Click here to return back to Fluid Mechanics
Introduction
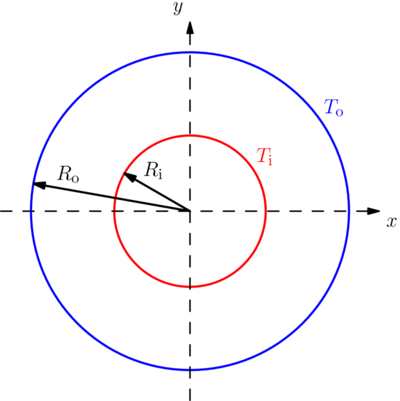
Another classical fluid flow benchmark is that of natural convection heat transfer in the annular space between concentric cylinders. This problem was first studied numerically by Kuehn and Goldstein (1975) using a stream function-vorticity formulation of the Navier-Stokes equations. Several assumptions are made in specifying the problem. First of all the flow is assumed to be invariant along the axis of the cylinders which leads to a two-dimensional flow configuration as schematically shown in the figure below. A constant property Boussinesq approximation is used. The buoyancy force may then be given as: \[ \b{g} = \left(\begin{matrix}g_x \\ g_y \end{matrix}\right) = \left(\begin{matrix}0 \\ g \beta \left(T - T_\mathrm{o}\right) \end{matrix}\right) \] where $g$ is the gravitational acceleration, $T$ the temperature at a point within the fluid, $T_\mathrm{o}$ the temperature of the outer cylinder and $\beta$ the thermal volumetric expansion coefficient. The inner cylinder is held at a constant temperature $T_\mathrm{i}$.
The equations to be solved are \begin{equation} \Delta \psi = \omega \end{equation} \begin{equation} \frac{\partial \omega}{\partial t} + u\frac{\partial \omega}{\partial x} + v\frac{\partial \omega}{\partial y} = \nu \Delta \omega + \left(\frac{\partial g_x}{\partial y} - \frac{\partial g_y}{\partial x}\right) \end{equation}
Sources
Kuehn, T. H., and R. J. Goldstein. "An experimental and theoretical study of natural convection in the annulus between horizontal concentric cylinders." Journal of Fluid mechanics 74, no. 4 (1976): 695-719.