Hertzian contact

Click on Solid Mechanics to go back.

Contact of Cylinders - the Hertz problem

Detailed discussions of this problem can be found in Hills and Nowells (1994) as well as Williams and Dwyer-Joyce (2001).

If two circular cylinders with radii $R_1$ and $R_2$ are pressed together by a force per unit length of magnitude $P$ with their axes parallel, then the contact patch will be of half-width $b$ such that \begin{equation} b = \sqrt{\frac{2PR}{\pi E^*}} \end{equation} where $R$ and $E^*$ are the reduced radius of contact and the contact modulus defined by \begin{equation} \frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2}, \end{equation} \begin{equation} \frac{1}{E^*} = \frac{1-{\nu_1}^2}{E_1} + \frac{1-{\nu_2}^2}{E_2}. \end{equation}

The resulting pressure distribution $p(x)$ is semielliptical, i.e., of the form \begin{equation} p(x) = p_0 \sqrt{1-\frac{x^2}{b^2}} \end{equation} where the peak pressure \begin{equation} p_0 = \sqrt{\frac{PE^*}{\pi R}}. \end{equation}

The coordinate $x$ is measured perpendicular to that of the cylinder axes. For the case of nominal contact between cylinders closed form analytical solutions are available.

The surfaces stresses are given by the equations:

500px

700px

700px

The surface stresses and stresses along the line of symmetry are shown in the following two graphs. The $x$ and $z$ coordinates are normalized with the contact width $b$.

300px 300px

Contact of cylinders under partial slip

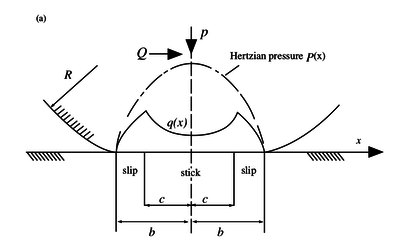
The second case we study is the application of a tangential force $Q$ to the previous problem. When the tangential force is less than the limiting force of friction, i.e., \[|Q| < \mu P,\] sliding motion will not occur but the contact will be divided into regions of slip and stick zones that are unknown a priori. For the case of cylinders the analysis is given in Hills & Nowell (1994), p. 44.

Besides the normal traction $p(x)$ we know have an additional shear traction given by \begin{equation} q(x) = \begin{cases} -\mu p_0 \sqrt{1 - \frac{x^2}{b^2}}, \quad c \leq |x| \leq b \\ -\mu p_0 \left(\sqrt{1 - \frac{x^2}{b^2}} - \frac{c}{b}\sqrt{1 - \frac{x^2}{c^2}}\right), \quad |x| < c \end{cases} \end{equation} where $b$ is the half-width of the whole contact, and $c$ the half-width of the central sticking region. The width of the central zone, i.e. the value of dimension $c$ is dependent on the applied tangential force $Q$: \begin{equation} \frac{c}{b} = \sqrt{1 - \frac{Q}{\mu P}} \end{equation}

The distributions $q(x)$ and $p(x)$ as well as the widths of the stick and slip zones can be seen in the image below.