Heart rate variability detection
We used MLS and WLS aproximation to extract heart rate variability from a wearable ECG sensor. Full paper available for download here. Presentation available for download here.
The code can be found in /EKG/detect.cpp.
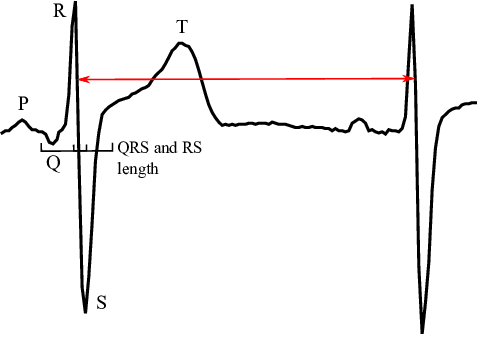
Figure 1 shows how we detected beat to beat times from an actual heartbeat.
A slightly abridged version of the paper is presented below.
Contents
Detection of heart rate variability
from a wearable differential ECG device
Jure Slak, Gregor Kosec, Jožef Stefan Insitute, Department of Communication Systems, Ljubljana.
Abstract
The precise heart rate variability is extracted from an ECG signal measured by a wearable sensor that constantly records the heart activity of an active subject for several days. Due to the limited resources of the wearable ECG device the signal can only be sampled at relatively low, approximately $100$ Hz, frequency. Besides low sampling rate the signal from a wearable sensor is also burdened with much more noise than the standard $12$-channel ambulatory ECG, mostly due to the design of the device, i.e. the electrodes are positioned relatively close to each other, and the fact that the subject is active during the measurements. To extract heart rate variability with $1$ ms precision, i.e. $10$ times more accurate than the sample rate of the measured signal, a two-step algorithm is proposed. In first step an approximate global search is performed, roughly determining the point of interest, followed by a local search based on the Moving Least Squares approximation to refine the result. The methodology is evaluated in terms of accuracy, noise sensitivity, and computational complexity. All tests are performed on simulated as well as measured data. It is demonstrated that the proposed algorithm provides accurate results at a low computational cost and it is robust enough for practical application.
Introduction
It is well known that the morphology of ECG signals changes from beat to beat as a consequence of physical activity, sensations, emotions, breathing, etc. of the subject. The most straightforward measure of these changes is the heart rate variability (HRV), i.e. small variations of beat duration. HRV characterizes the timings of hearth cells repolarization and depolarization processes. The HRV is typically determined by measuring the intervals between two consecutive R-waves (RRI) or intervals between R and T waves (RTI). Several vital signals can be identified from the HRV and therefore it is often used as a health status indicator in different fields of medicine, e.g. neurology, cardiac surgery, heart transplantation and many more. Typical HRV values of healthy subjects are approximately $40$ ms for RRI and $2$ ms for RTI (see Figure 2). Therefore it is important to detect considered waves with at least $1$ ms accuracy for practical use. This paper deals with the detection of HRV in ECG signal provided by a Wearable ECG Device (WECGD) that is paired with a personal digital assistant (PDA) via Bluetooth Smart protocol. The WECGD, due to the hardware limitations, only measures the signal, while the PDA takes care of data visualization, basic analysis and transmission of the data to a more powerful server for further analyses. In contrast to a standard ambulatory $12$-channel ECG measurement, where trained personnel prepare and supervise the measurement of subject at rest, the WECGD works on a single channel, the subject is active and since the WECGD is often placed by an untrained user its orientation might be random, resulting in additional decrease of signal quality. In order to maintain several days of battery autonomy The WECGD also records the heart rate with significantly lower frequencies and resolution in comparison to ambulatory measurements. All these factors render the standard ECG analysis algorithms ineffective. In this paper we analyse a possible local, i.e. only short history of measurement data is required, algorithm for detection of heart rate variability with $1$ ms precision of a signal recorded with $120$ Hz.
Detection method
In order to evaluate the HRV, the characteristic point of each heart beat has to be detected in the signal, which is provided as values of electric potential sampled with a frequency $120$ Hz. Since the HRV is computed from differences of consequent characteristic points the choice of the characteristic point does not play any role, as long as it is the same in every beat. In this work we choose to characterise the beat with a minimal first derivative, in another words, we seek the points in the signal with the most violent drop in electric potential (Figure 2) that occurs between R and S peaks.
The detection method is separated in two stages, namely global and local. The goal of the global method is to approximately detect the characteristic point, while the local method serves as a fine precision detection, enabling us to detect HRV with much higher accuracy.
Coarse global search
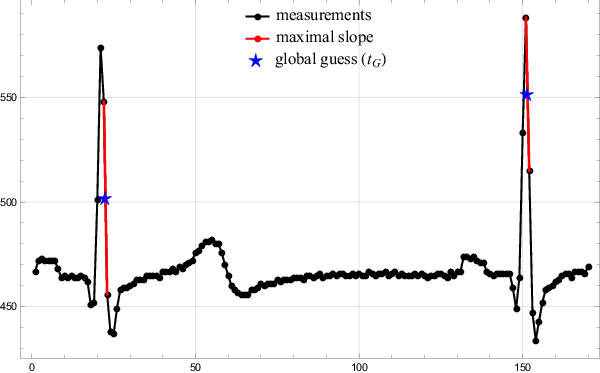
In the first step the algorithm finds a minimal first derivative of a given signal on a sample rate accuracy, i.e. $\frac{1}{\nu}$. The global search method is next to trivial. The algorithm simply travels along the signal, calculating the discrete derivative and storing the position of minimal values found so far. Since the points are sampled equidistantly, minimizing $\frac{\Delta y}{\Delta t}$ is equal to minimizing $\Delta y$. The middle of the interval where the largest drop was detected is taken as the global guess $t_G$. The results of the global search are presented in Figure 3.
Fine local search
The global search provides only coarse, limited to sample points, positions of the characteristic points. To push accuracy beyond $1/\nu$, the signal has to be represented also in between the sample points. A monomial approximation function based on a Moving Least Squares approach is introduced for that purpose.
The value of the electrical potential at arbitrary time $t_0$ is approximated. Denote the vector of $n$ known values near $t_0$ by $\boldsymbol{f}$ (called support), and the times at which they were measured by $\boldsymbol{t}$. The approximation $\hat{f}$ of $\boldsymbol{f}$ is introduced as a linear combination of $m$ in general arbitrary basis functions $(b_j)_{j=1}^m$, however in this work only monomials are considered. \[\hat{f} = \sum_{j=1}^m\alpha_jb_j \]
The most widely used approach to solve above problem and find the appropriate $\hat{f}$ is to minimize the weighted 2-norm of the error, also known as the Weighted Least Squares (WLS) method. \[ \|\boldsymbol{f} - \hat{f}(\boldsymbol{t})\|_w^2 = \sum_{i=1}^n (f_i -\hat{f}(t_i))^2 w(t_i), \] In the above equation $w$ is a nonnegative weight function.
The only unknown quantities are the $m$ coefficients $\boldsymbol{\alpha}$ of the linear combination, which can be expressed as a solution of an overdetermined linear system $W\!B\boldsymbol{\alpha} = W\!\boldsymbol{f}$, where $W$ is the $n\times n$ diagonal weight matrix, $W_{ii} = \sqrt{w(t_i)}$ and $B$ is the $n\times m$ collocation matrix, $B_{ij} = b_j(t_i)$. There are different approaches towards finding the solution. The fastest and also the least stable and accurate is to solve the Normal System $B^\mathsf{T} W^\mathsf{T} WB\boldsymbol{\alpha} = B^\mathsf{T} W^\mathsf{T} W\boldsymbol{f}$, a more expensive but also more stable is via QR decomposition, and finally the most expensive and also the most stable is via SVD decomposition. The resulting vector $\boldsymbol{\alpha}$ is then used to calculate $\hat{f}(t)$ for any given $t$. The derivatives are approximated simply by differentiating the approximating function, $\hat{f}' = \sum_{j=1}^m\alpha_jb_j'$.
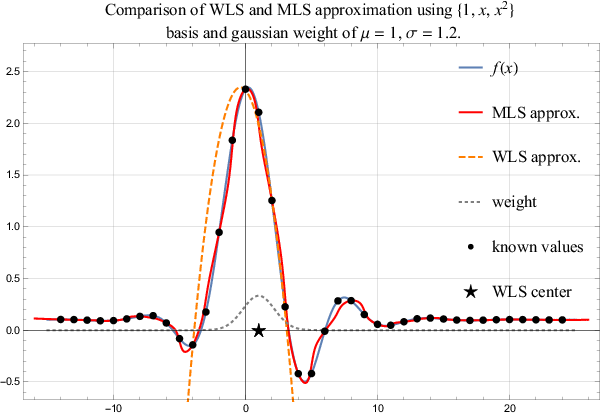
The WLS approximation weights the influence of support points using the weight function $w$. Usually, such a weight is chosen that points closest to $t_0$ are more important in the norm in comparison to the nodes far away. Naturally such approximation is valid only as long as the evaluation point is close to the $t_0$. A more general approach is a Moving Least Square (MLS) approximation, where coefficients $\alpha$ are not spatially independent any more, but are recomputed for each evaluation point. Naturally, such an approach is way more expensive, but also more precise. A comparison of both methods, i.e. WLS and MLS, is shown in Figure 4.