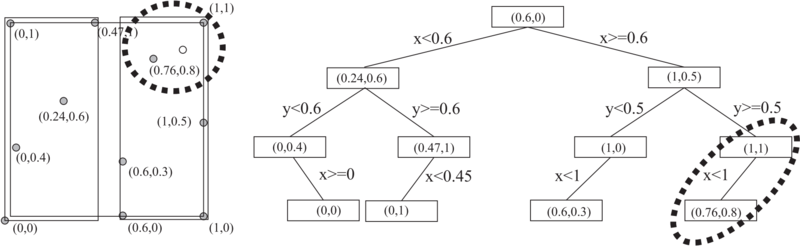
K-d tree

In structured meshes, neighborhood relations are implicitly determined by the mapping from the physical to the logical space. In unstructured mesh based approaches, support domains can be determined from the mesh topology. However, in meshless methods, the nearest neighboring nodes in $\Omega_S$ are determined with various algorithms and specialized data structures, we use kD Tree.

The input to Algorithm is a list of $(n_S +1)$ nearest nodes to ${\bf x}$. A naive implementation of finding these nodes could become quite complex if implemented with classical sorting of all nodal distances. Regarding the number of nodes $N$, it approaches the quadratic computational complexity. However, by using efficient data structures, e.g. quadtree, R tree or kD tree (2D tree for 2D domains), the problem becomes tractable. The strategy is to build the data structure only once, before the solution procedure. During the solution, the support nodes of the desired points will then be found much faster.