De Vahl Davis natural convection test

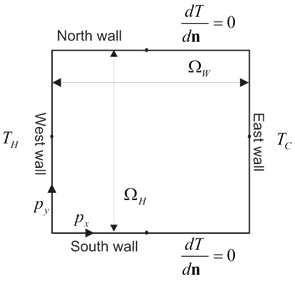
The classical de Vahl Davis benchmark test is defined for the natural convection of the air ($\Pr =0.71$) in the square closed cavity (${{\text{A}}_{\text{R}}}=1$). The only physical free parameter of the test remains the thermal Rayleigh number. In the original paper [1] de Vahl Davis tested the problem up to the Rayleigh number ${{10}^{6}}$, however in the latter publications, the results of more intense simulations were presented with the Rayleigh number up to ${{10}^{8}}$. Lage and Bejan [2] showed that the laminar domain of the closed cavity natural convection problem is roughly below $\text{Gr1}{{\text{0}}^{9}}$. It was reported [3, 4] that the natural convection becomes unsteady for $\text{Ra}=2\cdot {{10}^[5]}$. Here we present a MLSM solution of the case. [1] de Vahl Davis G. Natural convection of air in a square cavity: a bench mark numerical solution. Int J Numer Meth Fl. 1983;3:249-64. [2] Lage JL, Bejan A. The Ra-Pr domain of laminar natural convection in an enclosure heated from the side. Numer Heat Transfer. 1991;A19:21-41. [3] Janssen RJA, Henkes RAWM. Accuracy of finite-volume disretizations for the bifurcating natural-convection flow in a square cavity. Numer Heat Transfer. 1993;B24:191-207. [4] Nobile E. Simulation of time-dependent flow in cavities with the additive-correction multigrid method, part II: Apllications. Numer Heat Transfer. 1996;B30:341-50.

. Figure 1: Scheme of the de Vahl Davis benchmark test

The snippet of the openMP parallel MLSM code for an explicit ACM method with CBS looks like: (full examples, including implicit versions, can be found under the examples in the code repository Main Page).

 1 //transport equations
 2         #pragma omp parallel for private(i) schedule(static)
 3         for (i=0;i<interior.size();++i) {
 4             int c=interior[i];
 5             //Navier-Stokes
 6             v2[c] = v1[c] + O.dt * ( - 1/O.rho    * op.grad(P1,c)
 7                                      + O.mu/O.rho * op.lap(v1, c)
 8                                      -              op.grad(v1,c)*v1[c]
 9                                      + O.g*(1 - O.beta*(T1[c] - O.T_ref))
10             );
11             //heat transport
12             T2[c] = T1[c] + O.lam / O.rho / O.c_p * O.dt * op.lap(T1, c)
13                     -O.dt*O.rho*O.c_p * v1[c].transpose()*op.grad(T1,c) ;
14         }
15         //heat Neumann condition
16         #pragma omp parallel for private(i) schedule(static)
17         for (i=0;i<top.size();++i) {
18             int c = top[i];
19             T2[c] = op.neumann(T2, c, vec_t{0, 1}, 0.0);
20         }
21 
22         #pragma omp parallel for private(i) schedule(static)
23         for (i=0;i<bottom.size();++i) {
24             int c = bottom[i];
25             T2[c] = op.neumann(T2, c, vec_t{0, -1}, 0.0);
26         }
27 
28         //Mass continuity
29         #pragma omp parallel for private(c) schedule(static)
30         for (i=0; i<domain.size(); ++i) {
31 
32             P2[i] = P1[i] - O.dl * O.dt * O.rho * op.div(v2, i) +
33                     O.dl2 * O.dl * O.dt * O.dt * op.lap(P1, i);
34         }
35         //time step
36         v1.swap(v2);
37         P1.swap(P2);
38         T1.swap(T2);