Scattering from an infinite cylinder

Back to Computational electromagnetics.

Case

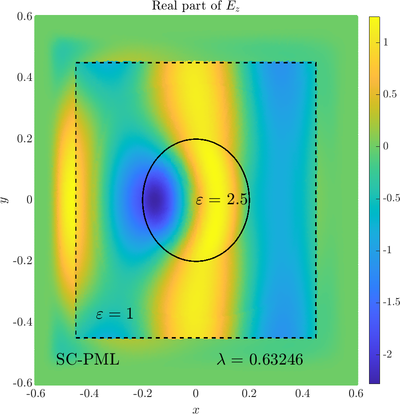
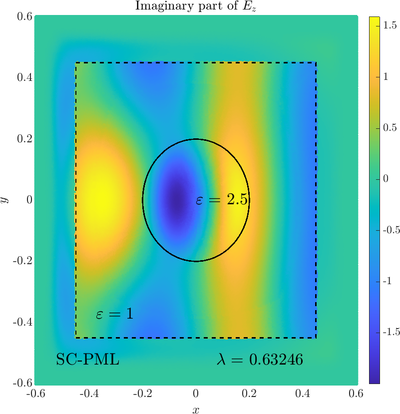
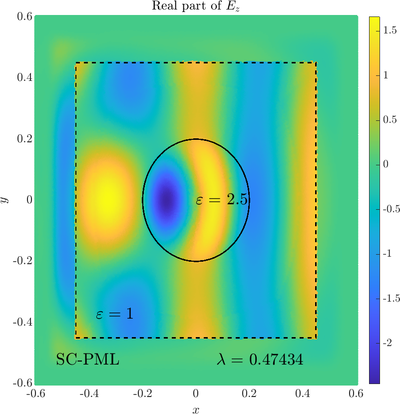
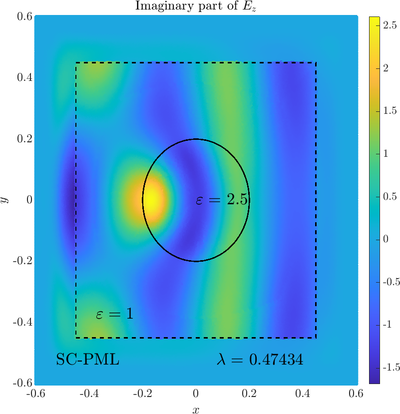
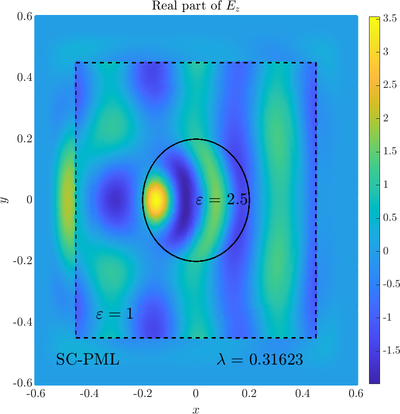
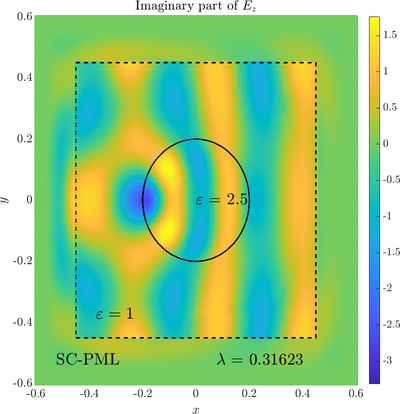
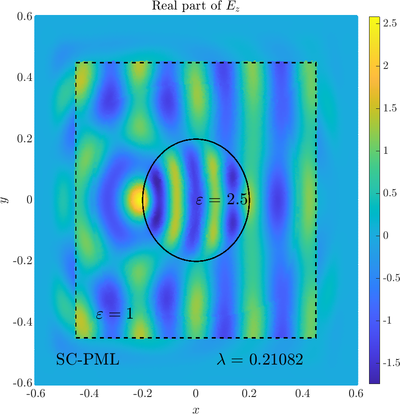
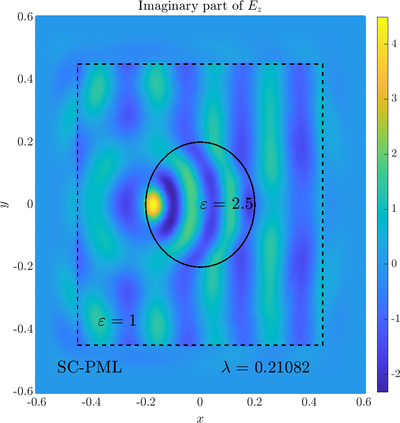
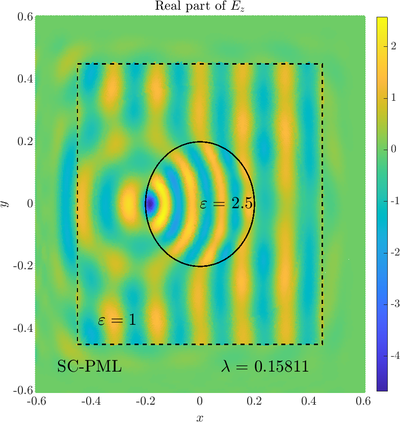
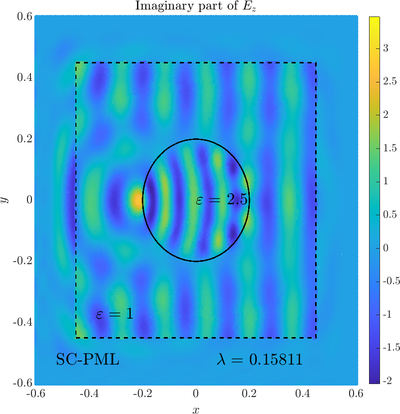
$\newcommand{\eps}{\varepsilon} \newcommand{\dpar}[2]{\frac{\partial #1}{\partial #2}} \newcommand{\ddpar}[2]{\frac{\partial^2 #1}{\partial #2^2}} \def\doubleunderline#1{\underline{\underline{#1}}}$ As a simple two dimensional case let us consider a plane wave scattering on a dielectric cylinder. This case is important for two reasons, firstly, it shows how to encode the incident wave into the boundary between the cylinder and free space and thus calculate only with the scattered field outside. It shows how to use analytic expressions to represent sources with known analytical solutions, this is especially useful when dealing with point sources. This case is important for two reasons. Firstly we will see how we can describe the solution in terms of scattered fields only, by including the incident wave in the boundary conditions. Secondly the problem has a relatively simple analytical solution in terms of Hankel funitons and can be used as a benchmark case.The problem is defined in two domains, inside and outside the cylinder, we are solving the following system of two PDE that are coupled on the inside boundary

$$\begin{align} \nabla^2 E_z^{int} +\eps_r \frac{\omega^2}{c_0^2}\thinspace E_z^{int} = 0 \qquad &\text{in} \quad D \label{eq:inner} \\ \nabla^2 E_z^s + \frac{\omega^2}{c_0^2}E_z^s = 0 \qquad & \text{outside} \quad D \label{eq:outer} \end{align}$$ The field $E_z^{int}$ is the total field inside, $E_z^s$ is only the scattered part of $E_z$ Outside the cylinder. The boundary conditions are $$\begin{equation} E_z^{int} - E_z^{s} =E_z^{inc} \qquad \text{on} \quad \partial D \label{eq:BC1}, \qquad \text{and} \qquad \dpar{E_z^{int}}{n} - \frac{1}{\eps_r}\dpar{E_z^{s}}{n} = \dpar{E_z^{inc}}{n} \qquad \text{on} \quad \partial D. \end{equation}$$ The incident field $E_z^{inc}$ has an analytical form in our case a plane wave $e^{ikx}$, since it has a nice closed form we know its derivatives and the boundary conditions are nicely expressed. Around the computational domain we use a PML to simulate an infinite domain.

 1 	// Construct system
 2 	double l_in = epsr*std::pow(omega/c0, 2.0);
 3 	double l_out = std::pow(omega/c0, 2.0);
 4 	for (int i : cyl_dom.interior()){
 5 		op_inner.lap(i) + l_in*op_inner.value(i) = 0.0;
 6 	}
 7 	for (int i : outer_inter){
 8 		op_outer.lap(i) + l_out*op_outer.value(i) = 0.0;
 9 	}
10 	for (int c = 0; c < interface_c_idx.size(); ++c){
11 		int i = interface_c_idx[c]; // cyl index
12 		int j = interface_o_idx[c]; // outer index
13 		Vec2d pos = cyl_dom.pos(i);
14 		double x = pos[0];
15 		double y = pos[1];
16 
17 		// calculate normal derivative of the source funciton at the i-th node
18 		// get normal, must point out of the cylinder
19 		Vec2d normal = cyl_dom.normal(i);
20 		std::complex<double> incident = std::exp(1.0_i*k0*(x*std::cos(t0)+y*std::sin(t0)));
21 		std::complex<double> din_dx = 1.0_i*k0*std::cos(t0)*std::exp(1.0_i*k0*(x*std::cos(t0)+y*std::sin(t0)));
22 		std::complex<double> din_dy = 1.0_i*k0*std::sin(t0)*std::exp(1.0_i*k0*(x*std::cos(t0)+y*std::sin(t0)));
23 		std::complex<double> dui_dn = normal[0]*din_dx + normal[1]*din_dy;
24 
25 		// continuity of the fields, and the incident field
26 		op_inner.value(i) + (-1)*op_outer.value(j, Nouter + i) = incident;
27 
28 		// continuity of derivatives
29 		op_outer.neumann(j, outer_dom.normal(j)) + (1/epsr)*op_inner.neumann(i, cyl_dom.normal(i), j - Nouter)
30 				= dui_dn;
31 	}
32 	// SC-PML - where either x or y is constant
33 	for (int i : PML){
34 		1.0/(sw[i]*sw[i])*op_outer.lap(i) + l_out*op_outer.value(i) +
35 		((-1.0)/(sw[i]*sw[i]*sw[i])*exop.d1(sw, 0, i)*op_outer.der1(i, 0)
36 			+(-1.0)/(sw[i]*sw[i]*sw[i])*exop.d1(sw, 1, i)*op_outer.der1(i, 1)) = 0.0;
37 	}
38 	for (int i: outer_bnd){
39 		op_outer.value(i) = 0.0;
40 	}

Analytical solution

The solution to this problem is sought in terms of sums of cylindrical harmonics. The incident wave is a plane wave $\b E_i = \hat e_z E_0 e^{-ikx}$ and can be decomposed into Bessel functions of the first kind as

$$\begin{equation} \mathbf{E}_{i}=\widehat{z} E_{0} e^{-i k_{0} x}= \widehat{z} E_{0} \sum_{n=-\infty}^{\infty} i^{-n} J_{n}\left(k_{0} \rho\right) e^{i n \phi}. \end{equation}$$ The scattered field is a sum of Hankel functions so it satisfies the Sommerfeld radiation condition $$\begin{equation} \mathbf{E}^{s}=\widehat{z} E_{0} \sum_{n=-\infty}^{\infty} i^{-n} a_{n} H_{n}^{(2)}\left(k_{0} \rho\right) e^{i n \phi}, \quad \rho \geq a \end{equation}$$ and finally the total field is again a sum ob Bessel functions of the first kind $$\begin{equation} \mathbf{E}^{t}=\widehat{z} E_{0} \sum_{n=-\infty}^{\infty} i^{-n} b_{n} J_{n}\left(k_{1} \rho\right) e^{i n \phi}, \quad \rho \leq a. \end{equation}$$ The boundary conditions for the field and its derivative on the boundary between the cylinder and free space surrounding it give two expressions $$\begin{equation} J_{n}\left(k_{0} a\right)+a_{n} H_{n}^{(2)}\left(k_{0} a\right)=b_{n} J_{n}\left(k_{1} a\right) \end{equation}$$ and $$\begin{equation} k_0 J^{\prime}_{n}\left(k_{0} a\right)+ k_0 a_{n} H_{n}^{\prime(2)}\left(k_{0} a\right)=k_1 b_{n} J^{\prime}_{n}\left(k_{1} a\right). \end{equation}$$ Which give the coefficients $a_n$ and $b_n$ in the above expansions as $$\begin{equation} a_{n}=-\frac{J_{n}\left(k_{0} a\right)-\Gamma_{h} J_{n}^{\prime}\left(k_{0} a\right)}{H_{n}^{(2)}\left(k_{0} a\right)-\Gamma_{h} H_{n}^{(2)^{\prime}}\left(k_{0} a\right)}, \end{equation}$$ where $$\begin{equation} \Gamma_{h}=\frac{Z_{0}}{Z_{1}} \frac{J_{n}\left(k_{1} a\right)}{J_{n}^{\prime}\left(k_{1} a\right)} \end{equation}$$ and $$\begin{equation} b_n = \frac{J_n(k_0a)}{J_n(k_1a)} + a_n \frac{H_n^{(2)}(k_0a)}{J_n(k_1a)}. \end{equation}$$

Results