Electromagnetic scattering

In this example we will show how to solve an electromagnetic scattering problem in Medusa. The example uses both complex numbers as well as domain coupling, so we recommend firstly reading tutorials on Coupled domains and Complex-valued problems.

Anisotropic cylinder

Let us first quickly derive the problem we are about to solve. Beginning with the electromagnetic wave equation in anisotropic media

$$\label{eq:frekaniwave} \nabla \times \left( \underline{\varepsilon}^{-1} \nabla \times \boldsymbol{H} \right) = \omega^2 \mu_0 \varepsilon_0 \underline{\mu} \boldsymbol{H},$$ where $\underline{\varepsilon}$ is the relative dielectric tensor, and $\underline{\mu}$ is the magnetic permeability tensor of the anisotropic material

$$\label{eq:relepsmi} \underline{\varepsilon} = \begin{pmatrix} \varepsilon_{xx} & \varepsilon_{xy} & \varepsilon_{xz} \\ \varepsilon_{yx} & \varepsilon_{yy} & \varepsilon_{yz} \\ \varepsilon_{zx} & \varepsilon_{zy} & \varepsilon_{zz} \end{pmatrix} , \qquad \underline{\mu} = \begin{pmatrix} \mu_{xx} & \mu_{xy} & \mu_{xz} \\ \mu_{yx} & \mu_{yy} & \mu_{yz} \\ \mu_{zx} & \mu_{zy} & \mu_{zz} \end{pmatrix}.$$

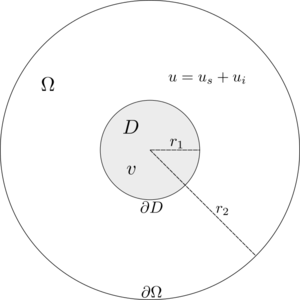
Let $D \subset \R^2$ be the cross section of an infinitely long anisotropic dielectric cylindrical scatterer with its axis alligned with the $z$-axis, surrounded by a free space, with an outward normal $n$ on boundary $\partial D$. The cylinder is isotropic along its axis, and is excited by an $e^{i \omega t}$ time-harmonic plane wave with $\b{TM}^z$ polarization, with $\omega$ standing for its angular frequency. Let $v \in C^2(\C)$ denote the complex valued field inside the scatterer and $u \in C^2(\C)$ the field outside of the scatterer. Field $u$ can be further decomposed into the incident $u^i$ and the scattered field $u^s$.

The fields $u^s$ and $v$ must satisfy the set of PDE

$$\begin{align*} \nabla \cdot A \nabla v + \epsilon_r k^2 \thinspace v = 0 \qquad &\text{in} \quad D \label{eq:inner} \\ \nabla^2 u^s + k^2 \thinspace u^s = 0 \qquad &\text{in} \quad \Omega \setminus D \label{eq:outer} \end{align*}$$ with boundary conditions $$\begin{align*} v - u^s =u^i \qquad &\text{on} \quad \partial D \label{eq:BC1} \\ \frac{\partial v}{\partial n_A\!\!\!} - \frac{\partial u^s}{\partial n} = \frac{\partial u^i}{\partial n} \qquad &\text{on} \quad \partial D \label{eq:BC2} \\ \frac{\partial u^s}{\partial n} + \left( ik + \frac{1}{2r_2} \right)u^s = 0 \quad &\text{on} \quad \partial \Omega \end{align*}$$ where $k = \omega \sqrt{\mu_0 \epsilon_0} = \frac{2 \pi}{\lambda}$ is the wave number of free space, $\mu_0$ and $\epsilon_0$ are magnetic permeability and electric permittivity of free space, while $\epsilon_r$ is the relative electric permittivity of the scatterer. Relative magnetic permeability matrix $A$ is of the following form $$\begin{equation*} A = \frac{1}{\mu_{xx}\mu_{yy} - \mu_{xy}^2} \begin{pmatrix} \mu_{xx} & \mu_{xy} \\ \mu_{xy} & \mu_{yy} \end{pmatrix} \end{equation*}$$ and the anisotropic normal derivative is calculated as $$\begin{equation*} \frac{\partial v}{\partial n_A\!\!\!} = n \cdot A \nabla {v}. \end{equation*}$$