Coupled domains

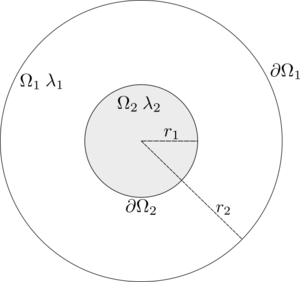
In this example we will show how one can solve coupled problems with Medusa library. We will solve the stationary heat equation on concentric circles where the thermal conductivity $\lambda$ is different for each circle. The inner circle will be heated up, while the outside temperature will be held at zero.

In mathematical terms, we want to solve the system \begin{align*} -\Delta v = q_0 \qquad &\text{on} \quad \Omega_2 \\ \Delta u = 0 \qquad &\text{on} \quad \Omega_1 \end{align*}

With boundary conditions \begin{align*} u = 0 \qquad &\text{on} \quad \partial \Omega_1 \\ u = v \qquad &\text{on} \quad \partial \Omega_2 \\ \frac{\partial u}{\partial n_1} = \frac{\partial v}{\partial n_2} \qquad &\text{on} \quad \partial \Omega_2 \\ \end{align*} We will see that the task is quite simple using Medusa, first we create the domains $\Omega_1$ and $\Omega_2$

 1     BallShape<Vec2d> inner_shape(0, r1);
 2     BallShape<Vec2d> outer_circle(0, r2);
 3     auto outer_shape = outer_circle - inner_shape;
 4 
 5     DomainDiscretization<Vec2d> outer = outer_shape.discretizeBoundaryWithStep(h);
 6     DomainDiscretization<Vec2d> inner(inner_shape);
 7 
 8     // Indices of nodes in outer domain that constitute outer and common boundary.
 9     auto common_bnd = outer.positions().filter([=](const Vec2d& p) { return std::abs(p.norm() - r1) < 1e-5; });
10     auto outer_bnd = outer.positions().filter([=](const Vec2d& p) { return std::abs(p.norm() - r2) < 1e-5; });

In the code above, we constructed two BallShapes and calculated their difference, giving us the shape of an annulus. We use the annulus shape to obtain the outer domain discretization, and the BallShape with the smaller radius to construct the inner domain discretization. Some care needs to be given to filling the domains, we need to be careful because we want the domains to share the nodes on the boundary $\partial \Omega_2$. Notice that as we discretized the boundary of the annulus we already filled both $\partial \Omega_1$ and $\partial \Omega_2$. Hence, we filter the boundary nodes of the outer domain into the outer boundary and the common boundary, this will prove useful later on.

 1     // Maps node indices of outer domain to their corresponding indices in the inner domain.
 2     Range<int> outer_to_inner(outer.size(), -1);
 3     for (int i : common_bnd) {
 4         int idx = inner.addBoundaryNode(outer.pos(i), -2, -outer.normal(i));
 5         outer_to_inner[i] = idx;
 6     }
 7 
 8     GeneralFill<Vec2d> fill_engine; fill_engine.seed(1);
 9     outer.fill(fill_engine, h); // this is the annulus
10     inner.fill(fill_engine, h); // this is the inner circle

The snippet above shows how to add the the nodes on the common boundary to the inner domain. The normals of the shared boundary nodes belonging to the inner domain must point into the opposite direction as the normals belonging to the shared boundary nodes in the outer domain. After this is done insides of both domains are filled.