k-d tree
In structured meshes, neighborhood relations are implicitly determined by the mapping from the physical to the logical space. In unstructured mesh based approaches, support domains can be determined from the mesh connectivity relations. However, in meshless methods, the stencil/support nodes are usually chosen as the nearest $n$ visible nodes.
In order to compute nearest neighbors effectively, fast spatial search structures have been developed, such as octree, ball tree, cover tree and $k$-d tree. All of these structures first take a list of $N$ points and build a search structure, enabling subsequent queries for $n$ nearest neighbors to be answered in $O(n\log N)$ time. The $k$-d tree structure is describe below to give reader a basic idea of how such spatial structures store data.
A $k$-d tree is a binary tree which uses hyperplane space partitioning to divide points into subgroups (subtrees). The plane is chosen based on the depth of the node in a tree. At depth $k$, the $k$-th axis (dimenison) is used to divide the remaining points. Example: in 3 dimensions we have $x$, $y$ and $z$ axes. At root level we decide to divide points according to their $x$ values (we could also do it according to $y$ or $z$ values). Usual criterion for division of points is the median. Thus, at root level, we look for median point by looking at $x$ coordiantes of all points. We put the median point into the root leaf. Remaining points are put into the left and right subtrees. We put the points which have smaller $x$ coorinate into the left subtree and points which have larger $x$ coordinate into the right subtree (or vice versa). We construct the two children nodes of the root from the two subgroups we just created. The procedure is the same, except that we divide the space according to $y$ or $z$ coordinate. We continue this way until we run out of points. The axes used for median search are periodically repeating.
Often, dynamic search structures are needed as well, which support node insertion and removal. In the beginning we were using ANN and libssrckdtree libraries for static and dynamic spatial search structures, respectively. Later, we tested four different publicly available C++ libraries that support at least static spatial search:
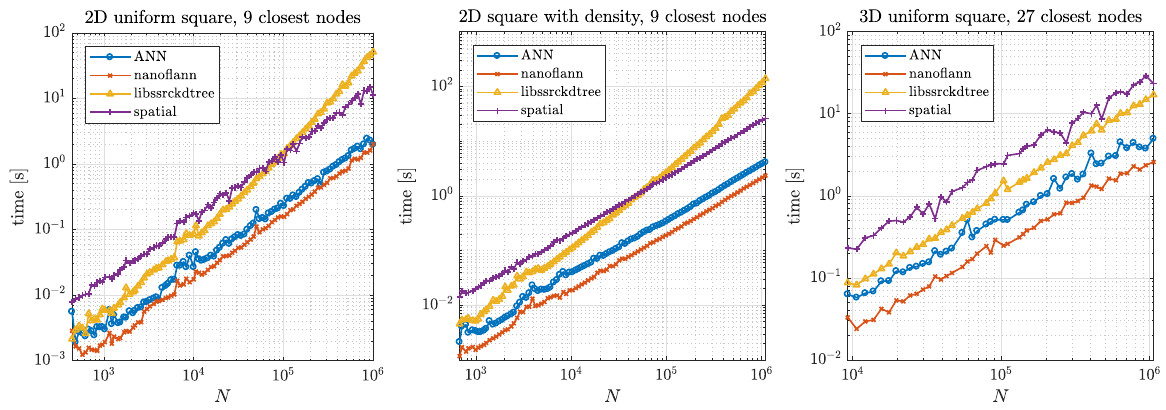
Two typical usage examples for these structures were tested. First, we tested a typical example of finding support domains of $n$ nodes for all nodes, which includes building a tree from a set of points and finding $n$ closest nodes for each point. The results are shown below.
Second, we tested how the structures performed during the node generation process, as described in Positioning of computational nodes page. Results are shown in figure below.
Besides speed, which was the main factor, we also considered the number of dependencies a library has and how general it is regarding distances and data types. Overall, we decided to use the nanoflann library in medusa.
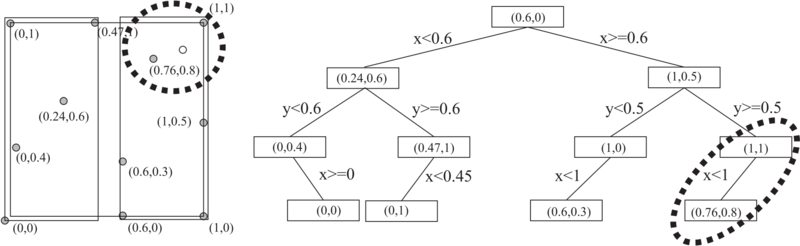
Let us illustrate the whole procedure with a simple example of a 2D tree for eleven nodes, with node numbers and coordinates listed in the first and the second column of Table \ref{tab:kD_nodes} and attached to the corresponding dots on the unit square in the left part of Figure \ref{fig.2D_treegraph}.
{\begin{table}[h] \centering \begin{tabular}{|c|c|c|c|c|c|} \hline Node number&Unsorted & Sorted by '"`UNIQ-MathJax24-QINU`"' & Sorted by '"`UNIQ-MathJax25-QINU`"' & Sorted by '"`UNIQ-MathJax26-QINU`"' & Bucket\\ \hline 1&(0,0)&(0,0)&(0,0)&(0,0)& \bf (0,0) \\ \hline 2&(0.6,0)&(0,0.4)&(0,0.4)&\bf (0,0.4)& \\ \hline 3&(1,0)&(0,1)&\bf (0.24,0.6)& & \\ \hline 4&(0,0.4)&(0.24,0.6)&(0,1)&(0,1)& \bf (0,1) \\ \hline 5&(0.6,0.3)&(0.47,1)&(0.47,1)&\bf (0.47,1)&\\ \hline 6&(1,0.5)&\bf (0.6,0)& & &\\ \hline 7&(0.24,0.6)&(0.6,0.3)&(1,0)&(0.6,0.3)&\bf (0.6,0.3)\\ \hline 8&(0.76,0.8)&(0.76,0.8)&(0.6,0.3)&\bf (1,0)&\\ \hline 9&(0,1)&(1,0)&\bf (1,0.5)& &\\ \hline 10&(0.47,1)&(1,0.5)&(0.76,0.8)&(0.76,0.8)&\bf (0.76,0.8)\\ \hline 11&(1,1)&(1,1)&(1,1)&\bf (1,1)&\\ \hline \end{tabular} \caption{The list of eleven nodes (1st column) determined with coordinates (2nd column), after sorting by $x$ (3rd column), after sorting sub lists by $y$ (4th column) and after sorting sub sub lists by $x$ again (5th column). The nodes nearest to medians are shown in bold.} \label{tab:kD_nodes} \end{table}
In the first step of 2D tree construction, the list of nodes is sorted by their $x$ coordinate, which is shown in third column of Table \ref{tab:kD_nodes}. Then a node with median coordinate, $x = 0.6$ in our case (shown in bold), is selected as the root of the first level of the 2D tree. If there is more than one such node, any one can be selected. The sorted set in column 3 is split into two parts, the one for $x$ below the median, i.e. $x < 0.6$, and the one for $x$ above or equal the median, i.e. $x\geq 0.6$. The two sub sets of nodes are shown in the left part of Figure \ref{fig.2D_treegraph} within two distinct rectangles, and on the right side of Figure \ref{fig.2D_treegraph} as the left and the right part of the 2D tree.
In the second step, the two sub lists of nodes are sorted by their $y$ coordinate, which is shown in fourth column of Table \ref{tab:kD_nodes}. The median coordinates $y$ are $0.6$ and $0.5$, respectively. The corresponding nodes $(0.24,0.6)$ and $(1,0.5)$ are taken as roots for the second level of 2D tree and are shown in bold and used to further split the tree. The resulting four sub sub sets of nodes are shown in the right side of Figure \ref{fig.2D_treegraph} as nodes on the lower two levels of the 2D tree.
Finally, the sub sub lists are sorted again by their $x$ coordinate, with the result shown in fifth column. Four roots are obtained with the coordinate $x$ nearest to medians, namely the nodes $(0,0.4)$, $(0.47,1)$, $(1,0)$, and $(1,1)$. The remaining nodes of the last level of the 2D tree, also termed the bucket, are $(0,0)$, $(0,1)$, $(0.6,0.3)$, and $(0.76,0.8)$. In practical cases, the refinement of the tree stops sooner, when its leaves are represented by list of several nodes, because such a fine grained distribution of leaves as in the presented example is often not beneficial from the computational efficiency point of view.
References
- Trobec R., Kosec G., Parallel scientific computing: theory, algorithms, and applications of mesh based and meshless methods: Springer; 2015.