Difference between revisions of "Solving sparse systems"

From Medusa: Coordinate Free Mehless Method implementation
Jump to: navigation, search
Line 47: Line 47:
  
 
'''"When using sparse matrices, best performance is achied for a row-major sparse matrix format.<br>Moreover, in this case multi-threading can be exploited if the user code is compiled with OpenMP enabled".'''
 
'''"When using sparse matrices, best performance is achied for a row-major sparse matrix format.<br>Moreover, in this case multi-threading can be exploited if the user code is compiled with OpenMP enabled".'''
 +
 +
Eigen uses number of threads specified my OopenMP, unless <code>Eigen::setNbThreads(n);</code> was called.
 +
Minimal working example:
 +
 +
<figure id="fig:eigen_par">
 +
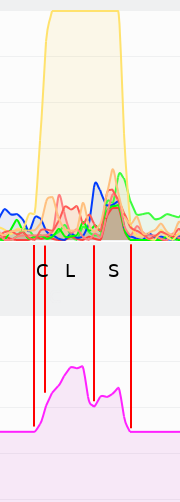
[[File:eigen_parallel_2.png|600px|thumb|upright=2|alt=Matrix of the discretized PDE.|<caption>Matrix of the discretized PDE. </caption>]]
 +
</figure>
 +
 +
<code>
 +
#include <iostream>
 +
#include <vector>
 +
#include "Eigen/Sparse"
 +
#include "Eigen/IterativeLinearSolvers"
 +
 +
using namespace std;
 +
using namespace Eigen;
 +
 +
int main(int argc, char* argv[]) {
 +
 +
    assert(argc == 2 && "Second argument is size of the system.");
 +
    stringstream ss(argv[1]);
 +
    int n;
 +
    ss >> n;
 +
    cout << "n = " << n << endl;
 +
 +
    // Fill the matrix
 +
    VectorXd b = VectorXd::Ones(n) / n / n;
 +
    b(0) = b(n-1) = 1;
 +
    SparseMatrix<double, RowMajor> A(n, n);
 +
    A.reserve(vector<int>(n, 3));  // 3 per row
 +
    for (int i = 0; i < n-1; ++i) {
 +
        A.insert(i, i) = -2;
 +
        A.insert(i, i+1) = 1;
 +
        A.insert(i+1, i) = 1;
 +
    }
 +
    A.coeffRef(0, 0) = 1;
 +
    A.coeffRef(0, 1) = 0;
 +
    A.coeffRef(n-1, n-2) = 0;
 +
    A.coeffRef(n-1, n-1) = 1;
 +
 +
    // Solve the system
 +
    BiCGSTAB<SparseMatrix<double, RowMajor>, IncompleteLUT<double>> solver;
 +
    solver.setTolerance(1e-10);
 +
    solver.setMaxIterations(1000);
 +
    solver.compute(A);
 +
    VectorXd x = solver.solve(b);
 +
    cout << "#iterations:    " << solver.iterations() << endl;
 +
    cout << "estimated error: " << solver.error()      << endl;
 +
    cout << "sol: " << x.head(6).transpose() << endl;
 +
 +
    return 0;
 +
}
 +
</code>
 +
 +
was compiled with <code>g++ -o parallel_solve -O3 -fopenmp solver_test_parallel.cpp</code>
 +
Figure <xr id="fig:eigen_par"/>. was produced when the program above was run as <code>./parallel_solve 10000000</code>.

Revision as of 14:03, 16 March 2017

There are many methods available for solving sparse systems. We compare some of them here.

Matrix of the discretized PDE.
Figure 1: Matrix of the discretized PDE.

Mathematica has the following methods available (https://reference.wolfram.com/language/ref/LinearSolve.html#DetailsAndOptions)

  • direct: banded, cholesky, multifrontal (direct sparse LU)
  • iterative: Krylov

Matlab has the following methods:

Eigen has the following methods: (https://eigen.tuxfamily.org/dox-devel/group__TopicSparseSystems.html)

  • direct: sparse LU
  • iterative: bicgstab, cg

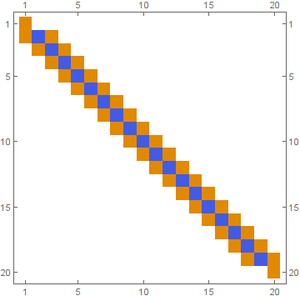
Solving a simple sparse system $A x = b$ for steady space of heat equation in 1d with $n$ nodes, results in a matrix shown in Figure Figure 1.

The following timings of solvers are given in seconds:

$n = 10^6$ Matlab Mathematica Eigen
Banded 0.16 0.28 0.04
SparseLU / 1.73 0.82
BICGStab / Krylov 0.33 0.39 0.53

Incomplete LU preconditioner was used for BICGStab. Without the preconditioner BICGStab does not converge.

BICGStab can be run in parallel, as explain in the general parallelism: https://eigen.tuxfamily.org/dox/TopicMultiThreading.html, and specifically

"When using sparse matrices, best performance is achied for a row-major sparse matrix format.
Moreover, in this case multi-threading can be exploited if the user code is compiled with OpenMP enabled".

Eigen uses number of threads specified my OopenMP, unless Eigen::setNbThreads(n); was called. Minimal working example:

Matrix of the discretized PDE.
Figure 2: Matrix of the discretized PDE.

  1. include <iostream>
  2. include <vector>
  3. include "Eigen/Sparse"
  4. include "Eigen/IterativeLinearSolvers"

using namespace std; using namespace Eigen;

int main(int argc, char* argv[]) { 

   assert(argc == 2 && "Second argument is size of the system.");
   stringstream ss(argv[1]);
   int n;
   ss >> n;
   cout << "n = " << n << endl;

   // Fill the matrix
   VectorXd b = VectorXd::Ones(n) / n / n;
   b(0) = b(n-1) = 1;
   SparseMatrix<double, RowMajor> A(n, n);
   A.reserve(vector<int>(n, 3));  // 3 per row
   for (int i = 0; i < n-1; ++i) {
       A.insert(i, i) = -2;
       A.insert(i, i+1) = 1;
       A.insert(i+1, i) = 1;
   }
   A.coeffRef(0, 0) = 1;
   A.coeffRef(0, 1) = 0;
   A.coeffRef(n-1, n-2) = 0;
   A.coeffRef(n-1, n-1) = 1;

   // Solve the system
   BiCGSTAB<SparseMatrix<double, RowMajor>, IncompleteLUT<double>> solver;
   solver.setTolerance(1e-10);
   solver.setMaxIterations(1000);
   solver.compute(A);
   VectorXd x = solver.solve(b);
   cout << "#iterations:     " << solver.iterations() << endl;
   cout << "estimated error: " << solver.error()      << endl;
   cout << "sol: " << x.head(6).transpose() << endl;

   return 0;

}

was compiled with g++ -o parallel_solve -O3 -fopenmp solver_test_parallel.cpp Figure Figure 2. was produced when the program above was run as ./parallel_solve 10000000.

Retrieved from "http://e6.ijs.si/medusa/wiki/index.php?title=Solving_sparse_systems&oldid=987"