Difference between revisions of "K-d tree"
| Line 1: | Line 1: | ||
In structured meshes, neighborhood relations are implicitly determined by the mapping from the physical to the logical space. | In structured meshes, neighborhood relations are implicitly determined by the mapping from the physical to the logical space. | ||
| − | In unstructured mesh based approaches, support domains can be determined from the mesh topology. However, in meshless methods, the nearest neighboring nodes in $\Omega_S$ are determined with various algorithms and specialized data structures, we use kD Tree. | + | In unstructured mesh based approaches, support domains can be determined from the mesh topology. However, in meshless methods, the nearest neighboring nodes in $\Omega_S$ are determined with various algorithms and specialized data structures, we use kD Tree. |
| + | |||
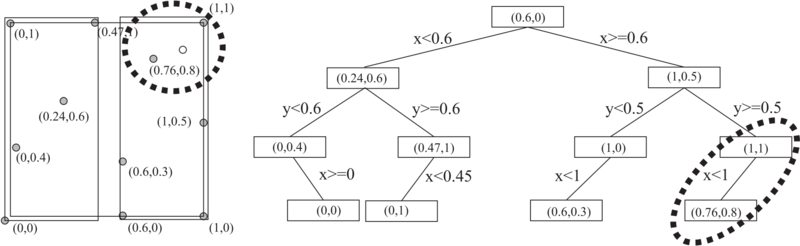
| + | Kd tree is a binary tree which uses hyperplane space partitioning to divide points into subgroups (subtrees). The plane is chosen based on the depth of the tree. At depth $k$, the k-th axis (dimenison) is used to divide remaining points. Example: in 3 dimensions we have x,y and z axes. At root level we decide to divide points according to their $x$ values (we could also do it according to y or z values). Usual criterion for divison of points is median. Thus, at root level we look for median point by looking at x coordiantes of points. We put the median points into the root leaf. Remaining points are put into the left and right subtrees. We put in the left subtree the points which have smaller x coorinate and in the right subtree the points which have larger x coordinate (or vice versa). | ||
The input to Algorithm is a list of $(n_S +1)$ nearest nodes to ${\bf x}$. A naive implementation of finding these nodes could become quite complex if implemented with classical sorting of all nodal distances. Regarding the number of nodes $N$, it approaches the quadratic computational complexity. However, by using efficient data structures, e.g. quadtree, R tree or kD tree (2D tree for 2D domains), the problem becomes tractable. | The input to Algorithm is a list of $(n_S +1)$ nearest nodes to ${\bf x}$. A naive implementation of finding these nodes could become quite complex if implemented with classical sorting of all nodal distances. Regarding the number of nodes $N$, it approaches the quadratic computational complexity. However, by using efficient data structures, e.g. quadtree, R tree or kD tree (2D tree for 2D domains), the problem becomes tractable. | ||
Revision as of 12:47, 15 March 2017
In structured meshes, neighborhood relations are implicitly determined by the mapping from the physical to the logical space. In unstructured mesh based approaches, support domains can be determined from the mesh topology. However, in meshless methods, the nearest neighboring nodes in $\Omega_S$ are determined with various algorithms and specialized data structures, we use kD Tree.
Kd tree is a binary tree which uses hyperplane space partitioning to divide points into subgroups (subtrees). The plane is chosen based on the depth of the tree. At depth $k$, the k-th axis (dimenison) is used to divide remaining points. Example: in 3 dimensions we have x,y and z axes. At root level we decide to divide points according to their $x$ values (we could also do it according to y or z values). Usual criterion for divison of points is median. Thus, at root level we look for median point by looking at x coordiantes of points. We put the median points into the root leaf. Remaining points are put into the left and right subtrees. We put in the left subtree the points which have smaller x coorinate and in the right subtree the points which have larger x coordinate (or vice versa).
The input to Algorithm is a list of $(n_S +1)$ nearest nodes to ${\bf x}$. A naive implementation of finding these nodes could become quite complex if implemented with classical sorting of all nodal distances. Regarding the number of nodes $N$, it approaches the quadratic computational complexity. However, by using efficient data structures, e.g. quadtree, R tree or kD tree (2D tree for 2D domains), the problem becomes tractable. The strategy is to build the data structure only once, before the solution procedure. During the solution, the support nodes of the desired points will then be found much faster.
References
- Trobec R., Kosec G., Šterk M., Šarler B., Comparison of local weak and strong form meshless methods for 2-D diffusion equation. Engineering analysis with boundary elements. 2012;36:310-321;
- Trobec R., Kosec G., Parallel scientific computing : theory, algorithms, and applications of mesh based and meshless methods: Springer; 2015.