Difference between revisions of "1D MLSM and FDM comparison"
(→Neumann case) |
(→Dirichlet case) |
||
| Line 25: | Line 25: | ||
== Dirichlet case == | == Dirichlet case == | ||
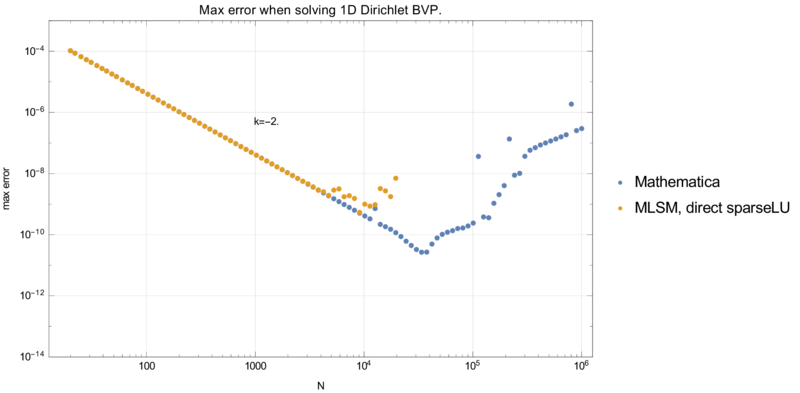
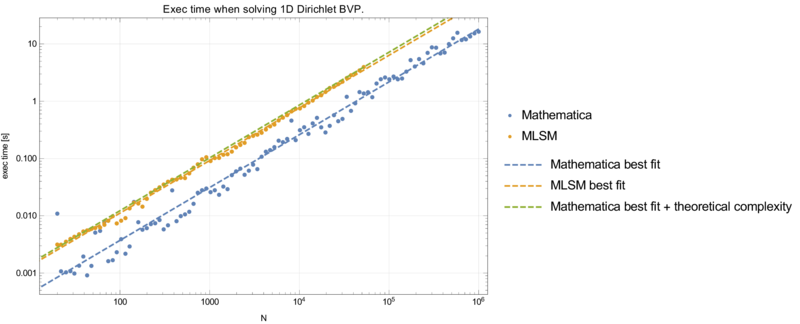
Precision and execution time are summarised in graphs below. | Precision and execution time are summarised in graphs below. | ||
| + | MSLM and Mathematica use $O(nN)$ time to build a matrix and solve the system. Additionally, MLSM uses $O(Nmn^2)$ to construct the shape functions. | ||
| + | The $O$ constant is close to 1 as all operations are basic arithemtic operations. Indded, in this case $n = m = 3$ and if we add this theoretical complexity of $27N$ | ||
| + | to Mathematica case, we fall directly in the MLSM case. | ||
[[File:dircmp.png|800px]][[File:dirtimecmp.png|800px]] | [[File:dircmp.png|800px]][[File:dirtimecmp.png|800px]] | ||
Revision as of 12:11, 13 March 2017
Different numerical approaches to solving a Dirichlet or Neumann problem
\(
\begin{align*}
\text{Dirichlet} && \text{Neumann} \\
f''(x) &= 2x^2+5 \text{ on } (0, 1) & f''(x) &= 2x^2+5 \text{ on } (0, 1) \\
f(0) &= 1 & f'(0) &= 1 \\
f(1) &= 1 & f(1) &= 1 \\
f(x) &= \frac{1}{6} \left(x^4+15 x^2-16 x+6\right) & f(x) &= \frac{1}{6} \left(x^4+15 x^2+6 x-16\right)
\end{align*}
\)
were analysed. Theoretically, FDM and MLSM should match completely. This is practivaly demonstrated up to certain discretization level.
The interval \([0, 1]\) was always discretized uniformly using $N$ nodes, \(x_i = a+i h, h = (b-a)/N\).
Preliminaries
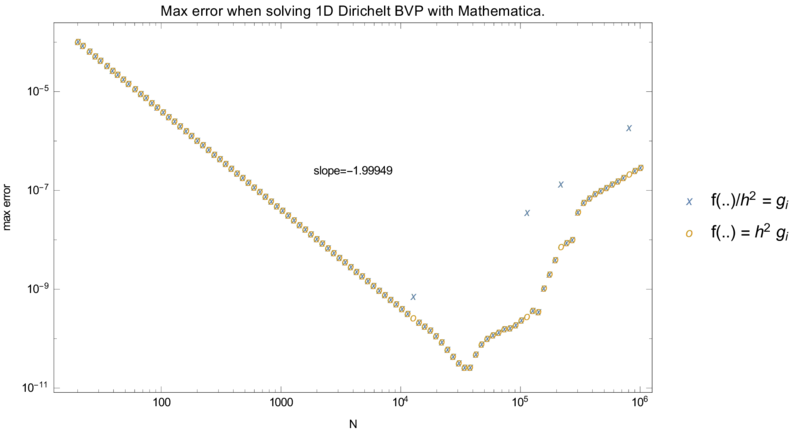
When solving such problems one usually makes the disretization of the form \(f''(x_i) \approx (f_{i-1} -2 f_i + f{i+1}) / h^2\), but when writing the system of equations, it is usually written as $f_{i-1} -2 f_i + f{i+1} = h^2 g(x_i)$. In the general MLSM formulation it is not possible to always do that and therefore we want to know if there are any numerical differences between solving $f_{i-1} -2 f_i + f{i+1} = h^2 g(x_i)$ and $(f_{i-1} -2 f_i + f{i+1})_h^2 = g(x_i)$. No significant differences were noted.
Dirichlet case
Precision and execution time are summarised in graphs below. MSLM and Mathematica use $O(nN)$ time to build a matrix and solve the system. Additionally, MLSM uses $O(Nmn^2)$ to construct the shape functions. The $O$ constant is close to 1 as all operations are basic arithemtic operations. Indded, in this case $n = m = 3$ and if we add this theoretical complexity of $27N$ to Mathematica case, we fall directly in the MLSM case.
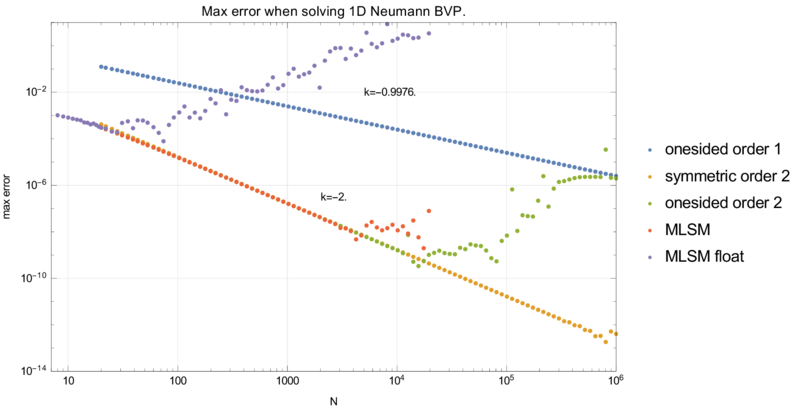
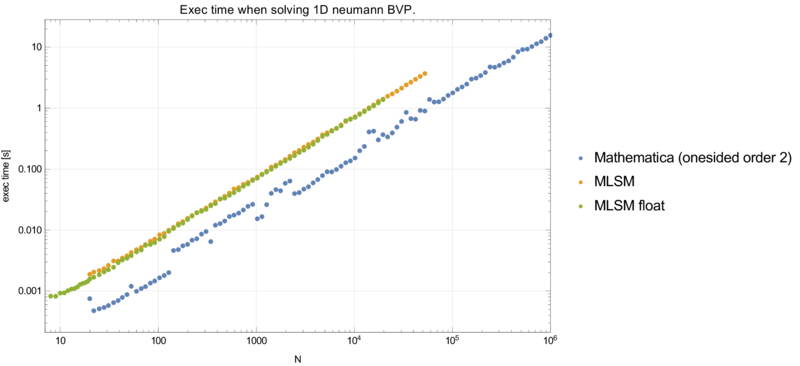
Neumann case
We have more that one possible disctretization of the Neumann BC in point 0. Three explored options are:
- onesided finite difference \(f'(0) \approx (f_1 - f_0) / h\)
- symmetric finite difference \(f'(0) \approx (f_1 - f_{-1}) / h\) and normal discretization in node 0 \(f''(0) \approx (f_1 - 2f_0 + f_{-1}) /h^2\)
- onesided double finite difference \(f'(0) \approx (-3/2 f_0 + 2f_1 -1/2 f_2) / h\)
MLSM with support size $n = 3$ and three polynomial basis functions results in exactly the FDM method with onesided double finite difference approximation.