Difference between revisions of "Point source near an anisotropic lens"
(→Case) |
(→Results) |
||
| Line 50: | Line 50: | ||
==Results== | ==Results== | ||
| − | + | ||
| − | File:FDFD_2D_anizolens_Im.png | + | [[File:FDFD_2D_anizolens_Im.png|800px]] |
| − | File:FDFD_2D_anizolens_Re.png | + | [[File:FDFD_2D_anizolens_Re.png|800px]] |
| − | |||
Revision as of 18:02, 11 August 2020
Back to Computational electromagnetics.
Case
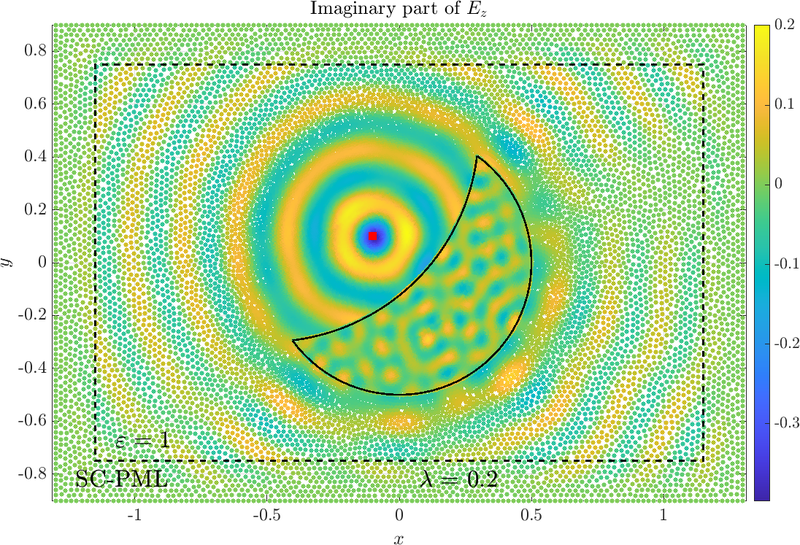
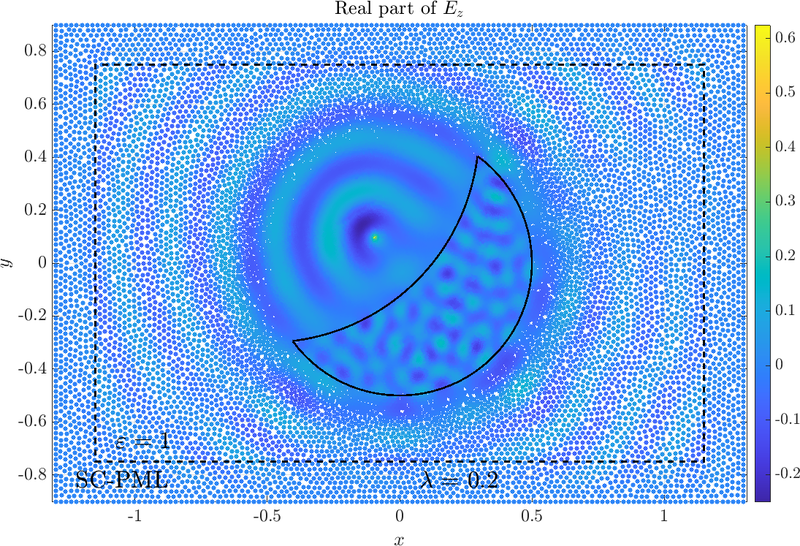
\( \newcommand{\eps}{\varepsilon} \newcommand{\dpar}[2]{\frac{\partial #1}{\partial #2}} \newcommand{\ddpar}[2]{\frac{\partial^2 #1}{\partial #2^2}} \def\doubleunderline#1{\underline{\underline{#1}}}\) Two of the main advantages of meshless methods are accurate discretization of complex surfaces and local refinement of the point distribution. Let us illustrate this on a case where we are simulating the scattering of a point source on an anisotropic lens. The shape of the lens is a difference of two circles with different radii. The lens is made of an anisotropic material its magnetic permeability is thus \begin{equation} \underline{\mu} = \mu_{0} \begin{pmatrix} \mu_{xx} & \mu_{xy} & 0 \\ \mu_{xy} & \mu_{yy} & 0 \\ 0 & 0 & \mu_z \end{pmatrix}, \qquad \eps = \eps_0\eps_r. \end{equation} The dielectric function remains a scalar, this has important consequences for the amplitude equation and the boundary condition between the lens and free space around it. The system of equations we are solving is \begin{align} \nabla \cdot A \nabla v + \mu_z \eps_r \frac{\omega^2}{c_0^2} v = 0 \qquad &\text{in} \quad \Omega \label{eq:anisoInt} \\ \nabla^2 u^s + \frac{\omega^2}{c_0^2} u^s = 0 \qquad &\text{v} \quad \R^2 \setminus \Omega , \label{eq:anisoOut} \end{align} where, \begin{equation} A = \frac{1}{\mu_{xx}\mu_{yy} - \mu_{xy}\mu_{yx}} \begin{pmatrix} \mu_{yy} & -\mu_{yx} \\ -\mu_{xy} & \mu_{xx} \end{pmatrix}. \end{equation} The problem is two-dimensional because of the form of the permeability tensor, the boundary conditions can be derived from Maxwell's equations. As with isotropic materials, the field and its normal derivative have to be continuous on the boundary however, the (anisotropic) normal derivative is defined in a different way \begin{align} v - u^s =u^i \qquad &\text{on} \quad \partial \Omega \label{eq:BC1Aniso} \\ \dpar{v}{n_A\!\!\!} - \dpar{u^s}{n} = \dpar{u^i}{n} \qquad &\text{on} \quad \partial \Omega, \qquad \text{where} \quad \frac{\partial v}{\partial n_A\!\!\!} = n \cdot A \nabla {v}. \label{eq:BC2} \end{align} The incident field results from a point source and is represented by the Green function of the Helmholtz equation in two dimensions \begin{equation} G(r)=\frac{i}{4} H_{0}^{(1)}(kr). \end{equation} The system of equations is easily discretized with the medusa library as both the first term in~\eqref{eq:anisoInt} as well as the derivative $\frac{\partial v}{\partial n_A\!\!\!} $ are only linear combinations of first and second derivatives of the field weighed with the permeability tensor components.
By way of physical intuition, we know we need more points inside and near the lens to better describe the solution. A wave in a dielectric material has a shorter wavelength than in free space and we need more points to resolve it. Around the lens, the scattered field interacts with the incident and we would like to resolve the interference pattern well. The internodal distance is given by \begin{equation} \label{eq:nodaldens} dx(x,y) = \frac{dx_{cyl}-dx_{\Omega}}{1+\left(\frac{r}{a}\right)^p} + dx_{\Omega} \end{equation} Where the parameters $a$ and $p$ control the radius of the refinement and how blurred the edge between the two different nodal densities is.