Difference between revisions of "Computational electromagnetics"
(→Modeling in the time domain) |
|||
| Line 125: | Line 125: | ||
\end{equation} | \end{equation} | ||
==Modeling in the time domain== | ==Modeling in the time domain== | ||
| + | The single most frequent type of calculation used in computational electromagnetics is the simulation of electromagnetic fields in the time domain. The calculation propagates $\b E(\b r, t)$ and $\b H(\b r, t)$ in time, usually starting with all fields set to zero and some time dependent current source $\b J(\b r, t)$. The main advantage of time domain approaches is the ability to study transient phenomena while its main drawback is the study resonant problems. | ||
| + | ===Finite differences in time domain=== | ||
==Modeling in the frequency domain== | ==Modeling in the frequency domain== | ||
==References== | ==References== | ||
Revision as of 03:12, 10 August 2020
Contents
Case studies
The following pages describe the basics of computational electromagnetics, starting with relevant derivations and the basics of classical electromagnetism. The subpages include case studies with analytical solutions if they exist and numerical solutions.
- Triple dielectric step in 1D
- Photonic crystal in 1D
- Scattering from an infinite cylinder
- Point source near an anisotropic lens
Classical electromagnetism
Maxwell's equations in matter
Classical electrodynamics is historically one of the most eminent fields of physics as an extension of classical mechanics, it is very successful in explaining a plethora of phenomena. The dynamics of electric and magnetic fields are described with Maxwell's equations. As we will be studying the interaction of electromagnetic waves with different objects, we need Maxwell's equations in matter \( \newcommand{\dpar}[2]{\frac{\partial #1}{\partial #2}} \begin{align} &\nabla \times \b{E}(\b{r}, t) = - \dpar{\b{B}(\b{r}, t)}{t}, \label{eq:TFaraday} \\ &\nabla \times \b{H}(\b{r}, t) = \b{j}(\b{r}, t) + \dpar{\b{D}(\b{r}, t)}{t}, \label{eq:TMaxwell-Ampere} \\ &\nabla \cdot \b{D}(\b{r}, t) = \rho(\b{r}, t), \label{eq:TGaussE} \\ &\nabla \cdot \b{B}(\b{r}, t) = 0. \label{eq:TGaussM} \end{align} \)
The system of equations contains four fields. The electric field strength $\b E$ and density $\b D$ and the magnetic field strength $\b H$ and density $\b B$. The four fields are accompanied by the current density $\b j$ and the charge density $\rho$. For a full description of electromagnetic phenomena, we need to provide another two constitutive equations, that relate the strength and density of the fields \( \newcommand{\eps}{\varepsilon} \begin{align} \b{B} &= \mu_0 \mu \b{H}, \label{eq:constM} \\ \b{D} &= \eps_0 \eps \b{E} \label{eq:constE} \end{align} \) where $\varepsilon_0$ and $\mu_0$ are vacuum permittivity and permeability respectively. The dielectric function $\varepsilon$ and magnetic permeability $\mu$ are in general dependant on both $\b E$ and $\b B$ as well as the frequency $\omega$ and can be second order tensors in anisotropic materials. Equations \eqref{eq:constM} and \eqref{eq:constE} already assume linear material properties, generally the polarisation $\b P$ and magnetisation are defined as power series expansions of the electric field density and magnetic field density, as \( \begin{align} \label{eq:PMexpans} \b{P} &= \chi_E \b{D} + \mathcal{O}(D^2), \\ \b{M} &= \chi_M \b{H} + \mathcal{O}(H^2). \end{align} \) The material linearity assumption holds well for small external fields, meaning small $\b D$ and $\b H$. The treatment of nonlinear terms falls within the field of nonlinear optics and is not relevant for our discussion here.
Electromagnetic waves
\( \def\doubleunderline#1{\underline{\underline{#1}}} \newcommand{\dpar}[2]{\frac{\partial #1}{\partial #2}} \newcommand{\ddpar}[2]{\frac{\partial^2 #1}{\partial #2^2}} \newcommand{\eps}{\varepsilon} \) When studying light and related phenomena, we are usually interested in the behavior of electromagnetic waves, where the electric and magnetic fields oscillate with constant frequency and propagate in a single direction. The wave formulation helps with understanding optical phenomena such as diffraction and reflection and offers easily graspable quantities such as wave amplitude and wavelength. Wave equations for $\b E$ and $\b H$ can be derived from Maxwell's equations for linear and homogeneous materials. Let's start by treating a more general case, where $\doubleunderline \varepsilon$ is a constant second-order tensor and $\mu$ is a scalar quantity. From Maxwell's equations and constitutive relations we obtain \begin{equation} \nabla \times \left[ \doubleunderline{\varepsilon}^{-1} \nabla \times \b{H} \right] = \nabla \times \left[ \doubleunderline{\varepsilon}^{-1} \b j \right] - \mu \mu_0 \varepsilon_0 \ddpar{\b H}{t}. \end{equation} and \begin{equation} \nabla \times \nabla \times \b{E} = \nabla (\nabla \cdot \b E) - \nabla^2 \b E = -\mu\mu_0\dpar{\b j}{t} - \eps_0 \doubleunderline{\varepsilon} \mu \mu_0 \ddpar{\b E}{t} \end{equation} which simplify to wave equations for homogenous (linear) materials and no external currents and charges \begin{equation} \nabla^2 \b E = \eps\eps_0\mu\mu_0\ddpar{\b E}{t}, \qquad \text{ or } \qquad \nabla^2 \b H = \eps\eps_0\mu\mu_0\ddpar{\b H}{t}. \end{equation} One possible way of solving electromagnetic problems is simply to solve the above wave equations numerically. Another approach is to solve Maxwell's equations in the frequency domain. We start by Fourier expansion of the fields $\b E$, $\b D$, $\b B$ and $\b H$ analogous to \begin{equation} \label{eq:Fdecomp} \b{E}(\b{r}, t) = \int\frac{d\omega}{2\pi} \b{E}(\b{r}, \omega) e^{-i\omega t}, \end{equation} in the frequency domainall the fields become complex. The ratio between the real and complex component of the fields is the phase difference of the material response to external fields. The Fourier expansion leads to the harmonic form of Maxwell's equations \begin{equation} \label{eq:FFaraday} \nabla \times \b{E}(\b{r}, \omega) = - i\omega \b{B} (\b{r}, \omega), \end{equation} \begin{equation} \label{eq:FMaxwell-Ampere} \nabla \times \b{H}(\b{r}, \omega) = i\omega \b{D}(\b{r}, \omega). \end{equation} The constitutive relations are unchanged. If we assume that there are currents we obtain a wave equation for either $\b D$ or $\b H$, \begin{equation} \label{eq:frekaniwave} \nabla \times \left[ \doubleunderline{\eps}^{-1} \nabla \times \b{H} \right] = \omega^2 \mu_0 \eps_0 \mu \b{H}. \end{equation} The above form allows for a calculation of a steady state response to an incident harmonic plane wave, meaning that we can study scattering of any incident wave that can be represented by a plane wave expansion. The time dependent solution is obtained by an inverse Fourier transform. In empty space \eqref{eq:frekaniwave} simplifies to the Helmholtz equation \begin{equation} \label{eq:frekemptywave} \nabla^2 \b{H} = - \omega^2 \mu_0 \eps_0 \b{H} = - k^2 \b{H}. \end{equation} Wavenumber $k$ in a vacuum is defined as $k = \omega \sqrt{\mu_0 \epsilon_0} = \frac{2 \pi}{\lambda}$. One of the major advantages of the frequency domain approach over the time domain approach is that the frequency dependence of the dielectric function does not need to be considered, as one simply uses the value of the dielectric function at a certain frequency.
Boundary conditions for Maxwell's equations
For modeling purposes the treatment of electromagnetic fields on boundaries between materials with different properties, such as $\varepsilon$ and $\mu$, is crucial. The boundary conditions for Maxwell's equations between two linear and homogenous mediums are as follows \begin{equation} \begin{array}{rl} D_{1 n}-D_{2 n}=\sigma, \qquad & E_{1 t}-E_{2 t}=0 \\ B_{1 n}-B_{2 n}=0, \qquad & H_{1 t}-H_{2 t}=K.\end{array} \end{equation} Where we have fields $\b{E}_1, \b{D}_1, \b{B}_1, \b{H}_1$ in medium $1$ and fields $\b{E}_2, \b{D}_2, \b{B}_2, \b{H}_2$ in medium $2$. Subscript $t$ and $n$ denote the tangential and normal component respectively, $\sigma$ is the surface charge density and $\b K$ is the surface current density.
Frequency dependence of the dielectric function
As mentioned above the dielectric function $\varepsilon$ is a function of frequency. Some analytical properties of the dielectric function $\varepsilon(\omega)$ are well known, due to their relevance in optics, one example being the Kramers-Kronig relations. The dielectric function is in general, based on a nonlocal response function $\chi$, defined as \begin{equation} \varepsilon(\omega) = 1 + \int_{0}^{\infty} \chi(\tau) e^{i \omega \tau} \text{d}\tau. \end{equation} For a more detailed analysis of the analytical properties of the function, refer to any standard optics or advanced electromagnetics textbook. When it comes to numerical simulations, models of the dielectric function are of more interest than its analytical properties.
Dielectric materials
The simplest model for dielectrics is based on the equation of motion for the bound charges
\begin{equation}
m \frac{\mathrm{d}^{2} \mathbf{r}}{\mathrm{d} t^{2}}=-m \gamma \dot{\mathbf{r}}-m \omega_{0}^{2} \mathbf{r}+e \mathbf{E}(t)
\end{equation}
the terms on the right side describe the dissipation of energy, oscillations and the driving force of the external electric field. A short calculation leads to an expression of the frequency dependence of the dielectric function
\begin{equation}
\varepsilon(\omega)=1+ \frac{\omega_p}{\left(\omega_{0}^{2}-\omega^{2}\right)-i \gamma \omega}.
\end{equation}
The above expression can be simplified for high and low frequencies leading to the so-called Debye and Plasmonic relaxation models. The Lorentz model applies for frequencies where no terms in the denominator can be neglected. Typical Debye and Lorentz relaxations are shown in the plots below.
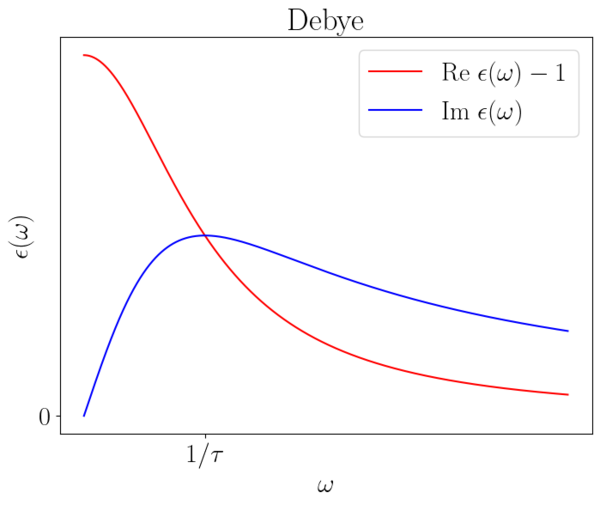
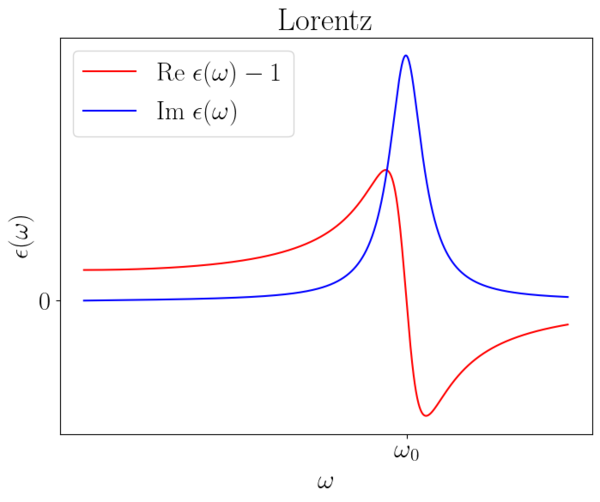
In general, the dielectric function of a material is modeled as a sum of many Debye and Lorentz relaxations, the parameters of which are determined by microscopic properties of the material itself, an extremely interesting case study is the dielectric function of water.
Conductors
When dealing with conductors we use the Drude model of conduction \begin{equation} m \frac{d \mathbf{v}(t)}{d t}=-m \gamma \mathbf{v}(t)+e \mathbf{E}(t) \end{equation} from which we quickly derive the equation for conductivity \begin{equation} \sigma(\omega)=\frac{n e^{2}}{m} \frac{1}{\gamma-i \omega}, \end{equation} which we can relate to the dielectric function \begin{equation} \varepsilon(\omega)=1-\frac{\sigma(\omega)}{i \varepsilon_{0} \omega}. \end{equation}
Modeling in the time domain
The single most frequent type of calculation used in computational electromagnetics is the simulation of electromagnetic fields in the time domain. The calculation propagates $\b E(\b r, t)$ and $\b H(\b r, t)$ in time, usually starting with all fields set to zero and some time dependent current source $\b J(\b r, t)$. The main advantage of time domain approaches is the ability to study transient phenomena while its main drawback is the study resonant problems.