Difference between revisions of "Natural convection in 3D irregular domain"
| Line 1: | Line 1: | ||
| − | The classical [[De Vahl Davis natural convection test]] can be extended to 3D | + | The classical [[De Vahl Davis natural convection test]] can be extended to 3D [] |
| + | |||
| + | |||
All spatial operators are discretized using RBF-FD with $r^3$ PHS radial basis | All spatial operators are discretized using RBF-FD with $r^3$ PHS radial basis | ||
functions, augmented with monomials up to order $2$, with the closest $25$ | functions, augmented with monomials up to order $2$, with the closest $25$ | ||
| Line 8: | Line 10: | ||
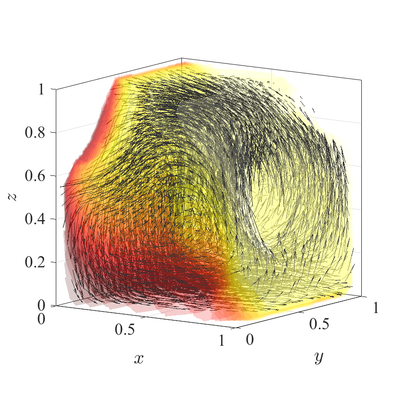
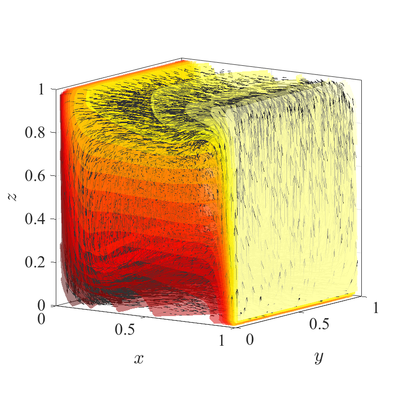
[[File:DVD_3D_irreg.png|400px]][[File:DVD_3D.png|400px]] | [[File:DVD_3D_irreg.png|400px]][[File:DVD_3D.png|400px]] | ||
| + | |||
| + | |||
| + | \begin{table}[h] | ||
| + | \centering | ||
| + | \caption{Comparison of results computed with RBF-FD on FF nodes and reference | ||
| + | data. } | ||
| + | \label{tab:ff-data} | ||
| + | \renewcommand{\arraystretch}{1.2} | ||
| + | \scalebox{0.68}{ | ||
| + | \begin{tabular}{|l|l|l|l|l|l|l|l|l|l|l|l|l|l|} | ||
| + | \cline{2-14} | ||
| + | \multicolumn{1}{c|}{} & \multirow{2}{*}{\textbf{Ra}} & | ||
| + | \multicolumn{3}{c|}{$v_{max}(x, 0.5)$} & \multicolumn{3}{c|}{$x$} & | ||
| + | \multicolumn{3}{c|}{$u_{max}(0.5, y)$} & \multicolumn{3}{c|}{$y$} | ||
| + | \\ \cline{3-14} | ||
| + | \multicolumn{1}{c|}{} & \multicolumn{1}{c|}{} & present & | ||
| + | \multicolumn{1}{c|}{\cite{couturier2000performance}} & | ||
| + | \multicolumn{1}{c|}{\cite{kosec2008solution}} & present & | ||
| + | \multicolumn{1}{c|}{\cite{couturier2000performance}} & | ||
| + | \multicolumn{1}{c|}{\cite{kosec2008solution}} & present & | ||
| + | \multicolumn{1}{c|}{\cite{couturier2000performance}} & | ||
| + | \multicolumn{1}{c|}{\cite{kosec2008solution}} & present & | ||
| + | \multicolumn{1}{c|}{\cite{couturier2000performance}} & | ||
| + | \multicolumn{1}{c|}{\cite{kosec2008solution}} | ||
| + | \\ \hline \hline | ||
| + | \multirow{3}{*}{\textbf{2D}} & $10^6$ & 0.2628 & 0.2604 & | ||
| + | 0.2627 & 0.037 & 0.038 & 0.039 & 0.0781 & 0.0765 & 0.0782 & 0.847 | ||
| + | & 0.851 & 0.861 | ||
| + | \\ \cline{2-14} | ||
| + | & $10^7$ & 0.2633 & 0.2580 & 0.2579 & 0.022 & 0.023 & 0.021 & 0.0588 | ||
| + | & 0.0547 & 0.0561 & 0.870 & 0.888 & 0.900 | ||
| + | \\ \cline{2-14} | ||
| + | & $10^8$ & 0.2557 & 0.2587 & 0.2487 & 0.010 & 0.011 & 0.009 & 0.0314 | ||
| + | & 0.0379 & 0.0331 & 0.918 & 0.943 & 0.930 | ||
| + | \\ \hline \hline | ||
| + | \multicolumn{1}{c|}{} & \multirow{2}{*}{\textbf{Ra}} & | ||
| + | \multicolumn{3}{c|}{$w_{max}(x, 0.5,0.5)$} & \multicolumn{3}{c|}{$x$} & | ||
| + | \multicolumn{3}{c|}{$u_{max}(0.5, 0.5, z)$} & \multicolumn{3}{c|}{$z$} | ||
| + | \\ \cline{3-14} | ||
| + | \multicolumn{1}{c|}{} & \multicolumn{1}{c|}{} & present & | ||
| + | \multicolumn{1}{c|}{\cite{wang2017numerical}} | ||
| + | & \multicolumn{1}{c|}{\cite{fusegi1991numerical}} & present & | ||
| + | \multicolumn{1}{c|}{\cite{wang2017numerical}} | ||
| + | & \multicolumn{1}{c|}{\cite{fusegi1991numerical}} & present & | ||
| + | \multicolumn{1}{c|}{\cite{wang2017numerical}} | ||
| + | & \multicolumn{1}{c|}{\cite{fusegi1991numerical}} & present & | ||
| + | \multicolumn{1}{c|}{\cite{wang2017numerical}} & | ||
| + | \multicolumn{1}{c|}{\cite{fusegi1991numerical}} | ||
| + | \\ \hline | ||
| + | \multirow{3}{*}{\textbf{3D}} & $10^4$ & 0.2295 & 0.2218 & 0.2252 & 0.850 & 0.887 & 0.883 | ||
| + | & 0.2135 & 0.1968 & 0.2013 & 0.168 & 0.179 & 0.183 \\ \cline{2-14} | ||
| + | & $10^5$ & 0.2545 & 0.2442 & 0.2471 & 0.940 & 0.931 & 0.935 & 0.1564 & 0.1426 & 0.1468 | ||
| + | & 0.144 & 0.149 & 0.145 | ||
| + | \\ \cline{2-14} | ||
| + | & $10^6$ & 0.2564 & 0.2556 & 0.2588 & 0.961 & 0.965 & 0.966 & 0.0841 | ||
| + | & 0.0816 & 0.0841 & 0.143 & 0.140 & 0.144 | ||
| + | \\ \hline | ||
| + | \end{tabular} | ||
| + | } | ||
| + | \end{table} | ||
Revision as of 15:22, 18 May 2019
The classical De Vahl Davis natural convection test can be extended to 3D []
All spatial operators are discretized using RBF-FD with $r^3$ PHS radial basis
functions, augmented with monomials up to order $2$, with the closest $25$
nodes used as a stencil. For the time discretization time step
$\Delta t=10^{-3}$ was used for all cases. Nodal distance $h=0.01$ is used for
simulations in 2D and $h=0.25$ for simulations in 3D. Boundaries with Neumann
boundary conditions are additionally treated with ghost nodes Ghost nodes (theory).
\begin{table}[h]
\centering
\caption{Comparison of results computed with RBF-FD on FF nodes and reference
data. }
\label{tab:ff-data}
\renewcommand{\arraystretch}{1.2}
\scalebox{0.68}{
\begin{tabular}{|l|l|l|l|l|l|l|l|l|l|l|l|l|l|}
\cline{2-14}
\multicolumn{1}{c|}{} & \multirow{2}{*}{\textbf{Ra}} &
\multicolumn{3}{c|}{$v_{max}(x, 0.5)'"`UNIQ-MathJax7-QINU`"'x'"`UNIQ-MathJax8-QINU`"'u_{max}(0.5, y)'"`UNIQ-MathJax9-QINU`"'y'"`UNIQ-MathJax10-QINU`"'10^6'"`UNIQ-MathJax11-QINU`"'10^7'"`UNIQ-MathJax12-QINU`"'10^8'"`UNIQ-MathJax13-QINU`"'w_{max}(x, 0.5,0.5)'"`UNIQ-MathJax14-QINU`"'x'"`UNIQ-MathJax15-QINU`"'u_{max}(0.5, 0.5, z)'"`UNIQ-MathJax16-QINU`"'z'"`UNIQ-MathJax17-QINU`"'10^4'"`UNIQ-MathJax18-QINU`"'10^5'"`UNIQ-MathJax19-QINU`"'10^6$ & 0.2564 & 0.2556 & 0.2588 & 0.961 & 0.965 & 0.966 & 0.0841
& 0.0816 & 0.0841 & 0.143 & 0.140 & 0.144
\\ \hline
\end{tabular}
}
\end{table}