Difference between revisions of "Positioning of computational nodes"
(→Filling domain with nodes) |
(→Filling domain with nodes) |
||
| Line 13: | Line 13: | ||
Examples of PDS discretized irregular domains in 2D (first code snippet, left image) and in 3D (second code snipper, right image) can be found below. | Examples of PDS discretized irregular domains in 2D (first code snippet, left image) and in 3D (second code snipper, right image) can be found below. | ||
<syntaxhighlight lang="c++" line> | <syntaxhighlight lang="c++" line> | ||
| + | // setup | ||
PoissonDiskSamplingFill fill_engine; | PoissonDiskSamplingFill fill_engine; | ||
| − | |||
fill_engine.iterations(1000000).optim_after(1000).use_MC(true).proximity_relax(0.8); | fill_engine.iterations(1000000).optim_after(1000).use_MC(true).proximity_relax(0.8); | ||
// create test domain | // create test domain | ||
| Line 29: | Line 29: | ||
<syntaxhighlight lang="c++" line> | <syntaxhighlight lang="c++" line> | ||
PoissonDiskSamplingFill fill_engine; | PoissonDiskSamplingFill fill_engine; | ||
| + | // setup | ||
PoissonDiskSamplingFill fill_engine; | PoissonDiskSamplingFill fill_engine; | ||
| − | |||
fill_engine.iterations(1000000).optim_after(1000).use_MC(true).proximity_relax(0.8); | fill_engine.iterations(1000000).optim_after(1000).use_MC(true).proximity_relax(0.8); | ||
// create test domain | // create test domain | ||
Revision as of 21:15, 15 January 2018
Although the meshless methods do not require any topological relations between nodes and even randomly distributed nodes could be used, it is well-known that using regularly distributed nodes leads to more accurate and more stable results. So despite meshless seeming robustness regarding the nodal distribution, a certain effort has to be invested into the positioning of the nodes and following discussion, to some extent, deals with this problem. In a following discussion we want to form set of algorithms that can cover arbitrary domain in n dimensions with nodes that can be further used to solve systems of PDEs. We start with algorithms for filling the domain with nodes. Second set is denoted to improving the nodal distributions and a last set of algorithms deals with the refinement of the nodal distribution. The algorithms can of course be combined.
Filling domain with nodes
The goal is to fill arbitrary domain, which we can ask if position $\b{p}$ is in the domain our outside, with nodes following the given target density function $\rho(\b{p})$.
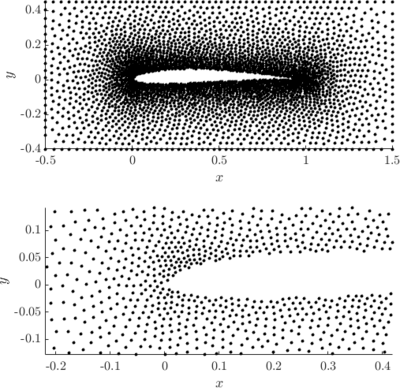
We start with a simple algorithm based on Poisson Disk Sampling (PDS) that results in a relatively tightly packed distribution of nodes. What we do is:
- Randomly select a node within the domain.
- Add N (depending on the dimensionality of the space) on circle/sphere around that node.
- Randomly select one of just added nodes and repeat adding.
- Each time check if any of new nodes violates minimal distance criterion, i.e. if it is positioned to close to any of the existing nodes.
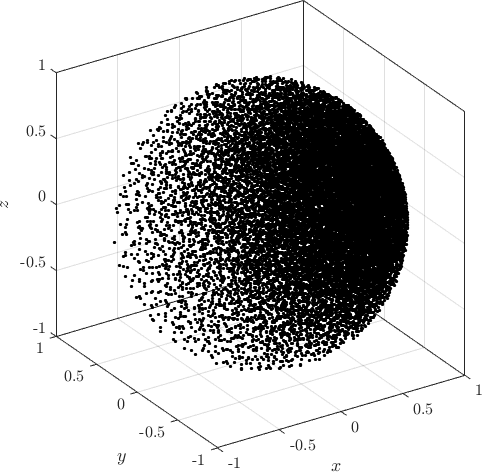
Examples of PDS discretized irregular domains in 2D (first code snippet, left image) and in 3D (second code snipper, right image) can be found below.
1 // setup
2 PoissonDiskSamplingFill fill_engine;
3 fill_engine.iterations(1000000).optim_after(1000).use_MC(true).proximity_relax(0.8);
4 // create test domain
5 RectangleDomain<Vec2d> domain({0, 0}, {1.2, 1.5});
6 CircleDomain<Vec2d> o1({0.4, 0.4}, 0.25);
7 domain.subtract(o1);
8 // define density function
9 auto fill_density = [](Vec2d p)->double{
10 return (std::pow(p[0]/10, 2) + 0.01);
11 };
12 fill_engine(domain, fill_density);
1 PoissonDiskSamplingFill fill_engine;
2 // setup
3 PoissonDiskSamplingFill fill_engine;
4 fill_engine.iterations(1000000).optim_after(1000).use_MC(true).proximity_relax(0.8);
5 // create test domain
6 RectangleDomain<Vec3d> domain({0, 0, 0}, {1.2, 1.5, 1.1});
7 CircleDomain<Vec3d> o1({0, 0, 0}, 0.5);
8 domain.subtract(o1);
9 // define target density
10 auto fill_density = [](Vec3d p)->double{
11 return (std::pow(p[0]/10 + p[1]/10 + p[2]/10, 2) + 0.025);
12 };
13 fill_engine(domain, fill_density);