Difference between revisions of "Meshless Local Strong Form Method (MLSM)"
| Line 2: | Line 2: | ||
<figure id="fig:square_heat"> | <figure id="fig:square_heat"> | ||
| − | [[File:image_1avhoje8u10tg1cip1atj1qo51j8b9.png| | + | [[File:image_1avhoje8u10tg1cip1atj1qo51j8b9.png|600px|thumb|upright=2|alt=The scheme of local meshless principle.|<caption>The scheme of local meshless principle. </caption>]] |
</figure> | </figure> | ||
The elegance of MLSM is its simplicity and generality. The presented methodology can be also easily upgraded or altered, e.g. with nodal adaptation, basis augmentation, conditioning of the approximation, etc., to treat anomalies such as sharp discontinues or other obscure situations, which might occur in complex simulations. In the MLSM, the type of approximation, the size of support domain, and the type and number of basis function is general. For example minimal support size for 2D transport problem (system of PDEs of second order) is five, however higher support domains can be used to stabilize computations on scattered nodes at the cost of computational complexity. Various types of basis functions might appear in the calculation of the trial function, however, the most commonly used are multiquadrics, Gaussians and monomials. Some authors also enrich the radial basis with monomials to improve performance of the method. All these features can be controlled on the fly during the simulation. From the computation point of view, the localization of the method reduces inter-processor communication, which is often a bottleneck of parallel algorithms. | The elegance of MLSM is its simplicity and generality. The presented methodology can be also easily upgraded or altered, e.g. with nodal adaptation, basis augmentation, conditioning of the approximation, etc., to treat anomalies such as sharp discontinues or other obscure situations, which might occur in complex simulations. In the MLSM, the type of approximation, the size of support domain, and the type and number of basis function is general. For example minimal support size for 2D transport problem (system of PDEs of second order) is five, however higher support domains can be used to stabilize computations on scattered nodes at the cost of computational complexity. Various types of basis functions might appear in the calculation of the trial function, however, the most commonly used are multiquadrics, Gaussians and monomials. Some authors also enrich the radial basis with monomials to improve performance of the method. All these features can be controlled on the fly during the simulation. From the computation point of view, the localization of the method reduces inter-processor communication, which is often a bottleneck of parallel algorithms. | ||
Revision as of 20:34, 20 October 2016
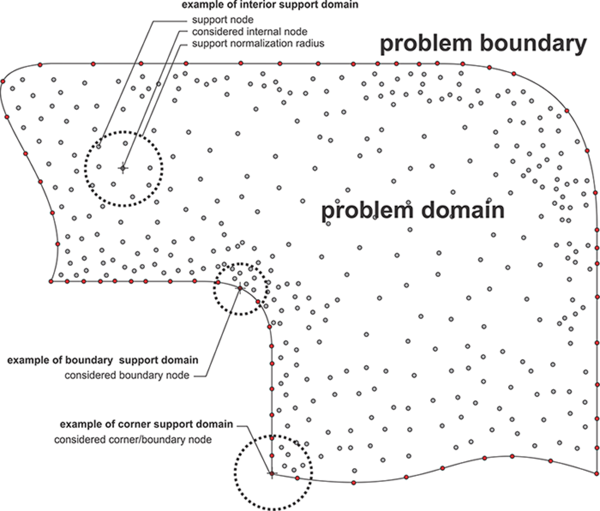
The Meshless Local Strong Form Method (MLSM) is a generalization of methods which are in literature also known as Diffuse Approximate Method (DAM), Local Radial Basis Function Collocation Methods (LRBFCM), Generalized FDM, Collocated discrete least squares (CDLS) meshless, etc. Although each of the named methods pose some unique properties, the basic concept of all local strong form methods is similar, namely to approximate treated fields with nodal trial functions over the local support domain. The nodal trial function is then used to evaluate various operators, e.g. derivation, integration, and after all, approximation of a considered field in arbitrary position. The MLSM could easily be understood as a meshless generalization of the FDM, however much more powerful. MLSM has an ambition to avoid using pre-defined relations between nodes and shift this task into the solution procedure. The final goal of such an approach is higher flexibility in complex domains.
The elegance of MLSM is its simplicity and generality. The presented methodology can be also easily upgraded or altered, e.g. with nodal adaptation, basis augmentation, conditioning of the approximation, etc., to treat anomalies such as sharp discontinues or other obscure situations, which might occur in complex simulations. In the MLSM, the type of approximation, the size of support domain, and the type and number of basis function is general. For example minimal support size for 2D transport problem (system of PDEs of second order) is five, however higher support domains can be used to stabilize computations on scattered nodes at the cost of computational complexity. Various types of basis functions might appear in the calculation of the trial function, however, the most commonly used are multiquadrics, Gaussians and monomials. Some authors also enrich the radial basis with monomials to improve performance of the method. All these features can be controlled on the fly during the simulation. From the computation point of view, the localization of the method reduces inter-processor communication, which is often a bottleneck of parallel algorithms.