Difference between revisions of "K-d tree"

Revision as of 21:09, 22 May 2017

In structured meshes, neighborhood relations are implicitly determined by the mapping from the physical to the logical space. In unstructured mesh based approaches, support domains can be determined from the mesh topology. However, in meshless methods, the nearest neighboring nodes in $\Omega_S$ are determined with various algorithms and specialized data structures, we use kD Tree.

The input to Algorithm is a list of $(n_S +1)$ nearest nodes to ${\bf x}$. A naive implementation of finding these nodes could become quite complex if implemented with classical sorting of all nodal distances. Regarding the number of nodes $N$, it approaches the quadratic computational complexity. However, by using efficient data structures, e.g. quadtree, R tree or kD tree (2D tree for 2D domains), the problem becomes tractable. The strategy is to build the data structure only once, before the solution procedure. During the solution, the support nodes of the desired points will then be found much faster.

2D tree example

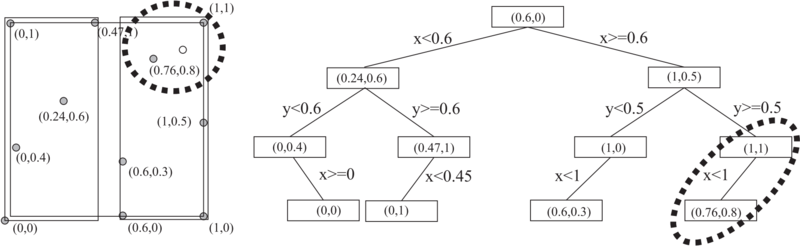
Kd tree is a binary tree which uses hyperplane space partitioning to divide points into subgroups (subtrees). The plane is chosen based on the depth of the node in a tree. At depth $k$, the k-th axis (dimenison) is used to divide the remaining points. Example: in 3 dimensions we have x,y and z axes. At root level we decide to divide points according to their $x$ values (we could also do it according to y or z values). Usual criterion for divison of points is median. Thus, at root level, we look for median point by looking at x coordiantes of all points. We put the median point into the root leaf. Remaining points are put into the left and right subtrees. We put the points which have smaller x coorinate into the left subtree and points which have larger x coorinate into the right subtree (or vice versa). We construct the two children nodes of the root from the two subgroups we just created. The procedure is the same, except that we divide the space according to y or z coordinate. We continue this way until we run out of points. The axes used for median search are periodically repeating.

The procedure described above is used to construct a tree from a collection of given points and is used by ANN library. The tree can also be constructed by inserting points one by one. Such procedure is used by Libssrckdtree library. Time complexity of both procedures is $o(nlogn)$. The most time consuming part of the former algorithm is median point selection. It's time complexity is o(n). This can be improved by imploying some smarter schemes than median finding (consult literature). Time complexity of the second algorithm can quickly be calculated from the average time need to insert a node into the tree - it scales o($log n$). Inserting n nodes thus again results in $n log n$ time complexity.

We tested build times for Ann and Libssrckdtree libraries. We also included a cover tree library, which can be found here.

File:Tree building time.jpg

Nearest neighbor search is a $log n$ procedure, although in practice, especially in higher dimensions, it's closer to o(n). There is a nice description of the algorithm on wikipedia website. We tested ANN and Libssrckdtree implementations. In addition we tested also cover tree nearest neighbor search.

800px

Note that cover tree implementation is not the best available, but it is the only one to have insert/remove and is written in c++.

References

• Trobec R., Kosec G., Šterk M., Šarler B., Comparison of local weak and strong form meshless methods for 2-D diffusion equation. Engineering analysis with boundary elements. 2012;36:310-321;
• Trobec R., Kosec G., Parallel scientific computing : theory, algorithms, and applications of mesh based and meshless methods: Springer; 2015.
• k-d tree. (n.d.). In Wikipedia. Retrieved March 17, 2017, from https://en.wikipedia.org/wiki/K-d_tree