Difference between revisions of "Solving sparse systems"
| Line 43: | Line 43: | ||
Incomplete LU preconditioner was used for BICGStab. | Incomplete LU preconditioner was used for BICGStab. | ||
Without the preconditioner BICGStab does not converge. | Without the preconditioner BICGStab does not converge. | ||
| + | |||
| + | BICGStab can be run in parallel, as explain in the general parallelism: https://eigen.tuxfamily.org/dox/TopicMultiThreading.html, and specifically | ||
| + | "When using sparse matrices, best performance is achied for a row-major sparse matrix format. Moreover, in this case multi-threading can be exploited if the user code is compiled with OpenMP enabled". | ||
Revision as of 13:33, 16 March 2017
There are many methods available for solving sparse systems. We compare some of them here.
Mathematica has the following methods available (https://reference.wolfram.com/language/ref/LinearSolve.html#DetailsAndOptions)
- direct: banded, cholesky, multifrontal (direct sparse LU)
- iterative: Krylov
Matlab has the following methods:
- direct: https://www.mathworks.com/help/matlab/ref/mldivide.html#bt42omx_head
- iterative: https://www.mathworks.com/help/matlab/math/systems-of-linear-equations.html#brzoiix, including bicgstab, gmres
Eigen has the following methods: (https://eigen.tuxfamily.org/dox-devel/group__TopicSparseSystems.html)
- direct: sparse LU
- iterative: bicgstab, cg
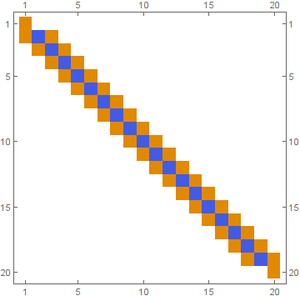
Solving a simple sparse system $A x = b$ for steady space of heat equation in 1d with $n$ nodes, results in a matrix shown in Figure Figure 1.
The following timings of solvers are given in seconds:
| $n = 10^6$ | Matlab | Mathematica | Eigen |
|---|---|---|---|
| Banded | 0.16 | 0.28 | 0.04 |
| SparseLU | / | 1.73 | 0.82 |
| BICGStab / Krylov | 0.33 | 0.39 | 0.53 |
Incomplete LU preconditioner was used for BICGStab. Without the preconditioner BICGStab does not converge.
BICGStab can be run in parallel, as explain in the general parallelism: https://eigen.tuxfamily.org/dox/TopicMultiThreading.html, and specifically "When using sparse matrices, best performance is achied for a row-major sparse matrix format. Moreover, in this case multi-threading can be exploited if the user code is compiled with OpenMP enabled".