Difference between revisions of "Analysis of MLSM performance"
| Line 84: | Line 84: | ||
==Solving Dirichlet with EngineMLS== | ==Solving Dirichlet with EngineMLS== | ||
| − | Example code using explicit stepping to reproduce the thermal images from the beginning: | + | Example code using explicit stepping to reproduce the thermal images from the beginning: [https://gitlab.com/e62Lab/e62numcodes/blob/master/examples/diffusion/diffusion.cpp example code] |
| + | |||
| + | ==Solving Dirichlet with MLSM operators== | ||
| + | Example code using explicit stepping and MLSM operators to reproduce the thermal images from the beginning:[https://gitlab.com/e62Lab/e62numcodes/blob/master/examples/diffusion/diffusion_mlsm_operators.cpp example code] | ||
| + | |||
| + | ==Solving mixed boundary conditions with MLSM operators== | ||
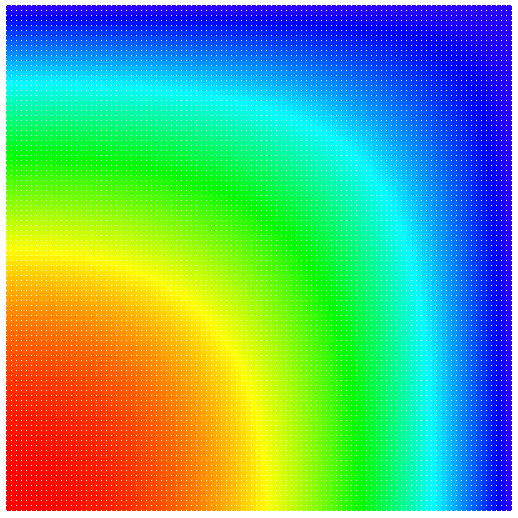
| + | By using MLSM operators and utilizing its `MLSM::neumann` method we can also solve | ||
| + | partial diffusion equations. | ||
| + | |||
| + | [[File:quarter_diffusion.png|600px|center]] | ||
| + | |||
| + | Example code showing the use of Neumann boundary conditions:[] | ||
| + | |||
| + | @snippet mlsm_operators_test.cpp Quarter diffusion example | ||
| + | |||
| + | We also support more – interesting – domains :) | ||
| + | |||
| + | @image html mikimouse_heat.png | ||
| + | @image latex mikimouse_heat.png | ||
Revision as of 14:38, 20 October 2016
For starters, we can solve simple Diffusion equation $ \nabla^2 u = \frac{\partial u}{\partial t} $.
We solved the equation on a square $\Omega = [0, a] \times [0, a]$ with Dirichlet boundary conditions $ \left. u\right|_{\partial \Omega} = 0 $ and initial state $ u(t = 0) = 1$.
An analytical solution for this domain is known, and we use it to evaluate or own solution. \begin{equation} u(\vec{p}, t) = \sum_{\substack{n=1 \\ n \text{ odd}}}^\infty\sum_{\substack{m=1 \\ m \text{ odd}}}^\infty \frac{1}{\pi^2} \frac{16 a^2}{nm} \sin\left(\frac{\pi n}{a}p_x\right) \sin\left(\frac{\pi m}{a}p_y\right) e^{-\frac{\pi^2 (n^2+m^2)}{a^2}t} \end{equation} Because the solution is given in the series form, we only compare to the finite approximation, summing to $N = 100$ instead of infinity.
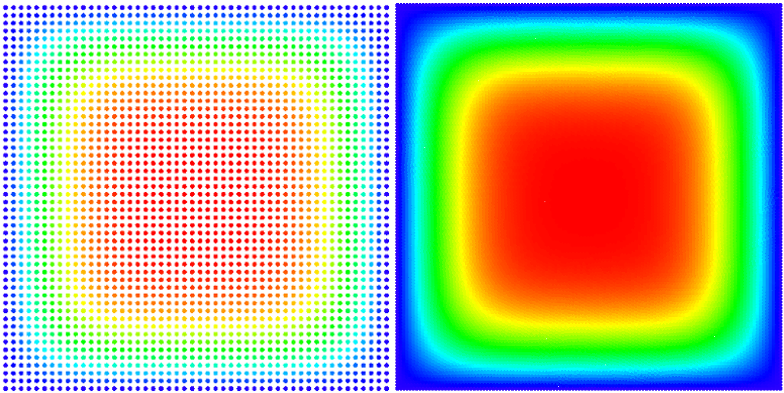
A picture of our solution (with smaller and larger node density):
Contents
Analysis of our method
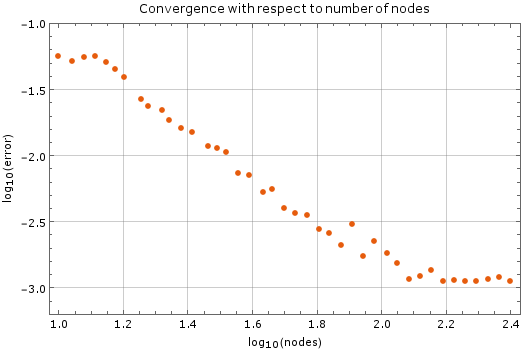
Convergence with respect to number of nodes
We tested the method with a fixed time step of $ \Delta t = 1\cdot 10^{-5}$ on a unit square ($a = 1$). Monomial basis of $6$ monomials was used and $12$ closest nodes counted as support for each node. After more than $250$ nodes of discretization in each dimension the method diverges, which is expected. The stability criterion for diffusion equation in two dimensions is $\Delta t \leq \frac{1}{4} \Delta x^2$, where $\Delta x$ is the spatial discretization step in one dimension. In our case, at $250$ nodes per side, the right hand side yields $\frac{1}{4}\cdot\frac{1}{250}\cdot\frac{1}{250} = 4\times 10^{-6}$, so our method is stable within the expected region.
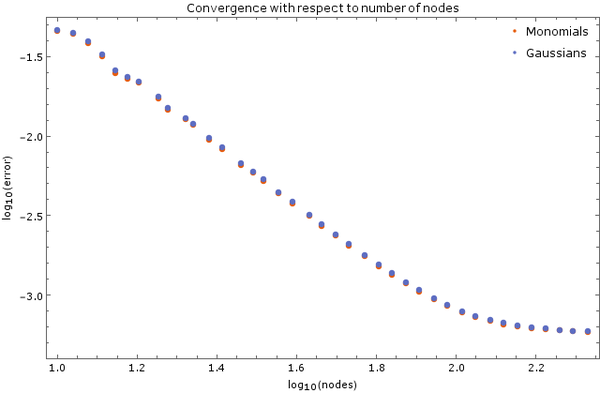
Above is another image of convergence, this time using monomial basis $\{1, x, y, x^2, y^2\}$ and Gaussian basis with discretization step $ \Delta t = 5 \cdot 10^{-6}$ and 5 support nodes. Total node count was $N = 2500$. Error was calculated after $0.01$ time units have elapsed.
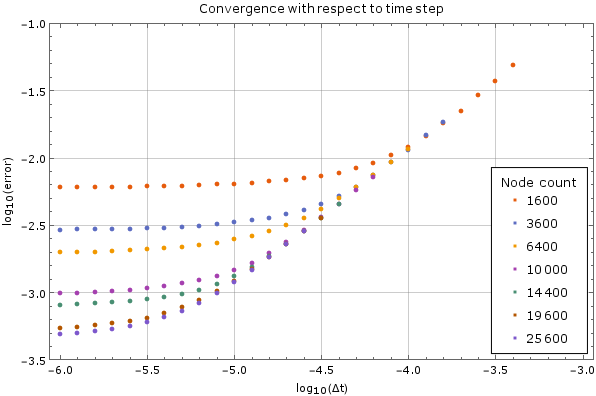
Convergence with respect to number of time steps
We tested the method on a fixed node count with different time steps on the same domain as above. For large time steps the method diverges, but once it starts converging the precision increases steadily as the time step decreases, until it hits its lower limit. This behaviour is expected. The error was calculated against the analytical solution above after $0.005$ units of time have passed. A monomial basis up to order $2$ inclusive ($m = 6$) was used and the support size was $n = 12$.
Using Gaussian basis
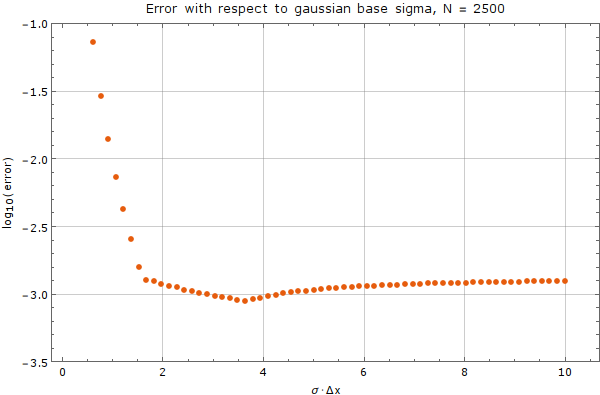
We tested the method on a fixed node count of $N = 2500$ with spatial step discretization of $\Delta x = \frac{1}{50}$. We used the Gaussian basis of $m = 5$ functions with support size $n = 13$. Error was calculated against analytical solution above after $0.01$ time units. A time step of $\Delta t = 10^{-5}$ was used.
As we can see from the graph, there exists an interval where the choice of $\sigma$ does not matter much, but outside of this interval, the method diverges rapidly. Care from the user side must be taken, to choose $\sigma$ appropriately, with respect to plot above.
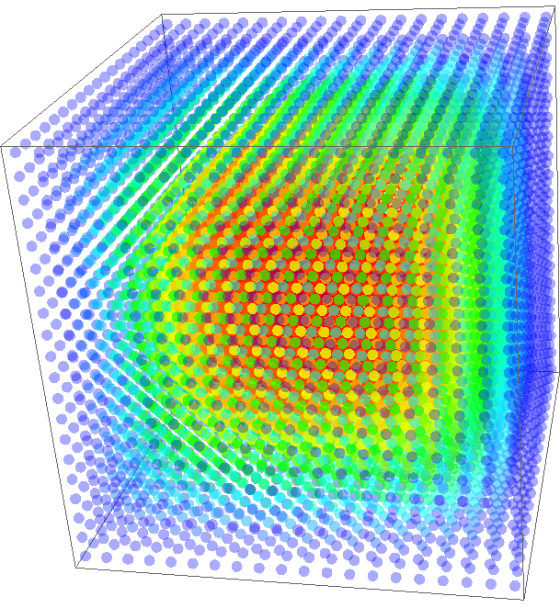
Solving in 3D
A 3-dimensional case on domain $[0, 1]^3$ was tested on $N = 20^3$ nodes, making the discretization step $\Delta x = 0.05$. Support size of $n=10$ with $m=10$ Gaussian basis functions was used. Their normalization parameter was $\sigma = 60\Delta x$. A time step of $\Delta t = 10^{-5}$ and an explicit Euler method was used to calculate the solution of to $0.01$ time units.
Solving Dirichlet with EngineMLS
Example code using explicit stepping to reproduce the thermal images from the beginning: example code
Solving Dirichlet with MLSM operators
Example code using explicit stepping and MLSM operators to reproduce the thermal images from the beginning:example code
Solving mixed boundary conditions with MLSM operators
By using MLSM operators and utilizing its `MLSM::neumann` method we can also solve partial diffusion equations.
Example code showing the use of Neumann boundary conditions:[]
@snippet mlsm_operators_test.cpp Quarter diffusion example
We also support more – interesting – domains :)
@image html mikimouse_heat.png @image latex mikimouse_heat.png