Difference between revisions of "Hertzian contact"
(→FreeFem++ numerical solution) |
(→FreeFem++ numerical solution) |
||
| Line 91: | Line 91: | ||
*Coefficient of friction: $\mu = 0.85$ | *Coefficient of friction: $\mu = 0.85$ | ||
*Cylinder radius: $R = 50$ mm | *Cylinder radius: $R = 50$ mm | ||
| − | *Specimen length: $L = $ | + | *Specimen length: $L = 40$ mm |
| − | *Specimen | + | *Specimen height: $H = 5$ mm |
| + | |||
| + | We assume that both the pad and specimen are from the same material, therefore the combined modulus is \[E^* = \frac{E}{2(1-\nu^2)}.\] | ||
=References= | =References= | ||
<references/> | <references/> | ||
Revision as of 11:06, 21 November 2016
Click on Solid Mechanics to go back.
Contents
Contact of Cylinders - the Hertz problem
Detailed discussions of this problem can be found in Hills and Nowells (1994) as well as Williams and Dwyer-Joyce (2001). [1] [2]
If two circular cylinders with radii $R_1$ and $R_2$ are pressed together by a force per unit length of magnitude $P$ with their axes parallel, then the contact patch will be of half-width $b$ such that \begin{equation} b = \sqrt{\frac{2PR}{\pi E^*}} \end{equation} where $R$ and $E^*$ are the reduced radius of contact and the contact modulus defined by \begin{equation} \frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2}, \end{equation} \begin{equation} \frac{1}{E^*} = \frac{1-{\nu_1}^2}{E_1} + \frac{1-{\nu_2}^2}{E_2}. \end{equation}
The resulting pressure distribution $p(x)$ is semielliptical, i.e., of the form \begin{equation} p(x) = p_0 \sqrt{1-\frac{x^2}{b^2}} \end{equation} where the peak pressure \begin{equation} p_0 = \sqrt{\frac{PE^*}{\pi R}}. \end{equation}
The coordinate $x$ is measured perpendicular to that of the cylinder axes. For the case of nominal contact between cylinders closed form analytical solutions are available.
The surfaces stresses are given by the equations:
The surface stresses and stresses along the line of symmetry are shown in the following two graphs. The $x$ and $z$ coordinates are normalized with the contact width $b$.
Contact of cylinders under partial slip
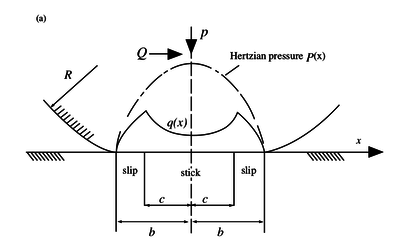
The second case we study is the application of a tangential force $Q$ to the previous problem. When the tangential force is less than the limiting force of friction, i.e., \[|Q| < \mu P,\] where $\mu$ is the coefficent of friction, sliding motion will not occur but the contact will be divided into regions of slip and stick zones that are unknown a priori. For the case of cylinders the analysis is given in Hills & Nowell (1994), p. 44.
Besides the normal traction $p(x)$ we know have an additional shear traction given by \begin{equation} q(x) = \begin{cases} -\mu p_0 \sqrt{1 - \frac{x^2}{b^2}}, \quad c \leq |x| \leq b \\ -\mu p_0 \left(\sqrt{1 - \frac{x^2}{b^2}} - \frac{c}{b}\sqrt{1 - \frac{x^2}{c^2}}\right), \quad |x| < c \end{cases} \end{equation} where $b$ is the half-width of the whole contact, and $c$ the half-width of the central sticking region. The width of the central zone, i.e. the value of dimension $c$ is dependent on the applied tangential force $Q$: \begin{equation} \frac{c}{b} = \sqrt{1 - \frac{Q}{\mu P}} \end{equation}
The distributions $q(x)$ and $p(x)$ as well as the widths of the stick and slip zones can be seen in the image below.
The effect of bulk stress
Additionally we might be interested in the addition of bulk stress. This type of stress occurs in fretting fatique experiments like the one shown below.
The previous solution for contact of cylinders under partial slip can be adjusted for the presence of bulk stresses $\sigma_\mathrm{axial}$. These cause an eccentricity $e$ to the solution given above. The shear traction $q(x)$ can be written as: \begin{equation} q(x) = \begin{cases} -\mu p_0 \sqrt{1 - \frac{x^2}{b^2}}, \quad c \leq | x - e | \text{ and } |x| \leq b \\ -\mu p_0 \left[\sqrt{1 - \frac{x^2}{b^2}} - \frac{c}{b}\sqrt{1 - \frac{(x-e)^2}{c^2}}\right], \quad |x-e| < c \end{cases} \end{equation} where once again \[ \frac{c}{b} = \sqrt{1 - \frac{Q}{\mu P}}\] and \begin{equation} e = \frac{b \sigma_\mathrm{axial}}{4 \mu p_0}. \end{equation} If larger values of $\sigma_\mathrm{axial}$ are applied, one edge of the stick zone will approach the edge of the contact ($e$ becomes larger). The solution for the shear stress traction is therefore only valid if $e + c \leq b$, i. e. \[\frac{\sigma_\mathrm{axial}}{\mu p_0} \leq 4\left(1 - \sqrt{1 - \frac{Q}{\mu P}}\right).\]
FreeFem++ numerical solution
For the numerical solution in FreeFem++ we choose parameters equal to those in Pereira et al. (2016): [3]
- Modulus of elasticity: $E = 72.1$ GPa
- Poisson's ratio: $\nu = 0.33$
- Normal load: $P = 1234$ N
- Tangential load: $Q = 155.165$ N
- Axial stress: $\sigma_\mathrm{axial} = 100$ MPa
- Coefficient of friction: $\mu = 0.85$
- Cylinder radius: $R = 50$ mm
- Specimen length: $L = 40$ mm
- Specimen height: $H = 5$ mm
We assume that both the pad and specimen are from the same material, therefore the combined modulus is \[E^* = \frac{E}{2(1-\nu^2)}.\]
References
- ↑ Hills, D. A. and Nowell, D. (1994). Mechanics of Fretting Fatique, p. 20-25. Springer Science+Business Media, Dordrecht.
- ↑ Williams, John A. and Dwyer-Joyce, Rob S. (2001). Contact Between Solid Surfaces, p. 121 in Modern Tribology Handbook: Volume 1, Principles of Tribology, editor: Bushan, Bharat. CRC Press LLC, Boca Raton.
- ↑ Pereira et al. (2016). On the convergence of stresses in fretting fatique. Materials, 9, 639.