Revision as of 15:48, 15 November 2016 (view source) Ipribec (talk | contribs) (→‎FreeFem++) ← Older edit		Revision as of 15:56, 15 November 2016 (view source) Ipribec (talk | contribs) (→‎Numerical solution) Newer edit →
Line 56:		Line 56:
	* Young's modulus: $E = 3 \times 10^7$ N/m<sup>2</sup>		* Young's modulus: $E = 3 \times 10^7$ N/m<sup>2</sup>
	* Poisson's ratio: $\nu = 0.3$		* Poisson's ratio: $\nu = 0.3$
−	* Height of the beam: $D = 12$ m	+	* Depth of the beam: $D = 12$ m
	* Length of the beam: $L = 48$ m		* Length of the beam: $L = 48$ m

---

Revision as of 15:56, 15 November 2016

Do you want to go back to Solid Mechanics?

On this page we conduct numerical studies of bending of a cantilever loaded at the end, a common numerical benchmark in elastostatics. ^[1]

Exact solution

The exact solution to this problem is given by Timoshenko (1951) where it is derived for plane stress conditions. ^[2] Consider a beam of dimensions $L \times D$ having a narrow rectangular cross section. The origin of the coordinate system is placed at $(x,y) = (0,D/2)$. The beam is bent by a force $P$ applied at the end $x = 0$ and the other end of the beam is fixed (at $x = L$). The stresses in such a beam are given as:

$$\begin{equation} \sigma_{xx} = -\frac{Pxy}{I}, \end{equation}$$ $$\begin{equation} \sigma_{yy} = 0, \end{equation}$$ $$\begin{equation}\label{eq:sxy} \sigma_{xy} = -\frac{P}{2I}\left(\frac{D^2}{4} - y^2 \right), \end{equation}$$ where $I = D^3/12$ is the moment of inertia.

The exact solution in terms of the displacements in $x$- and $y-$ direction is

$$\begin{align}\label{eq:beam_a1} u_x(x,y) &= -\frac{Py}{6EI}\left(3(x^2-L^2) -(2+\nu)y^2 + 6 (1+\nu) \frac{D^2}{4}\right) \\ \label{eq:beam_a2} u_y(x,y) &= \frac{P}{6EI}\left(3\nu x y^2 + x^3 - 3L^2 x + 2L^3\right) \end{align}$$ where $E$ is Young's modulus and $\nu$ is the Poisson ratio.

Alternatively we may prefer to see the force applied on the right side at $x = L$, and have the left end at $(x,y) = (0,0)$ fixed. In this case the solution can be found in the following expandable section.

Numerical solution

For the numerical solution we first choose the following parameters: ^[3]

• Loading: $P = -1000$ N
• Young's modulus: $E = 3 \times 10^7$ N/m²
• Poisson's ratio: $\nu = 0.3$
• Depth of the beam: $D = 12$ m
• Length of the beam: $L = 48$ m

The unloaded beam is discretized with $40 \times 10$ regular nodes. Since the right end of the beam at $x = L$ is fixed, the displacement boundary conditions are prescribed from the known analytical formulae ($\ref{eq:beam_a1}$) and ($\ref{eq:beam_a2}$) :

$$\begin{equation} u_x(L,y) = -\frac{P}{6EI}\left(-(2+\nu)y^2 + 6 (1+\nu) \frac{D^2}{4}\right); \qquad u_y(L,y) = \frac{P}{2EI}(\nu L y^2) \end{equation}$$ The traction boundary at the left end of the beam ($x=0$) is given by ($\ref{eq:sxy}$): $$\begin{equation}\label{eq:trac_a} t_y(L,y) = -\frac{P}{2I}\left(\left(\frac{D}{2}\right)^2 - y^2 \right). \end{equation}$$

An indicator of the accuracy that can be employed is the strain energy error $e$:

$$\begin{equation} e = \left[ \frac{1}{2} \int_\Omega (\b{\varepsilon}^\mathrm{num} - \b{\varepsilon}^\mathrm{exact})\b{C}(\b{\varepsilon}^\mathrm{num} - \b{\varepsilon}^\mathrm{exact}) d\Omega\right]^{1/2} \end{equation}$$ where $\b{\varepsilon}$ is the strain tensor in vector form, $\b{C}$ the reduced stiffness tensor (a matrix) and $\Omega$ the domain of the calculated solution.

FreeFem++

The required code to solve this problem in FreeFem++ is:

// Parameters
real E = 3.0e7, nu = 0.3;
real P = -1000;
real L = 48, D = 12;
real I = D^3/12;

// Mesh
mesh Th = square(40,10,[L*x,-D/2+D*y]);

// Macros
macro u [ux,uy] // displacement
macro v [vx,vy] // test function
macro div(u) (dx(u[0])+dy(u[1])) // divergence
macro eM(u) [dx(u[0]), dy(u[1]), sqrt(2)*(dx(u[1]) + dy(u[0]))/2] // strain tensor

// Finite element space
fespace Vh(Th,[P2,P2]);
Vh u, v;

// Boundary conditions
func uxb = -P*y/(6*E*I)*(nu*y^2-2*(1+nu)*y^2+6*D^2/4*(1+nu));
func uyb = P/(6*E*I)*(3*nu*L*y^2);
func ty = -P/(2*I)*(D^2/4-y^2);

// Convert E and nu to plane stress
E = E/(1-nu^2); nu = nu/(1-nu);

// Lame parameters
real mu = E/(2*(1+nu));
real lambda = E*nu/((1+nu)*(1-2*nu));

// Solve problem
solve cantileverBeam(u,v) =
   int2d(Th)(lambda*div(u)*div(v) + 2*mu*(eM(u)'*eM(v)))
   - int1d(Th,4)([0,-ty]'*v)
   + on(2,ux=uxb,uy=uyb);

// Plot solution
real coef = 1000;
Th = movemesh(Th,[x+ux*coef,y+uy*coef]);
plot(Th,wait=1);

The numerical solutions for beam displacements $u_y(x,0)$ in the axial direction of the beam, and shear stresses $\sigma_{xy}(L/2,y)$ in a cross section at the half lengthwise of the beam, obtained by quadratic finite elements are shown in the figure below. Analytic solutions are shown with continuous lines.

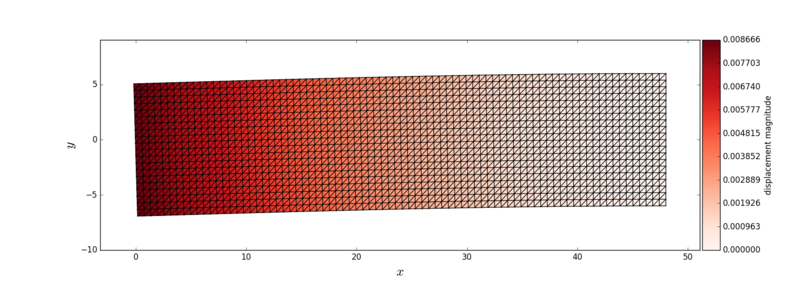
The displaced mesh coloured with the value of the displacement magnitude is presented in the following figure. The displacements are magnified by a factor of 10.

References

1. Jump up ↑ Augarde, Charles E. and Deeks, Andrew J.. "The use of Timoshenko's exact solution for a cantilever beam in adaptive analysis" , Finite Elements in Analysis and Design. (2008), doi: 10.1016/j.finel.2008.01.010
2. Jump up ↑ Timoshenko, S. and Goodier, J. N. (1951). Theory of elasticity, p. 35 - 39. McGraw-Hill, Inc., New York.
3. Jump up ↑ Liu, Gui-Rong (2003). Mesh free methods: moving beyond the finite element method, p. 161. CRC Press LLC, Boca Raton.