Difference between revisions of "Triple dielectric step in 1D"
| Line 1: | Line 1: | ||
| + | Back to [[Computational electromagnetics]]. | ||
| + | == Case == | ||
<math> | <math> | ||
\newcommand{\eps}{\varepsilon} | \newcommand{\eps}{\varepsilon} | ||
\newcommand{\dpar}[2]{\frac{\partial #1}{\partial #2}} | \newcommand{\dpar}[2]{\frac{\partial #1}{\partial #2}} | ||
</math> | </math> | ||
| − | |||
| − | |||
A good starting point in the study of computational electromagnetics is a calculation of reflectance and transmissivity of a simple device. In this example, we will be studying device made of three dielectric layers with different dielectric constants. The layers are infinite and thus the problem simplifies to one dimension. We still need to differentiate between two different cases, the incident wave can be either $y$ polarized | A good starting point in the study of computational electromagnetics is a calculation of reflectance and transmissivity of a simple device. In this example, we will be studying device made of three dielectric layers with different dielectric constants. The layers are infinite and thus the problem simplifies to one dimension. We still need to differentiate between two different cases, the incident wave can be either $y$ polarized | ||
\begin{equation} | \begin{equation} | ||
Revision as of 16:59, 11 August 2020
Back to Computational electromagnetics.
Case
\( \newcommand{\eps}{\varepsilon} \newcommand{\dpar}[2]{\frac{\partial #1}{\partial #2}} \) A good starting point in the study of computational electromagnetics is a calculation of reflectance and transmissivity of a simple device. In this example, we will be studying device made of three dielectric layers with different dielectric constants. The layers are infinite and thus the problem simplifies to one dimension. We still need to differentiate between two different cases, the incident wave can be either $y$ polarized \begin{equation} \dpar{H_z}{t} =- \frac{1}{\mu(r)}\dpar{E_y}{x}, \qquad \text{in} \qquad \dpar{E_y}{t} = -\frac{1}{\eps(r)}\dpar{H_z}{x}, \end{equation} or $z$ polarized \begin{equation} \dpar{H_y}{t} = \frac{1}{\mu(r)}\dpar{E_z}{x}, \qquad \text{in} \qquad \dpar{E_y}{t} = \frac{1}{\eps(r)}\dpar{H_y}{x}, \end{equation}
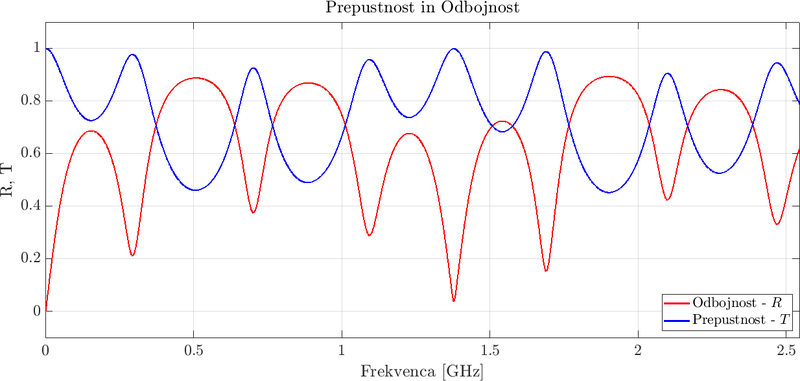
Results
The problem for $z$-polarized incident light was solved with the medusa library using $N = 4001$ points and $\Delta t = dx/2c_0$. The simulation used a TFSF source that was located at $x = 0.1$, a Gaussian source that contained frequencies up to 2.5GHz was used. The plots below show a single step during the simulation and the transmissivity and reflectance of the device.