Difference between revisions of "Parametric domains"
(→Variable node density and dirchlet boundary conditions in 2D) |
|||
| Line 1: | Line 1: | ||
Go back to [[Medusa#Examples|Examples]]. | Go back to [[Medusa#Examples|Examples]]. | ||
| − | == Variable node density and | + | == Variable node density and Dirichlet boundary conditions in 2D == |
| − | With | + | With Medusa, we can also solve partial differential equations on parametric domains. Consider the solution of a simple 2D Poisson equation with Dirichlet boundary conditions: |
<math> | <math> | ||
\begin{align*} | \begin{align*} | ||
Revision as of 18:15, 8 August 2019
Go back to Examples.
Variable node density and Dirichlet boundary conditions in 2D
With Medusa, we can also solve partial differential equations on parametric domains. Consider the solution of a simple 2D Poisson equation with Dirichlet boundary conditions\[ \begin{align*} \Delta u &= 0.5 &&\text{in } \Omega, \\ u &= 0 &&\text{on } \partial \Omega, \end{align*} \] Let's define $\Omega$ to be the interior of the parametrically given curve $r(t): [- 2 \pi, 0] \to \mathbb{R}^2$\[ \begin{align*} f(t) &= |\cos(-1.5 t)| ^ {\sin(-3t)} \\ r(t) &= (r \cos(-t), r \sin(-t)) \end{align*} \] Using tools such as Wolfram Mathematica, we can find the Jacobian matrix ($\textbf{J}$) of $r$. Now, we can translate the definition of $r$ into code:
1 auto example_r = [](Vec1d t) {
2 t(0) = -t(0);
3 double f = pow(abs(cos(1.5 * t(0))), sin(3 * t(0)));
4 return Vec2d(f * cos(t(0)), f * sin(t(0)));
5 };
6
7 auto der_example_r = [](Vec1d t) {
8 t(0) = -t(0);
9 double f = pow(abs(cos(1.5 * t(0))), sin(3 * t(0)));
10 double der_f = (-1.5 * pow(abs(cos(1.5 * t(0))),
11 sin(3 * t(0))) * sin(3 * t(0)) * sin(1.5 * t(0)) + 3 * pow(abs(cos(1.5 * t(0))),
12 sin(3 * t(0))) * cos(3 * t(0)) * cos(1.5 * t(0)) *
13 log(abs(cos(1.5 * t(0))))) / cos(1.5 * t(0));
14
15 Eigen::Matrix<double, 2, 1> jm;
16 jm.col(0) << -(der_f * cos(t(0)) - f * sin(t(0))), -(der_f * sin(t(0)) + f * cos(t(0)));
17
18 return jm;
19 };
20
21 // Define parametric curve's domain.
22 BoxShape<Vec1d> bs(Vec<double, 1>{- 2 * PI}, Vec<double, 1>{0.0});
23 DomainDiscretization<Vec1d> param_d(bs);
We implemented $r$ and $\textbf{J}$ as lambda expressions and $r$'s domain as an instance of DomainDiscretization class. Now we can fill the target domain with nodes given by $r$ and the density function $h$ by using GeneralSurfaceFill. For the sake of this example, we choose a gradient-like density function gradient_h.
1 UnknownShape<Vec2d> shape;
2 DomainDiscretization<Vec2d> domain(shape);
3
4 auto gradient_h = [](Vec2d p){
5 double h_0 = 0.005;
6 double h_m = 0.03 - h_0;
7
8 return (0.5 * h_m * (p(0) + p(1) + 3.0) + h_0) / 5.0;
9 };
10
11 GeneralSurfaceFill<Vec2d, Vec1d> gsf;
12 domain.fill(gsf, param_d, example_r, der_example_r, gradient_h);
After that, we can fill the interior of the domain in the usual way and choose the closest 9 nodes of each node as its support.
1 GeneralFill<Vec2d> gf;
2 domain.fill(gf, gradient_h);
3
4 int N = domain.size();
5 domain.findSupport(FindClosest(9));
Finally, we translate the partial differential equations of our problem into code and solve the problem, as in other examples.
1 int m = 2; // basis order
2 Monomials<Vec2d> mon(m);
3 RBFFD<Polyharmonic<double, 3>, Vec2d> approx({}, mon);
4
5 // Compute the shapes (we only need the Laplacian).
6 auto storage = domain.computeShapes<sh::lap>(approx);
7
8 Eigen::SparseMatrix<double, Eigen::RowMajor> M(N, N);
9 Eigen::VectorXd rhs(N); rhs.setZero();
10 M.reserve(storage.supportSizes());
11
12 // Construct implicit operators over our storage.
13 auto op = storage.implicitOperators(M, rhs);
14
15 for (int i : domain.interior()) {
16 op.lap(i) = 0.5; // set the case for nodes in the domain
17 }
18 for (int i : domain.boundary()) {
19 op.value(i) = 0.0; // enforce the boundary conditions
20 }
21
22 Eigen::BiCGSTAB<decltype(M), Eigen::IncompleteLUT<double>> solver;
23 solver.compute(M);
24 ScalarFieldd u = solver.solve(rhs);
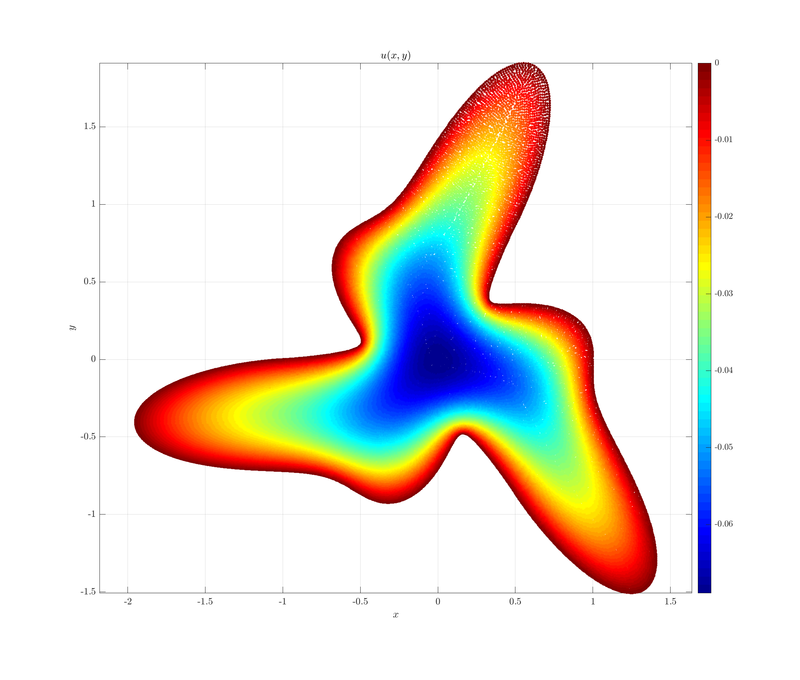
Here is the plot of $u(x, y)$.
The whole example can be found as parametric_domain_2D.cpp along with the plot script that can be run by Matlab or Octave parametric_domain_2D.m.
See Positioning of computational nodes (TODO) for the theory behind our node placing algorithm.