Difference between revisions of "Complex-valued problems"

Revision as of 15:08, 19 July 2019

Go back to Examples.

Our library natively supports complex numbers. To demonstrate this a tutorial for solving Poisson's equation is presented below. For more complicated complex-valued problems see Electromagnetic scattering and Schrödinger equation.

2D Complex Poisson's equation

We are solving 2D complex Poisson equation, on a unit square with Dirichlet boundary conditions

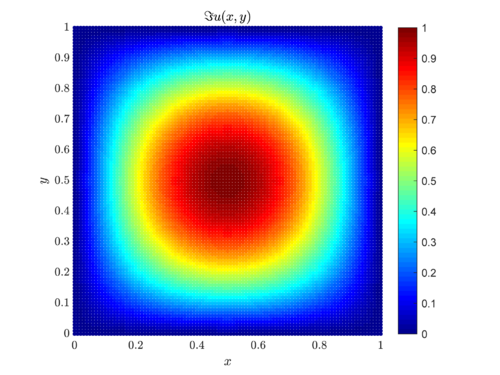
\[ \begin{align*} i \Delta u &= f &&\text{in } \Omega, \\ u &= 0 &&\text{on } \partial \Omega, \end{align*} \] where $u(x,y)$ is the solution to the problem and $\Omega = [0, 1] \times [0, 1]$ denotes the square domain. We will consider $f(x,y) = 2\pi^2\sin(\pi x)\sin(\pi y)$, as it makes for a simple solution $u(x,y) = i\sin(\pi x)\sin(\pi y)$.

We write the equations for our problem by directly translating the mathematical formulation above into code.

for (int i : domain.interior()) {
    double x = domain.pos(i, 0);
    double y = domain.pos(i, 1);
    1.0_i * op.lap(i) = 2*PI*PI*sin(PI * x)*sin(PI * y);
}
for (int i : domain.boundary()) {
    op.value(i) = 0.0;
}

The solution $u(x,y)$ is plotted below. In our case solution consist only of the imaginary part, the real part is equal to zero.

Go back to Examples.