Difference between revisions of "Natural convection in 3D irregular domain"
From Medusa: Coordinate Free Mehless Method implementation
| Line 3: | Line 3: | ||
for Ra$=10^6$ case in 3D are presented. A more quantitative analysis is done by comparing characteristic values, i.e.\ | for Ra$=10^6$ case in 3D are presented. A more quantitative analysis is done by comparing characteristic values, i.e.\ | ||
peak positions and values of cross section velocities, with data available in | peak positions and values of cross section velocities, with data available in | ||
| − | literature~\cite{ | + | literature~\cite{fusegi1991numerical}. We analyze six different cases, |
| − | |||
namely $\textup{Ra} = 10^6,10^7,10^8$ in 2D, and $\textup{Ra} = 10^4,10^5,10^6$ in 3D. | namely $\textup{Ra} = 10^6,10^7,10^8$ in 2D, and $\textup{Ra} = 10^4,10^5,10^6$ in 3D. | ||
The comparison in presented in~\cref{tab:ff-data}. | The comparison in presented in~\cref{tab:ff-data}. | ||
| − | |||
All spatial operators are discretized using RBF-FD with $r^3$ PHS radial basis | All spatial operators are discretized using RBF-FD with $r^3$ PHS radial basis | ||
| Line 16: | Line 14: | ||
boundary conditions are additionally treated with ghost nodes [[Ghost nodes (theory)]]. | boundary conditions are additionally treated with ghost nodes [[Ghost nodes (theory)]]. | ||
| − | [[File: | + | [[File:DVD_3D.png|400px]] |
| − | + | [[File:DVD_3D_irreg.png|400px]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Revision as of 15:27, 18 May 2019
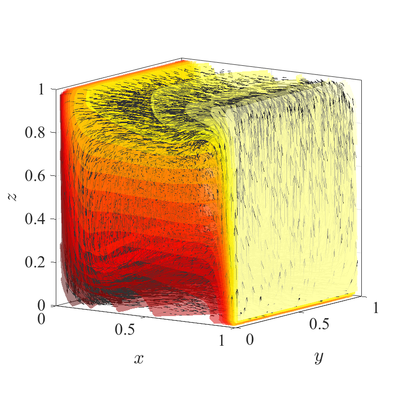
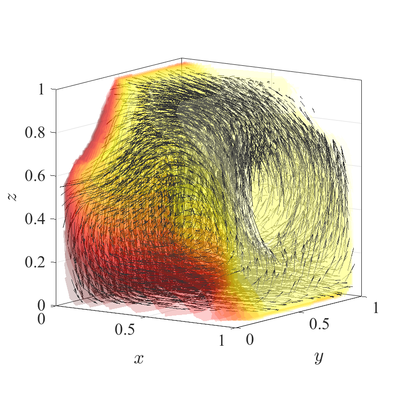
The classical De Vahl Davis natural convection test can be extended to 3D. In below figures steady state temperature contour and velocity quiver plots for Ra$=10^6$ case in 3D are presented. A more quantitative analysis is done by comparing characteristic values, i.e.\ peak positions and values of cross section velocities, with data available in literature~\cite{fusegi1991numerical}. We analyze six different cases, namely $\textup{Ra} = 10^6,10^7,10^8$ in 2D, and $\textup{Ra} = 10^4,10^5,10^6$ in 3D. The comparison in presented in~\cref{tab:ff-data}.
All spatial operators are discretized using RBF-FD with $r^3$ PHS radial basis functions, augmented with monomials up to order $2$, with the closest $25$ nodes used as a stencil. For the time discretization time step $\Delta t=10^{-3}$ was used for all cases. Nodal distance $h=0.01$ is used for simulations in 2D and $h=0.25$ for simulations in 3D. Boundaries with Neumann boundary conditions are additionally treated with ghost nodes Ghost nodes (theory).
