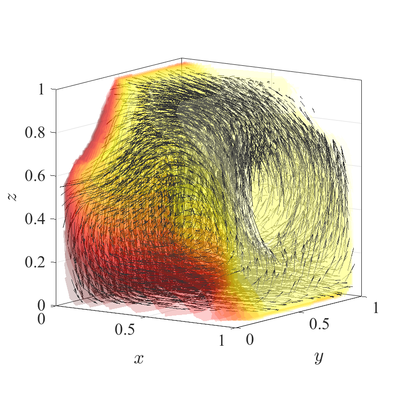
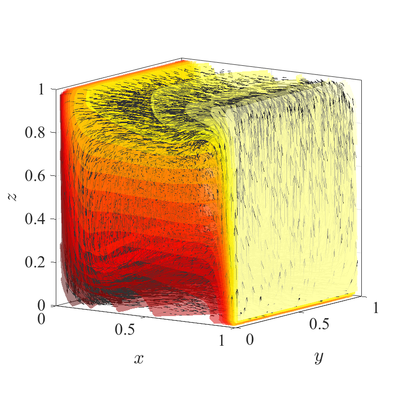
Difference between revisions of "Natural convection in 3D irregular domain"
From Medusa: Coordinate Free Mehless Method implementation
| Line 1: | Line 1: | ||
| − | + | The classical [[De Vahl Davis natural convection test]] can be extended to 3D | |
All spatial operators are discretized using RBF-FD with $r^3$ PHS radial basis | All spatial operators are discretized using RBF-FD with $r^3$ PHS radial basis | ||
functions, augmented with monomials up to order $2$, with the closest $25$ | functions, augmented with monomials up to order $2$, with the closest $25$ | ||
| Line 5: | Line 5: | ||
$\Delta t=10^{-3}$ was used for all cases. Nodal distance $h=0.01$ is used for | $\Delta t=10^{-3}$ was used for all cases. Nodal distance $h=0.01$ is used for | ||
simulations in 2D and $h=0.25$ for simulations in 3D. Boundaries with Neumann | simulations in 2D and $h=0.25$ for simulations in 3D. Boundaries with Neumann | ||
| − | boundary conditions are additionally treated with ghost nodes[[Ghost nodes (theory)]]. | + | boundary conditions are additionally treated with ghost nodes [[Ghost nodes (theory)]]. |
[[File:DVD_3D_irreg.png|400px]][[File:DVD_3D.png|400px]] | [[File:DVD_3D_irreg.png|400px]][[File:DVD_3D.png|400px]] | ||
Revision as of 15:21, 18 May 2019
The classical De Vahl Davis natural convection test can be extended to 3D All spatial operators are discretized using RBF-FD with $r^3$ PHS radial basis functions, augmented with monomials up to order $2$, with the closest $25$ nodes used as a stencil. For the time discretization time step $\Delta t=10^{-3}$ was used for all cases. Nodal distance $h=0.01$ is used for simulations in 2D and $h=0.25$ for simulations in 3D. Boundaries with Neumann boundary conditions are additionally treated with ghost nodes Ghost nodes (theory).