Difference between revisions of "Poisson's equation"
| Line 1: | Line 1: | ||
| − | It is fitting that examples start with the simplest case imaginable. So before we move on to more complex cases and interesting domains we will consider the solution of the Poisson equation on a unit square with Dirichlet boundary conditions: | + | It is fitting that examples start with the simplest case imaginable. So before we move on to more complex cases and interesting domains we will consider the solution of the 2D Poisson equation on a unit square with Dirichlet boundary conditions: |
| + | |||
| + | <math> | ||
| + | \begin{cases} | ||
| + | \Delta u = f(x,y) &\text{in } \Omega \\ | ||
| + | u = 0 &\text{on } \partial \Omega | ||
| + | \end{cases} | ||
| + | </math> | ||
| + | |||
| + | Where <math> u(x,y) </math> is the solution to the problem, <math> \Omega = [0, 1] \times [0, 1] </math> and in the case we will consider <math> f(x,y) = -2\pi^2sin(\pi x)sin(\pi y) </math>, as it makes for a simple solution <math> u(x,y) = sin(\pi x)sin(\pi y) </math>. | ||
| + | |||
| + | |||
| + | First of all, we must construct our domain and discretize it, then find support for each node. | ||
| + | |||
| + | <syntaxhighlight lang="c++" line> | ||
| + | BoxShape<Vec2d> box(0.0, 1.0); | ||
| + | double dx = 0.01; | ||
| + | DomainDiscretization<Vec2d> domain = box.discretizeWithStep(dx); | ||
| + | |||
| + | int N = domain.size(); | ||
| + | domain.findSupport(FindClosest(9)); | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | We constructed a box shape, discretized it with a constant step dx (both inside and the boundary) and choose the closest 9 nodes of each node as its support. The next very important step is to construct our approximation engine. Simply put approximation engines are classes responsible for [[Computation of shape functions|computing shape functions]] for given operator and points. While many different setups are supported in Medusa we will start off simple. | ||
| + | |||
| + | <syntaxhighlight lang="c++" line> | ||
| + | int m = 2 | ||
| + | WLS<Monomials<Vec2d>, NoWeight<Vec2d>, | ||
| + | ScaleToFarthest> wls(Monomials<Vec2d>::tensorBasis(m), {}); | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | We constructed a [[Moving Least Squares (MLS)| WLS]] using a monomial basis up to (inclusive) order 2 given with a tensor product. Finally, we translate the mathematical formulation of our problem into code. | ||
| + | |||
| + | <syntaxhighlight lang="c++" line> | ||
| + | for (int i : domain.interior()) { | ||
| + | double x = domain.pos(i,0); | ||
| + | double y = domain.pos(i,1); | ||
| + | op.lap(i) = -2*M_PI*M_PI*std::sin(M_PI*x)*std::sin(M_PI*y); | ||
| + | } | ||
| + | for (int i : domain.boundary()) { | ||
| + | op.value(i) = 0.0; | ||
| + | } | ||
| + | </syntaxhighlight> | ||
| + | |||
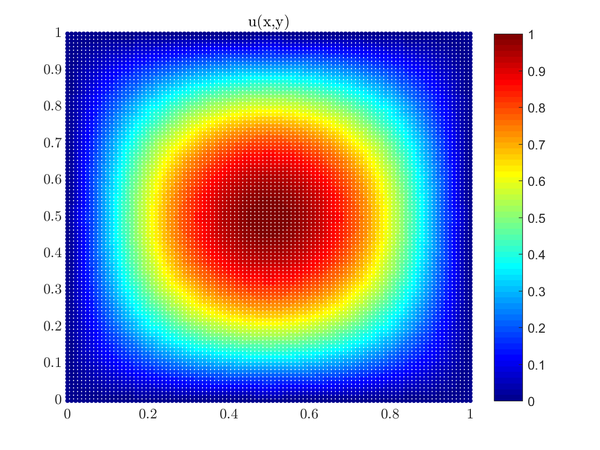
| + | Here is the plot of the solution for <math>u(x,y)</math> | ||
| + | |||
| + | |||
| + | [[File:solution_poisson2d_dirichlet_implicit.png|600px]] | ||
| + | |||
| + | The whole example can be found as [https://gitlab.com/e62Lab/medusa poisson_implicit_dirichlet_2D.cpp] along with the Matlab script [https://gitlab.com/e62Lab/medusa poisson_implicit_dirichlet_2D.m]. Same goes for similar cases solved in 1D and 3D and their respective Matlab scripts. | ||
Revision as of 11:23, 2 August 2018
It is fitting that examples start with the simplest case imaginable. So before we move on to more complex cases and interesting domains we will consider the solution of the 2D Poisson equation on a unit square with Dirichlet boundary conditions\[ \begin{cases} \Delta u = f(x,y) &\text{in } \Omega \\ u = 0 &\text{on } \partial \Omega \end{cases} \]
Where \( u(x,y) \) is the solution to the problem, \( \Omega = [0, 1] \times [0, 1] \) and in the case we will consider \( f(x,y) = -2\pi^2sin(\pi x)sin(\pi y) \), as it makes for a simple solution \( u(x,y) = sin(\pi x)sin(\pi y) \).
First of all, we must construct our domain and discretize it, then find support for each node.
1 BoxShape<Vec2d> box(0.0, 1.0);
2 double dx = 0.01;
3 DomainDiscretization<Vec2d> domain = box.discretizeWithStep(dx);
4
5 int N = domain.size();
6 domain.findSupport(FindClosest(9));
We constructed a box shape, discretized it with a constant step dx (both inside and the boundary) and choose the closest 9 nodes of each node as its support. The next very important step is to construct our approximation engine. Simply put approximation engines are classes responsible for computing shape functions for given operator and points. While many different setups are supported in Medusa we will start off simple.
1 int m = 2
2 WLS<Monomials<Vec2d>, NoWeight<Vec2d>,
3 ScaleToFarthest> wls(Monomials<Vec2d>::tensorBasis(m), {});
We constructed a WLS using a monomial basis up to (inclusive) order 2 given with a tensor product. Finally, we translate the mathematical formulation of our problem into code.
1 for (int i : domain.interior()) {
2 double x = domain.pos(i,0);
3 double y = domain.pos(i,1);
4 op.lap(i) = -2*M_PI*M_PI*std::sin(M_PI*x)*std::sin(M_PI*y);
5 }
6 for (int i : domain.boundary()) {
7 op.value(i) = 0.0;
8 }
Here is the plot of the solution for \(u(x,y)\)
The whole example can be found as poisson_implicit_dirichlet_2D.cpp along with the Matlab script poisson_implicit_dirichlet_2D.m. Same goes for similar cases solved in 1D and 3D and their respective Matlab scripts.