Difference between revisions of "Convection Diffusion equation"
(→Boring 1D case) |
(→Boring 1D case) |
||
| Line 53: | Line 53: | ||
FDM, it can be seen that the execution times for FDM and MLSM | FDM, it can be seen that the execution times for FDM and MLSM | ||
are the same for all practical purposes. | are the same for all practical purposes. | ||
| + | |||
| + | = Time dependent 2D case | ||
| + | We solved the equation on a square $\Omega = [0, a] \times [0, a]$ with | ||
| + | Dirichlet boundary conditions $ \left. u\right|_{\partial \Omega} = 0 $ and | ||
| + | initial state $ u(t = 0) = 1$. An analytical solution for this domain is known | ||
| + | \begin{equation} | ||
| + | u(\vec{p}, t) = \sum_{\substack{n=1 \\ n \text{ | ||
| + | odd}}}^\infty\sum_{\substack{m=1 \\ m \text{ odd}}}^\infty \frac{1}{\pi^2} | ||
| + | \frac{16 a^2}{nm} \sin\left(\frac{\pi n}{a}p_x\right) \sin\left(\frac{\pi | ||
| + | m}{a}p_y\right) e^{-\frac{\pi^2 (n^2+m^2)}{a^2}t} | ||
| + | \end{equation} | ||
| + | Because the solution is | ||
| + | given in the series form, we only compare to the finite approximation, summing | ||
| + | to $N = 100$ instead of infinity. Solution is on <xr id="fig:square_heat"/>. | ||
| + | See the code for solving diffusion [https://gitlab.com/e62Lab/e62numcodes/blob/master/examples/diffusion/diffusion.cpp here]. | ||
| + | |||
| + | <figure id="fig:square_heat"> | ||
| + | [[File:square_heat.png|thumb|upright=2|center|alt=A square of nodes coloured according to the solution(with smaller and larger node density)|<caption>A picture of our solution (with smaller and larger node density)</caption>]] | ||
| + | </figure> | ||
| + | |||
| + | ==Convergence with respect to number of nodes== | ||
| + | |||
| + | <figure id="fig:node_convergence"> | ||
| + | [[File:node_convergence.png|thumb|upright=2|center|alt=Graph of errors with respect to number of nodes|<caption>Convergence with respect to number of nodes</caption>]] | ||
| + | </figure> | ||
| + | |||
| + | We tested the method with a fixed time step of $ \Delta t = 1\cdot 10^{-5}$ | ||
| + | on a unit square ($a = 1$). Results are on <xr id="fig:node_convergence"/>. Monomial basis of $6$ monomials was used and $12$ | ||
| + | closest nodes counted as support for each node. After more than $250$ nodes of | ||
| + | discretization in each dimension the method diverges, which is expected. The | ||
| + | stability criterion for diffusion equation in two dimensions is $\Delta t \leq | ||
| + | \frac{1}{4} \Delta x^2$, where $\Delta x$ is the spatial discretization | ||
| + | step in one dimension. In our case, at $250$ nodes per side, the right hand side | ||
| + | yields $\frac{1}{4}\cdot\frac{1}{250}\cdot\frac{1}{250} = 4\times 10^{-6}$, | ||
| + | so our method is stable within the expected region. | ||
| + | |||
| + | <figure id="fig:node_convergence_5"> | ||
| + | [[File:node_convergence_5.png|thumb|upright=2|center|<caption>Convergence with respect to number of nodes for Gaussian and Monomial basis</caption>]] | ||
| + | </figure> | ||
| + | |||
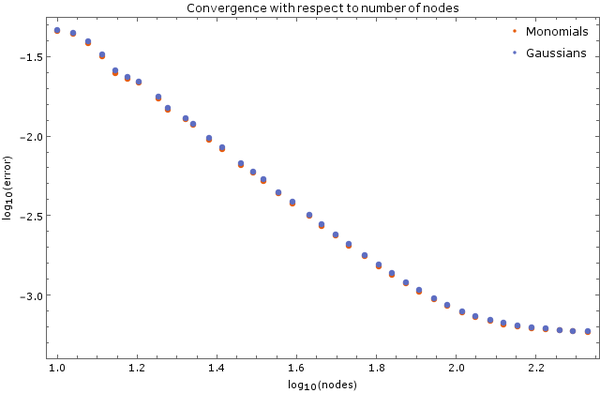
| + | On <xr id="fig:node_convergence_5"/> is another image of convergence, this time using monomial basis $\{1, x, | ||
| + | y, x^2, y^2\}$ and Gaussian basis with discretization step $ \Delta t = 5 | ||
| + | \cdot 10^{-6}$ and 5 support nodes. Total node count was $N = 2500$. | ||
| + | Error was calculated after $0.01$ time units have elapsed. | ||
| + | |||
| + | <figure id="fig:node_convergence_comparison"> | ||
| + | [[File:explicit_implicit_diffusion_comparison_ver2.png|thumb|upright=2|center|<caption>Convergence with respect to number of nodes for explicit and implicit mixed boundary condition (Neumann is enforced in two different ways).</caption>]] | ||
| + | </figure> | ||
| + | |||
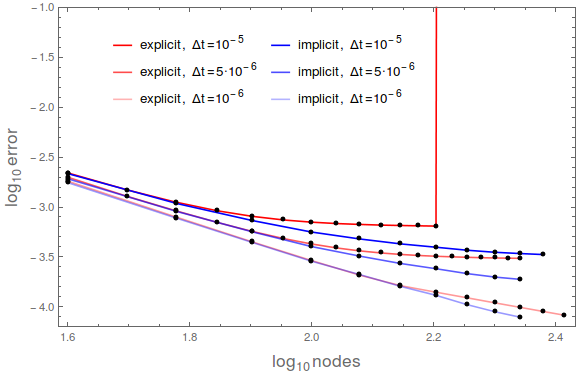
| + | Figure 4 shows convergence of 1/4 of the whole solution with Dirichlet boundary conditions (Fig. 1). The nodes were spanning the area $[0, a/2]^2$. As expected, higher number of nodes yields lower max error up to some maximal number of nodes. The latter is lower for explicit than for implicit method. | ||
| + | ==Convergence with respect to number of time steps== | ||
| + | <figure id="fig:timestep_convergence"> | ||
| + | [[File:timestep_convergence.png|thumb|upright=2|center|<caption>Convergence with respect to different timesteps</caption>]] | ||
| + | </figure> | ||
| + | |||
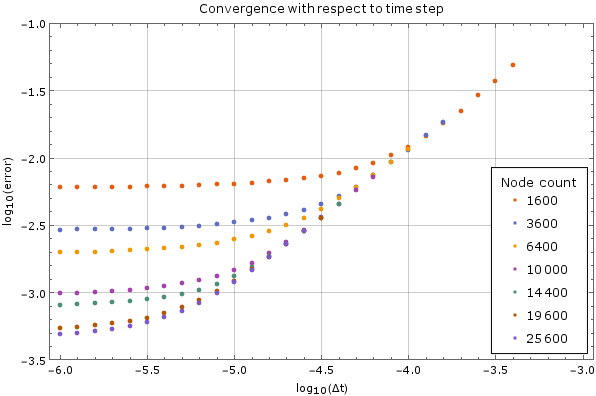
| + | We tested the method on a fixed node count with different time steps on the same | ||
| + | domain as above. Results are on <xr id="fig:timestep_convergence"/>. For large time steps the method diverges, but once it starts | ||
| + | converging the precision increases steadily as the time step decreases, until it | ||
| + | hits its lower limit. This behaviour is expected. The error was calculated | ||
| + | against the analytical solution above after $0.005$ units of time have passed. A | ||
| + | monomial basis up to order $2$ inclusive ($m = 6$) was used and the support | ||
| + | size was $n = 12$. | ||
Revision as of 11:24, 24 February 2018
Before moving to more complex numerical examples, preliminary tests are done on a case with a known closed form solution. As in all the previous examples, we use the diffusion equation for a test case. The main purpose of this section is basic evaluation of mesh based against meshless methods, as well as strong form against weak form methods. More specific analyses and performance tests are presented in Chapter \ref{cases}.
\section{Diffusion equation}
\index{Diffusion equation} A 2D diffusion equation in its dimensionless form is considered: \begin{align} %??? brezdimenzijska oblika nima c \frac{\partial u}{\partial t} - \nabla^2u = q, & \qquad (x, y)\in \Omega, \label{eq.diffu}\\ % \frac{\partial u(x,y,t)}{\partial t} = \nabla^2 u(x,y,t), & \qquad (x, y)\in \Omega, \label{eq.diffusion}\\ u(x,y,t) = \overline{u}(x,y,t), & \qquad (x,y) \in \Gamma_D,\label{eq.bc_diffu}\\ u(x,y,t),_n = \overline{g}(x,y,t), & \qquad (x,y) \in \Gamma_N, \label{eq.mixed.bc_diffu}\\ u(x,y,t) = u_0, & \qquad t=0,\label{eq.ic_diffu} \end{align} where $(x,y)$ are spatial coordinates, $t$ is time, $u(x, y, t)$ is the unknown solution, $ \Omega$, and $ \Gamma_D$ and $ \Gamma_N$ are the global domain with Dirichlet boundary and Neumann boundary, $\overline{u}$ and $\overline{g}$ are the prescribed Dirichlet and Neumann boundary values and $u(x,y,0)=u_0$ is the known initial condition.
Boring 1D case
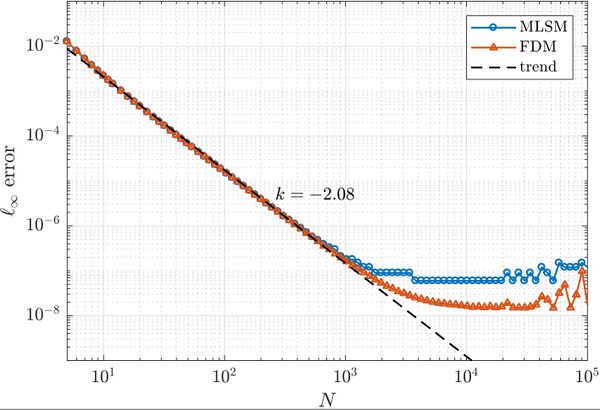
First, a simple one dimensional case is tackled to assess basic properties of presented solution method. Consider the problem \begin{align} u''(x) &= \sin(x), \quad x \in (0, 1) \nonumber \\ u(0) &= 0 \label{eq:neu1d} \\ u'(1) &= 0 \nonumber \end{align} with analytical solution \begin{equation} u(x) = x \cos 1 - \sin x. \end{equation} We solve the problem with MLSM using 3 support nodes and 3 monomials $\{1, x, x^2\}$ as basis functions on a regularly distributed nodes. This setup of MLSM is theoretically equivalent to the Finite Difference Method (FDM) and therefore it is worth implementing also standard FDM to compare results and execution times. The error between the actual solution $u$ and the approximate solution $\hat{u}$ is measured in $\ell_\infty$ norm, \begin{equation} \|u - \hat{u}\|_{\ell_\infty} = \max_{x\in X} | u(x) - \hat{u}(x)|, \label{eq:linf-err} \end{equation} where $X$ is the set of all points in the domain. The problem can be solved with below code.
1 for (int i : domain.internal()) {
2 op.lap(M, i, 1.0); // Equation.
3 rhs(i) = std::sin(domain.positions[i][0]);
4 }
5 op.value(M, left, 1.0); // Left BC.
6 op.neumann(M, right, {1}, 1.0); // Right BC.
7 VectorXd solution = M.lu().solve(rhs);
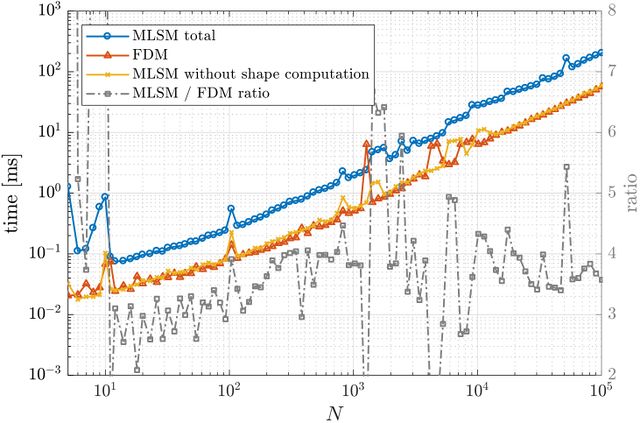
As expected, MLSM is slower due to computation of shape functions, which are known in advance in FDM. However, counting that as part of the preprocessing and measuring only the part equivalent to FDM, it can be seen that the execution times for FDM and MLSM are the same for all practical purposes.
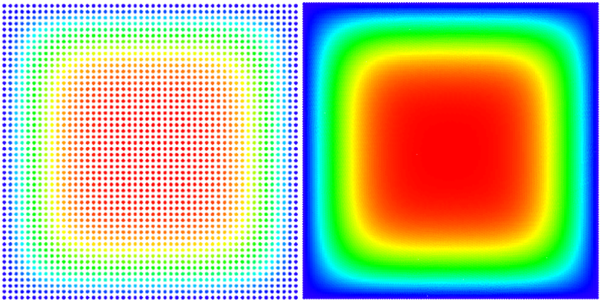
= Time dependent 2D case We solved the equation on a square $\Omega = [0, a] \times [0, a]$ with Dirichlet boundary conditions $ \left. u\right|_{\partial \Omega} = 0 $ and initial state $ u(t = 0) = 1$. An analytical solution for this domain is known \begin{equation} u(\vec{p}, t) = \sum_{\substack{n=1 \\ n \text{ odd}}}^\infty\sum_{\substack{m=1 \\ m \text{ odd}}}^\infty \frac{1}{\pi^2} \frac{16 a^2}{nm} \sin\left(\frac{\pi n}{a}p_x\right) \sin\left(\frac{\pi m}{a}p_y\right) e^{-\frac{\pi^2 (n^2+m^2)}{a^2}t} \end{equation} Because the solution is given in the series form, we only compare to the finite approximation, summing to $N = 100$ instead of infinity. Solution is on Figure 1. See the code for solving diffusion here.
Convergence with respect to number of nodes
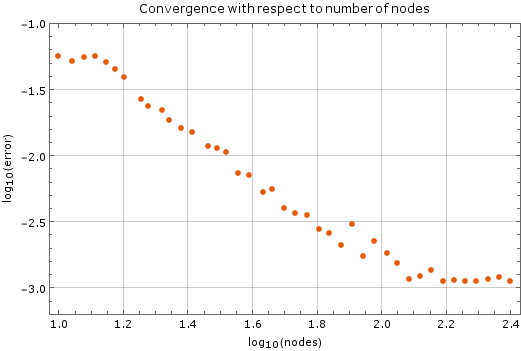
We tested the method with a fixed time step of $ \Delta t = 1\cdot 10^{-5}$ on a unit square ($a = 1$). Results are on Figure 2. Monomial basis of $6$ monomials was used and $12$ closest nodes counted as support for each node. After more than $250$ nodes of discretization in each dimension the method diverges, which is expected. The stability criterion for diffusion equation in two dimensions is $\Delta t \leq \frac{1}{4} \Delta x^2$, where $\Delta x$ is the spatial discretization step in one dimension. In our case, at $250$ nodes per side, the right hand side yields $\frac{1}{4}\cdot\frac{1}{250}\cdot\frac{1}{250} = 4\times 10^{-6}$, so our method is stable within the expected region.
On Figure 3 is another image of convergence, this time using monomial basis $\{1, x, y, x^2, y^2\}$ and Gaussian basis with discretization step $ \Delta t = 5 \cdot 10^{-6}$ and 5 support nodes. Total node count was $N = 2500$. Error was calculated after $0.01$ time units have elapsed.
Figure 4 shows convergence of 1/4 of the whole solution with Dirichlet boundary conditions (Fig. 1). The nodes were spanning the area $[0, a/2]^2$. As expected, higher number of nodes yields lower max error up to some maximal number of nodes. The latter is lower for explicit than for implicit method.
Convergence with respect to number of time steps
We tested the method on a fixed node count with different time steps on the same domain as above. Results are on Figure 5. For large time steps the method diverges, but once it starts converging the precision increases steadily as the time step decreases, until it hits its lower limit. This behaviour is expected. The error was calculated against the analytical solution above after $0.005$ units of time have passed. A monomial basis up to order $2$ inclusive ($m = 6$) was used and the support size was $n = 12$.